2. Ранг матрицы

Ранг данной матрицы есть такое число, что по крайней мере один определитель- го порядка, получаемый из этой матрицы при удалении некоторых строк и/или столбцов, отличен от нуля, а все определители- го порядка равны нулю.

Ранг матрицы равен наибольшему числу ее линейно независимых строк (или столбцов).

Для квадратной матрицы порядкаее рангудовлетворяет соотношению. Эта матрица является невырожденной в том и только в том случае, если ее ранг, т. е.. Если же, то матрица является вырожденной.

Ранг суммы двух матриц 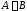не больше суммы их рангов:

.

Пример. Найти ранг матрицы .

◄ Ранг этой квадратной матрицы порядка удовлетворяет соотношению. Единственный определитель 3-го порядка, получаемый из этой матрицы. Ранг данной матрицы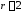, т. к. по крайней мере один определитель 2-го порядка, получаемый из этой матрицы при удалении 3-й строки и 3-го столбца,. ►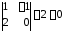

Пример. Найти ранг матрицы .

◄ Ранг этой матрицы , т. к. из данной матрицы можно получить определители порядка не выше 2-го. Легко убедиться, что все три определителя 2-го порядка, которые можно получить из этой матрицы удалением поочередно его столбцов, равны нулю. Отсюда следует, что ранг данной матрицы(каждый элемент матриц представляет собой определитель 1-го порядка). Уменьшение ранга этой матрицы по отношению к максимально возможномуобусловлено тем, что у нее строки и столбцы линейно зависимы (второй и третий столбец получаются из соответствующих элементов первого их умножением на 2 и 3, соответственно; вторая строка получается из первой, умножением ее элементов на 3). ►

В общем случае для вычисления ранга матрицы ее сначала приводят к более простому виду с помощью так называемых элементарных преобразований, к которым относятся:

1. перестановка строк матрицы;

2. умножение какой-либо строки на одно и то же отличное от нуля число;

3. прибавление к элементам строки соответствующих элементов другой строки, предварительно умноженных на некоторое число.

Можно показать, что элементарные преобразования не меняют ранга матрицы.

Если с помощью элементарных преобразований получить нули ниже главной диагонали матрицы, то ранг исходной матрицы будет равен числу ненулевых строк преобразованной матрицы.

Пример. С помощью элементарных преобразований вычислить ранг матрицы

.

◄ Умножим первую строку матрицы на –2 и прибавим ко второй строке:

~~.

Теперь умножим первую строку на –3 и сложим ее с третьей строкой, а затем вычтем из последней строки первую. Имеем

~~.

Умножая вторую строку получившейся матрицы на –2 и складывая ее с третьей строкой, а затем, складывая вторую строку с последней, получим матрицу

~.

Преобразованная матрица имеет две ненулевые строки, следовательно, ранг матрицы А равен двум: . ►

3. Обратная матрица

Квадратная матрица называетсяневырожденной, если она имеет (необходимо единственную) обратную матрицу , определяемую условиями

.

В противном случае матрица –вырожденная.

Квадратная матрица =() порядкаявляется невырожденной в том и только в том случае, если ее определитель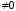; в этом случае обратная матрицаесть квадратная матрица того же порядка:

, (1.1.1)

где – алгебраические дополнения элементовв определителе.

Квадратная матрица не вырождена в том и только том случае, если ее строки (столбцы) линейно независимы. Строки (столбцы) матрицы линейно независимы, если ни одна строка (столбец) не могут быть выражены в виде линейной комбинации остальных строк (столбцов). В противном случае строки (столбцы) линейно зависимы.

Если матрицы ине вырождены и число, то

, ,.

Пример. Дана матрица . Найти обратную матрицу.

◄ Находим определитель матрицы . Т. к., делаем вывод, что матрица не вырождена и, следовательно, имеет обратную матрицу. Находим алгебраические дополнения для элементов матрицы:

, ,,

, ,,

, ,.

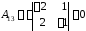Следовательно, по формуле (1.1.1)

.

Проводим проверку полученного результата:

. Делаем вывод, что результат правильный. ►