Тема 2 Определители и их свойства.

Лекция 1.2.1 «Определители и их свойства. Обратная матрица»

Учебные вопросы:

1. Определители и их свойства

2. Ранг матрицы

3. Обратная матрица

1. Определители и их свойства

Определителем (детерминантом) квадратной матрицы

называется число, обозначаемое символически

.

Число естьпорядок определителя.

Определитель 2-го порядка вычисляется по правилу

.

Пример. .

Определители 3-го и более высокого порядка вычисляются на основе их разложения по строке или столбцу на определители более низкого порядка при использовании общих свойств определителей.

Свойства определителей:

1. Величина определителя не меняется при замене строк столбцами и столбцов строками с теми же номерами;

2. Перестановка двух каких-либо строк (столбцов) равносильна умножению определителя на – 1;

3. Определитель, у которого элементы одной строки (или столбца) пропорциональны соответствующим элементам другой строки (столбца), равен нулю. В частности, определитель с двумя одинаковыми строками (столбцами) равен нулю.

Пример., т. к. элементы 3-го столбца пропорциональны соответствующим элементам 2-го с коэффициентом пропорциональности – 3.

4. Если элементы какой-либо строки (столбца) определителя равны нулю, то он равен нулю.

Пример. .

5. Общий множитель всех элементов какой-либо строки или столбца можно вынести за знак определителя.

Пример. .

6. Если элементы некоторого столбца (или строки) есть сумма двух слагаемых, то определитель равен сумме двух определителей, у которых элементы рассматриваемого столбца (строки) равны соответствующим слагаемым.

Пример. .

7. Если ко всем элементам какого-либо столбца (строки) прибавить слагаемые, пропорциональные соответствующим элементам другого столбца (строки), то величина определителя не изменится.

Пример. (к элементам 1-го столбца прибавлены соответствующие элементы 2-го, умноженные на 2.

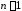Минор элементав определителе-го порядка есть определитель ()-го порядка, получающийся из данного определителя, если из него вычеркнуть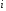-ю строку и-й столбец.

Пример. Для определителя минор элементаесть, а элемента—.

Алгебраическое дополнение 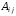элементаесть

=,

т. е. равно минору этого элемента, взятому со знаком «+», если сумма номеров строки и столбца, на пересечении которых он стоит, есть четное число, и знаком «–», если число нечетное.

Пример. Для определителя алгебраическое дополнение элементаесть, а элемента—.

Теорема о разложении определителя по строке или столбцу. Определитель равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения.

Вычисление определителя на основе теоремы о разложении облегчается, если выбирается стока (или столбец), содержащие нули. Используя свойство 7), можно преобразовать данный определитель так, чтобы все элементы (кроме одного) какой-либо строки (или столбца) стали нулями. Разлагая затем определитель по этой строке (столбцу), сразу уменьшаем его порядок на единицу.

Пример. Вычислить определитель .

◄ Разлагаем определитель по 3-му столбцу (через чередование знаков, начиная с верхнего левого элемента, верхними правыми индексами проставлены знаки алгебраических дополнений для элементов этого столбца): .

Разлагая данный определитель по второй строке, получаем тот же результат:

=. ►

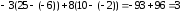Пример. Вычислить определитель .

◄ Используем свойство определителей 7). Умножая все элементы 2-й строки последовательно на (–2), (–3) и 2 и прибавляя их затем соответственно к элементам 1-й, 3-й и 4-й строки, получим: == (умножаем элементы 1-й строки последовательно на (–2) и (–11) и прибавляем их затем соответственно к элементам 2-й и 3-й строки) =

= . ►