
- •Конспект лекций
- •2. Основные операции над матрицами
- •Тема 2 Определители и их свойства.
- •1. Определители и их свойства
- •2. Ранг матрицы
- •3. Обратная матрица
- •Тема 3. Элементы линейной алгебры в экономике
- •1. Линейная модель международной торговли
- •2. Модель Леонтьева многоотраслевой экономики
- •Тема 4 Системы линейных алгебраических уравнений
- •1. Системы линейных алгебраических уравнений. Теорема Кронекера Капелли
- •2. Применение определителей к исследованию и решению систем линейных уравнений. Формулы Крамера
- •1. Решение систем линейных алгебраических уравнений методом обратной матрицы
- •2. Решение систем линейных алгебраических уравнений методом Гаусса
- •Тема 5 Элементы векторной алгебры
- •1. Векторы. Координаты вектора
- •2. Линейные операции над векторами
- •3. Скалярное и векторное произведение векторов
- •Тема 6. Элементы высшей алгебры
- •Тема 7 Элементы аналитической геометрии
- •1. Уравнение линии на плоскости
- •2. Прямая линия на плоскости
- •3. Полярные координаты
- •1. Канонические уравнения эллипса, гиперболы, параболы
- •2. Преобразования декартовой системы координат на плоскости
Институт экономики, управления и права (г. Казань)
Кафедра высшей математики
Конспект лекций
ПО КУРСУ ЛИНЕЙНОЙ АЛГЕБРЫ
Направление подготовки
080100.62 «Экономика»
Квалификация (степень) выпускника
Бакалавр
Набережные Челны 2013
Тема 1 Матрицы и операции над ними
Лекция 1.1.1 «Матрицы и операции над ними»
Учебные вопросы:
Матрицы, виды матриц
Основные операции над матрицами
1. Матрицы, виды матриц
Таблицу

называют
(прямоугольной)
матрицей размера
 .
Элементы
.
Элементы
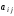 называютсяэлементами
матрицы;
элемент
называютсяэлементами
матрицы;
элемент
 расположен в
расположен в -йстроке
и в
-йстроке
и в
 -мстолбце
матрицы;
-мстолбце
матрицы;
 есть
число строк, а
есть
число строк, а –число
столбцов.
–число
столбцов.
Пример.
Матрица
 имеет размер
имеет размер ,
2 строки и 3 столбца.
,
2 строки и 3 столбца.
Если
в матрице число строк равняется числу
столбцов
 (матрица размера
(матрица размера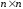 ),
то матрицу называют квадратной
матрицей порядка
),
то матрицу называют квадратной
матрицей порядка
 .
Квадратная матрица
.
Квадратная матрица
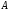 =(
=( )
называется:
)
называется:
симметричной
относительно главной диагонали,
если
 =
= ;
;
диагональной,
если
 =0
при
=0
при (все элементы, не стоящие на главной
диагонали, равны нулю);
(все элементы, не стоящие на главной
диагонали, равны нулю);
треугольной
(наддиагональной), если
 =0
при
=0
при (все
элементы, стоящие ниже главной диагонали,
равны нулю);
(все
элементы, стоящие ниже главной диагонали,
равны нулю);
строго
треугольной,
если
 =0
при
=0
при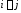 (все
элементы, стоящие на главной диагонали
и ниже ее, равны нулю).
(все
элементы, стоящие на главной диагонали
и ниже ее, равны нулю).
Пример.
Матрица

квадратная 3-го порядка; матрица
квадратная 3-го порядка; матрица
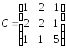 симметричная
относительно главной диагонали; матрица
симметричная
относительно главной диагонали; матрица

диагональная; матрица
диагональная; матрица

треугольная (наддиагональная); матрица
треугольная (наддиагональная); матрица
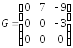
строго треугольная.
строго треугольная.
Единичной
матрицей
 называется диагональная матрица с
единичными диагональными элементами:
называется диагональная матрица с
единичными диагональными элементами:
 ,
где
,
где

Пример.
Матрица

единичная матрица 2-го порядка.
единичная матрица 2-го порядка.
Матрица
размера


называется
столбцом,
а матрица размера


– строчкой.
Нулевой
матрицей
 размера
размера называется матрица этого размера, все
элементы которой равны нулю.
называется матрица этого размера, все
элементы которой равны нулю.
Пример.
Матрица

нулевая матрица размера
нулевая матрица размера
 .
.
Матрицей,
транспонированной
по отношению к матрице
 =(
=( )
размера
)
размера ,
называется матрица
,
называется матрица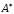 =(
=( )
размера
)
размера (столбцы матрицы
(столбцы матрицы являются строками матрицы
являются строками матрицы с теми же номерами).
с теми же номерами).
Пример.
Пусть
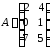 .
Транспонированной матрицей
.
Транспонированной матрицей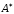 будет
будет
 .
.
2. Основные операции над матрицами
Две
матрицы
 =(
=( )
и
)
и =(
=( )равны
друг другу, если они одинакового размера
и их соответствующие элементы равны,
т. е.
)равны
друг другу, если они одинакового размера
и их соответствующие элементы равны,
т. е.
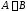 ,
,
если
 =
=
для
всех
 и
и .
.
Сумма
двух матриц
 =(
=( )
и
)
и =(
=( )
размера
)
размера есть матрица
есть матрица =(
=( )
размера
)
размера ,
у которой элементы являются суммой
соответствующих элементов матриц
слагаемых, т. е.
,
у которой элементы являются суммой
соответствующих элементов матриц
слагаемых, т. е.
 ,
,
если
 =
= +
+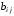
для
всех
 и
и .
.
Произведение
матрицы
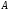 =(
=( )
размера
)
размера на число
на число
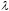 есть матрица
есть матрица
 размера
размера ,
у которой элементы равны соответствующим
элементам матрицы
,
у которой элементы равны соответствующим
элементам матрицы ,
умноженным на
,
умноженным на :
:

 =
= (
( )=(
)=(
 ).
).
Пример.
Даны матрицы
 и
и .
Найти матрицу
.
Найти матрицу .
.
◄
 =
=
 =
=
 =
=
=
 =
= .
►
.
►
Вычитание
матриц
 можно выполнять либо вычитанием
соответствующих элементов матриц, либо,
как в приведенном примере, через
прибавлениепротивоположной
матрицы –
можно выполнять либо вычитанием
соответствующих элементов матриц, либо,
как в приведенном примере, через
прибавлениепротивоположной
матрицы – (–
(–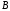
 ):
):
 =
= .
.
Произведение
матрицы
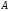 =(
=( )
размера
)
размера на матрицу
на матрицу
 =(
=(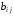 )размера
)размера
 есть матрица
есть матрица =(
=( )
размера
)
размера
 (
( )(
)( )
) (
( ),
),
где
 =
= .
.
Таким
образом, элемент
 матрицы
матрицы есть сумма произведений элементов
есть сумма произведений элементов -й
строки матрицы
-й
строки матрицы на соответствующие элементы
на соответствующие элементы -го
столбца матрицы
-го
столбца матрицы .
В каждом произведении матриц
.
В каждом произведении матриц форма
матриц
форма
матриц
 и
и должна быть
согласованной:
число столбцов
должна быть
согласованной:
число столбцов
 матрицы
матрицы должно равняться числу строк матрицы
должно равняться числу строк матрицы .
Из существования произведения
.
Из существования произведения вовсене
следует
существование произведения
вовсене
следует
существование произведения
 .Если
существуют оба произведения
.Если
существуют оба произведения и
и (это, в частности, будет всегда, если
(это, в частности, будет всегда, если и
и – квадратные матрицы одного порядка),
то, вообще говоря,
– квадратные матрицы одного порядка),
то, вообще говоря,

 .
.
Пример.
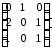
Даны матрицы
 и
и .
Найти
.
Найти .
.
◄
 =
=
 =
=
= =
= .
►
.
►
Для операций над матрицами справедливы следующие соотношения
( ,
,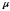 – числа,
– числа, ,
, ,
, – матрицы,
– матрицы, – единичная матрица):
– единичная матрица):
 ,
,  ,
,
 ,
,  ,
,
 ,
,  ,
,
 ,
,  ,
,

 (
( – квадратная матрица).
– квадратная матрица).
