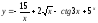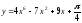- •Образец заполнения титульного листа домашней контрольной работы
- •Методические рекомендации по изучению курса
- •Общие методические указания по выполнению контрольной работы
- •Содержание тем контрольных работ
- •Требования к выполнению и оформлению контрольной работы
- •Вопросы для контроля теоретических знаний
- •1.2. Разложение определителя по элементам строки или столбца
- •1.3. Решение систем линейных уравнений методом определителей (метод Крамера)
- •II. Аналитическая геометрия
- •2.1. Координаты вектора в пространстве. Действия над векторами в координатной форме
- •2.2. Скалярное произведение векторов. Угол между векторами
- •2.3. Векторное произведение векторов
- •2.4. Общее уравнение плоскости
- •2.5. Общее уравнение прямой в пространстве
- •III. Введение в теорию пределов функций
- •Техника вычисления пределов
- •IV. Дифференциальное исчисление
- •4.1. Производная функции
- •4.2. Производные высших порядков функции
- •V. Интегральное исчисление
- •5.3.2. Метод замены переменной
- •5.4. Определенный интеграл и его свойства
- •5.5. Методы вычисления определенного интеграла
- •Задания для контрольной работы
5.3.2. Метод замены переменной
При нахождении интегралов вводится новая переменная, с помощью которой значительно упрощаются подынтегральные функции и интегралы принимают табличный вид. Определив интеграл по новой переменной, обратной подстановкой возвращаются к исходной переменной.
Пример 3.
Найти
интеграл
 .
.
Решение.
Интеграл
является нетабличным. Выполним замену
переменной:
 .Найдем
дифференциалы от левой и правой частей
равенства и выразим из негоxdx.
.Найдем
дифференциалы от левой и правой частей
равенства и выразим из негоxdx.

Таким образом, подынтегральная функция по переменной у имеет упрощенный вид, а интеграл сводится к табличному интегралу:

Возвращаясь к переменной х, имеем:

Следовательно:
 .
.
5.4. Определенный интеграл и его свойства
Пусть
функция y
= f(x)
определена на отрезке [a;
b].
Разобьем [a; b] на n равных частей точками: a = x0 < x1 < x2 <…< xn–1 < xn = b.
На
каждом элементарном отрезке [xi;
xi
+ 1]
выберем произвольную точку i
и обозначим
 .
.
Тогда
 называется интегральной суммой для
функцииf(x)
на отрезке [a;
b].
называется интегральной суммой для
функцииf(x)
на отрезке [a;
b].
Определенным
интегралом
от функции f(x)
на отрезке [a;
b]
называется предел интегральной суммы
функции при
 ,
стремящемся к нулю.
,
стремящемся к нулю.
Обозначение:

Основные свойства:

4. Если a < c < b, то

5.5. Методы вычисления определенного интеграла
1. Формула Ньютона — Лейбница:

Пример 4.
Вычислить
интеграл

Решение:
Согласно свойствам 1, 2, интеграл запишем в виде:

Применив формулу Ньютона — Лейбница, вычислим интегралы:


Следовательно, окончательно имеем

 .
.
2. Метод замены переменной.
Пример 5.
Вычислить
интеграл
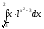
Решение:
При введении новой переменной у = х2 – 3 и определении подынтегральной функции по переменной у пределы интегрирования также будут изменяться.
Найдем пределы интегрирования по переменной у:
 –нижний
предел;
–нижний
предел;
 –верхний
предел;
–верхний
предел;
следовательно,

Применив формулу Ньютона — Лейбница, вычислим последний интеграл:

И,
значит,
 .
.
Пример 6.
Вычислить
 .
.
Решение:
Введем
переменную
 .
Дифференцируя обе части равенства и
выражаяx2dx,
будем иметь:
.
Дифференцируя обе части равенства и
выражаяx2dx,
будем иметь:

Найдем пределы интегрирования по переменной у:

Таким образом,
 .
.
Задания для контрольной работы
Вариант № 1
I. Теория определителей
1. Решить систему линейных уравнений:
а)
 б)
б)
II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
1) Найти:
а)
угол между векторами
 и
и ;
;
б)
площадь параллелограмма, построенного
на векторах
 и
и .
.
2) Составить уравнение плоскости, проходящей через точки A, B и C.
A(3; –1; 2), B(1; 1; 1), C(–5; 3; 1).
III. Теория пределов функции
3. Найти указанные пределы функций.
а)
 в)
в) б)
б) г)
г)
IV. Дифференциальное исчисление
4. Найти производные функций
 V.
Интегральное исчисление
V.
Интегральное исчисление
5. Вычислить неопределенный интеграл:
1.
 ;
2.
;
2. ;
;
Вариант № 2
I. Теория определителей
1. Решить систему линейных уравнений:
a)
 б)
б)
II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
1) Найти:
а)
угол между векторами
 и
и ;
;
б)
площадь параллелограмма, построенного
на векторах
 и
и .
.
2) Составить уравнение плоскости, проходящей через точки A, B и C.
A(1; 8; –3), B(3; 2; 6), C(2; 6; –1)
III. Теория пределов функции
3. Найти указанные пределы функций.
а)
 в)
в) б)
б) г)
г)
IV. Дифференциальное исчисление
Найти производные функций





V. Интегральное исчисление
5. Вычислить неопределенный интеграл:
.
 ;
2).
;
2). ;
;
Вариант № 3
I. Теория определителей
1. Решить систему линейных уравнений:
a)
 б)
б)
II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
1) Найти:
а)
угол между векторами
 и
и ;
;
б)
площадь параллелограмма, построенного
на векторах
 и
и .
.
2) Составить уравнение плоскости, проходящей через точки A, B и C.
A(4; –2; 5), B(2; 2; 1), C(3; 6; 1)
III. Теория пределов функции
3. Найти указанные пределы функций.
а)
 в)
в) б)
б) г)
г)
IV. Дифференциальное исчисление
4. Найти производные функций

V. Интегральное исчисление
5. Вычислить неопределенный интеграл:
.
 ;
б).
;
б). ;
;
ВАРИАНт № 4
I. Теория определителей
1. Решить систему линейных уравнений:
а)
 б)
б)
II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
1) Найти:
а)
угол между векторами
 и
и ;
;
б)
площадь параллелограмма, построенного
на векторах
 и
и .
.
2) Составить уравнение плоскости, проходящей через точки A, B и C.
A(–3; 7; 1), B(1; 5; 3), C(2; –7; 3)
III. Теория пределов функции
3. Найти указанные пределы функций.
а)
 в)
в) б)
б) г)
г)
IV. Дифференциальное исчисление
4. Найти производные функций

 сtg
сtg



V. Интегральное исчисление
5. Вычислить неопределенный интеграл:
 ;
б)
;
б)
 ;
;
Вариант № 5
I. Теория определителей
1. Решить систему линейных уравнений:
а)
 б)
б)
II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
1) Найти:
а)
угол между векторами
 и
и ;
;
б)
площадь параллелограмма, построенного
на векторах
 и
и .
.
2) Составить уравнение плоскости, проходящей через точки A, B и C.
A(2; 3; –6), B(5; –1; 6), C(4; 1; 3)
III. Теория пределов функции
3. Найти указанные пределы функций.
а)
 в)
в)
б)
 г)
г)
IV. Дифференциальное исчисление
4. Найти производные функций
V. Интегральное исчисление
5 Вычислить неопределенный интеграл:
А) ;
б)
;
б) ;
;
Вариант № 6
I. Теория определителей
1. Решить систему линейных уравнений:
а)
 б)
б)
II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
1) Найти:
а)
угол между векторами
 и
и ;
;
б)
площадь параллелограмма, построенного
на векторах
 и
и .
.
2) Составить уравнение плоскости, проходящей через точки A, B и C.
A(–1; 5; 4), B(5; –4; 2), C(1; 3; 3)
III. Теория пределов функции
3. Найти указанные пределы функций.
а)
 в)
в)
б)
 г)
г)
IV. Дифференциальное исчисление
4. Найти производные функций

V. Интегральное исчисление
5. Вычислить неопределенный интеграл:
А) ;
2.
;
2. ;
;
Вариант № 7
I. Теория определителей
1. Решить систему линейных уравнений:
а)
 б)
б)
II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
1) Найти:
а)
угол между векторами
 и
и ;
;
б)
площадь параллелограмма, построенного
на векторах
 и
и .
.
2) Составить уравнение плоскости, проходящей через точки A, B и C.
A(5; –2; 3), B(4; 6; –1), C(1; 2; 1)
III. Теория пределов функции
3. Найти указанные пределы функций.
а)
 в)
в) б)
б) г)
г)
IV. Дифференциальное исчисление
4. Найти производные функций
1

V. Интегральное исчисление
5. Вычислить неопределенный интеграл:
А).
 ;
б).
;
б). ;
;
Вариант № 8
I. Теория определителей
1. Решить систему линейных уравнений:
а)
 б)
б)
II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
1) Найти:
а)
угол между векторами
 и
и ;
;
б)
площадь параллелограмма, построенного
на векторах
 и
и .
.
2) Составить уравнение плоскости, проходящей через точки A, B и C.
A(8; –3; –1), B(4; –1; 3), C(–1; 3; 1)
III. Теория пределов функции
3. Найти указанные пределы функций.
а)
 в)
в) б)
б) г)
г)
IV. Дифференциальное исчисление
Найти производные функций





V. Интегральное исчисление
5. Вычислить неопределенный интеграл:
А) ;
б)
;
б) ;
;
Вариант № 9
I. Теория определителей
1. Решить систему линейных уравнений:
а)
 б)
б)
II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
1) Найти:
а)
угол между векторами
 и
и ;
;
б)
площадь параллелограмма, построенного
на векторах
 и
и .
.
2) Составить уравнение плоскости, проходящей через точки A, B и C.
A(–6; 1; 4), B(8; 3; –1), C(2; 5; 3)
III. Теория пределов функции
3. Найти указанные пределы функций.
а)
 в)
в) б)
б) г)
г)
IV. Дифференциальное исчисление
4. Найти производные функций

V. Интегральное исчисление
5. Вычислить неопределенный интеграл:
1.
 ;
2.
;
2. ;
;
Вариант № 10
I. Теория определителей
1. Решить систему линейных уравнений:
а)
 б)
б)
II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
1) Найти:
а)
угол между векторами
 и
и ;
;
б)
площадь параллелограмма, построенного
на векторах
 и
и .
.
2) Составить уравнение плоскости, проходящей через точки A, B и C.
A(–2; –4; 1), B(4; 5; 3), C(1; 8; 5)
III. Теория пределов функции
3. Найти указанные пределы функций.
а)
 в)
в) б)
б) г)
г)
IV. Дифференциальное исчисление
4. Найти производные функций
1

V. Интегральное исчисление
5. Вычислить неопределенный интеграл:
.
 ;
14.
;
14. ;
;
Вариант № 12
I. Теория определителей
1. Решить систему линейных уравнений:
а)
 б)
б)
. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
1) Найти:
а)
угол между векторами
 и
и ;
;
б)
площадь параллелограмма, построенного
на векторах
 и
и .
.
III. Теория пределов функции
3. Найти указанные пределы функций.
А)
 Б)
Б)
в)
 г)
г)

IV. Дифференциальное исчисление
4. Найдите производную функции:
V. Интегральное исчисление
5.Вычислить неопределенный интеграл
а)
 b)
b)

вариант № 11
I. Теория определителей
1. Решить систему линейных уравнений:
а
)
 б)
б)
Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
1) Найти:
а)
угол между векторами
 и
и ;
;
б)
площадь параллелограмма, построенного
на векторах
 и
и .
.
III. Теория пределов функции
А)
 ;6)
;6)
г)
 в)
в)
IV. Дифференциальное исчисление
4. Найдите производную функции:
V. Интегральное исчисление
5.Вычислить неопределенный интеграл
а)
 b)
b)

ВАРиант № 13
I. Теория определителей
1. Решить систему линейных уравнений:
а)
 б)
б)
. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
1) Найти:
) Найти:
а) угол между векторами
 и
и ;
;
б) площадь
параллелограмма, построенного на
векторах
 и
и .
.
III. Теория пределов функции
3. Найти указанные пределы функций.
А)
 ;
в)
;
в)

Б)
 г)
г)
IV. Дифференциальное исчисление
4. Найдите производную функции:
V. Интегральное исчисление
5.Вычислить неопределенный интеграл
а)
 b)
b)

Вариант № 14
I. Теория определителей
1. Решить систему линейных уравнений:
а)
 б)
б)
II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
1) Найти:
а) угол между векторами
 и
и ;
;
б) площадь
параллелограмма, построенного на
векторах
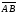 и
и .
.
2) Составить уравнение плоскости, проходящей через точки A, B и C.
A(1; 6; –3), B(3; 4; 6), C(2; 8; –1)
III. Теория пределов функции
3. Найти указанные пределы функций.
а)
 б)
б)

в)
 2)
2)

IV. Дифференциальное исчисление
Найдите производную функции:
V. Интегральное исчисление
5.Вычислить неопределенный интеграл
а)
 b)
b)
Вариант № 15
I. Теория определителей
1. Решить систему линейных уравнений:
А)
 б)
б)
II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
1) Найти:
а) угол между векторами
 и
и ;
;
б) площадь
параллелограмма, построенного на
векторах
 и
и .
.
2) Составить уравнение плоскости, проходящей через точки A, B и C.
A(1; 4; –3), B(3; 6; 6), C(2; 4; –1)
III. Теория пределов функции
3. Найти указанные пределы функций.
а)
 б)
б)

в)
 г)
г)
IV. Дифференциальное исчисление
Найдите производную функции:
1




V. Интегральное исчисление
5.Вычислить неопределенный интеграл
а)
 b)
b)

Вариант № 16
I. Теория определителей
1. Решить систему линейных уравнений:
а)
 б)
б)
II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
1) Найти:
а)
угол между векторами
 и
и ;
;
б)
площадь параллелограмма, построенного
на векторах
 и
и .
.
2) Составить уравнение плоскости, проходящей через точки A, B и C.
A(1; 2; –3), B(3; 4; 6), C(2; 2; –1)
III. Теория пределов функции
3. Найти указанные пределы функций.
а)
 б)
б)
г)
 в)
в)
IV. Дифференциальное исчисление
Найдите производную функции:





V. Интегральное исчисление
5.Вычислить неопределенный интеграл
a) b)
b)
Вариант №17
1 Теория определителей
1. Решить систему линейных уравнений:
а) б)
б)
II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
1) Найти:
а)
угол между векторами
 и
и ;
;
б)
площадь параллелограмма, построенного
на векторах
 и
и .
.
2) Составить уравнение плоскости, проходящей через точки A, B и C.
A(1; 8; –3), B(3; 2; 6), C(2; 6; –1)
III. Теория пределов функции
3. Найти указанные пределы функций.
а)
 6)
6)

в)
 г)
г)
IV. Дифференциальное исчисление
Найдите производную функции:
V. Интегральное исчисление
5.Вычислить неопределенный интеграл
a)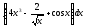 b)
b)
Вариант № 18
I. Теория определителей
1. Решить систему линейных уравнений:
а)
 б)
б)
II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
1) Найти:
а)
угол между векторами
 и
и ;
;
б)
площадь параллелограмма, построенного
на векторах
 и
и .
.
2) Составить уравнение плоскости, проходящей через точки A, B и C.
A(1; 8; –3), B(3; 2; 6), C(2; 6; –1)
III. Теория пределов функции
3. Найти указанные пределы функций.
а)
 б)
б)
в)
 г)
г)
IV. Дифференциальное исчисление
Найдите производную функции:

V. Интегральное исчисление
5.Вычислить неопределенный интеграл
. a) b)
b)
ВАриант № 19
I. Теория определителей
1. Решить систему линейных уравнений:
а)
 б)
б)
II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
1) Найти:
а)
угол между векторами
 и
и ;
;
б)
площадь параллелограмма, построенного
на векторах
 и
и .
.
2) Составить уравнение плоскости, проходящей через точки A, B и C.
A(1; 8; –3), B(3; 2; 6), C(2; 6; –1)
III. Теория пределов функции
3. Найти указанные пределы функций.
а)
 б)
б)
в)
 г)
г)
IV. Дифференциальное исчисление
Найдите производную функции:
V. Интегральное исчисление
5.Вычислить неопределенный интеграл
. а)
 b)
b)
ВАРИАНт № 20
I. Теория определителей
1. Решить систему линейных уравнений:
а)
 б)
б)
II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
1) Найти:
а)
угол между векторами
 и
и ;
;
б)
площадь параллелограмма, построенного
на векторах
 и
и .
.
2) Составить уравнение плоскости, проходящей через точки A, B и C.
A(1; 8; –3), B(3; 2; 6), C(2; 6; –1)
III. Теория пределов функции
3. Найти указанные пределы функций.
а)
 6)
6)

в)
 г)
г)
IV. Дифференциальное исчисление
Найдите производную функции:





V. Интегральное исчисление
5.Вычислить неопределенный интеграл
a) b)
b)
ВАриант № 21
I. Теория определителей
1. Решить систему линейных уравнений:
А
 б)
б)
II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
1) Найти:
а)
угол между векторами
 и
и ;
;
б)
площадь параллелограмма, построенного
на векторах
 и
и .
.
2) Составить уравнение плоскости, проходящей через точки A, B и C.
A(1; 8; –3), B(3; 2; 6), C(2; 6; –1)
III. Теория пределов функции
3. Найти указанные пределы функций.
а)
 б)
б)
в)
4)
 г)
г)
IV. Дифференциальное исчисление
Найдите производную функции:
1.
2.
3.
4.

 V.
Интегральное исчисление
V.
Интегральное исчисление
5.Вычислить неопределенный интеграл
a) b)
b)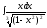
Вариант № 22
I. Теория определителей
1. Решить систему линейных уравнений:
а)
 б)
б)
II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
1) Найти:
а)
угол между векторами
 и
и ;
;
б)
площадь параллелограмма, построенного
на векторах
 и
и .
.
2) Составить уравнение плоскости, проходящей через точки A, B и C.
A(1; 8; –3), B(3; 2; 6), C(2; 6; –1)
III. Теория пределов функции
3. Найти указанные пределы функций.
а)
 б)
б)
в)
 г)
г)
IV. Дифференциальное исчисление
Найдите производную функции:
V. Интегральное исчисление
5.Вычислить неопределенный интеграл
a) b)
b)
Вариант № 23
I. Теория определителей
1. Решить систему линейных уравнений:
а)
 б)
б)
II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
1) Найти:
а)
угол между векторами
 и
и ;
;
б)
площадь параллелограмма, построенного
на векторах
 и
и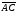 .
.
2) Составить уравнение плоскости, проходящей через точки A, B и C.
A(1; 8; –3), B(3; 2; 6), C(2; 6; –1)
III. Теория пределов функции
3. Найти указанные пределы функций.
а)
 б)
б)
в)
 г)
г)
IV. Дифференциальное исчисление
Найдите производную функции:





V. Интегральное исчисление
5.Вычислить неопределенный интеграл
. а)
 b)
b)
ВАриант № 24
I. Теория определителей
1. Решить систему линейных уравнений:
А) )б)
)б)
II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
1) Найти:
а)
угол между векторами
 и
и ;
;
б)
площадь параллелограмма, построенного
на векторах
 и
и .
.
2) Составить уравнение плоскости, проходящей через точки A, B и C.
A(1; 8; –3), B(3; 2; 6), C(2; 6; –1)
III. Теория пределов функции
3. Найти указанные пределы функций.
а)
 б)
б)
в)
 г)
г)
IV. Дифференциальное исчисление
Найдите производную функции:
V. Интегральное исчисление
5.Вычислить неопределенный интеграл
. а)
 b)
b)
Вариант № 25
I. Теория определителей
1. Решить систему линейных уравнений:
а)
 б)
б)
II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
1) Найти:
а)
угол между векторами
 и
и ;
;
б)
площадь параллелограмма, построенного
на векторах
 и
и .
.
2) Составить уравнение плоскости, проходящей через точки A, B и C.
A(1; 8; –3), B(3; 2; 6), C(2; 6; –1)
III. Теория пределов функции
3. Найти указанные пределы функций.
а)
 б)
б)
в)
 г)
г)
IV. Дифференциальное исчисление
Найдите производную функции:





V. Интегральное исчисление
5.Вычислить неопределенный интеграл
а)
 b)
b)
вариант № 26
I. Теория определителей
1. Решить систему линейных уравнений:
а)
 б )
б )
II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
1) Найти:
а)
угол между векторами
 и
и ;
;
б)
площадь параллелограмма, построенного
на векторах
 и
и .
.
2) Составить уравнение плоскости, проходящей через точки A, B и C.
A(1; 8; –3), B(3; 2; 6), C(2; 6; –1)
III. Теория пределов функции
3. Найти указанные пределы функций.
а)
 б)
б)
 в)
в) г)
г)

IV. Дифференциальное исчисление
4.Найдите производную функции:

V. Интегральное исчисление
5.Вычислить неопределенный интеграл
а)
 b)
b)
Вариант № 27
I. Теория определителей
1. Решить систему линейных уравнений:
а)
 б )
б )
II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
1) Найти:
а)
угол между векторами
 и
и ;
;
б)
площадь параллелограмма, построенного
на векторах
 и
и .
.
2) Составить уравнение плоскости, проходящей через точки A, B и C.
A(1; 8; –3), B(3; 2; 6), C(2; 6; –1)
III. Теория пределов функции
3. Найти указанные пределы функций.
а)
 б)
б)
в)
 г)
г)
IV. Дифференциальное исчисление
Найдите производную функции:





V. Интегральное исчисление
5.Вычислить неопределенный интеграл
а)
 b)
b)
Вариант № 28
I. Теория определителей
1. Решить систему линейных уравнений:
а)
 б )
б )
II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
1) Найти:
а)
угол между векторами
 и
и ;
;
б)
площадь параллелограмма, построенного
на векторах
 и
и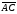 .
.
2) Составить уравнение плоскости, проходящей через точки A, B и C.
A(1; 8; –3), B(3; 2; 6), C(2; 6; –1)
III. Теория пределов функции
3. Найти указанные пределы функций.
а)
 б)
б)
в) г)4)
г)4)
IV. Дифференциальное исчисление
Найдите производную функции:
V. Интегральное исчисление
5.Вычислить неопределенный интеграл
. а)
 b)
b)
Вариант № 29
I. Теория определителей
1. Решить систему линейных уравнений:
а)
 б)
б)

II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
1) Найти:
а)
угол между векторами
 и
и ;
;
б)
площадь параллелограмма, построенного
на векторах
 и
и .
.
2) Составить уравнение плоскости, проходящей через точки A, B и C.
A(1; 8; –3), B(3; 2; 6), C(2; 6; –1)
III. Теория пределов функции
3. Найти указанные пределы функций.
а)
 б)
б)
в)
 г)
г)

IV. Дифференциальное исчисление
Найдите производную функции:
1.
2.
3.
4.
5.
V. Интегральное исчисление
5.Вычислить неопределенный интеграл
. а)
 b)
b)
Вариант № 30
I. Теория определителей
1. Решить систему линейных уравнений:
а)
 б)
б)
II. Аналитическая геометрия
2. Даны три точки: A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) в декартовой прямоугольной системе координат.
1) Найти:
а)
угол между векторами
 и
и ;
;
б)
площадь параллелограмма, построенного
на векторах
 и
и .
.
2) Составить уравнение плоскости, проходящей через точки A, B и C.
A(1; 8; –3), B(3; 2; 6), C(2; 6; –1)
III. Теория пределов функции
3. Найти указанные пределы функций.
а)
 б)
б)
в)
 г)
г)

IV. Дифференциальное исчисление
Найдите производную функции:
1.
2.
3.
4.


V. Интегральное исчисление
5.Вычислить неопределенный интеграл
а)
 b)
b)