Комплексное сопротивление элемента (участка цепи)

Под комплексным сопротивлением понимают отношения комплексной амплитуды входного напряжения к комплексной амплитуде входного тока:

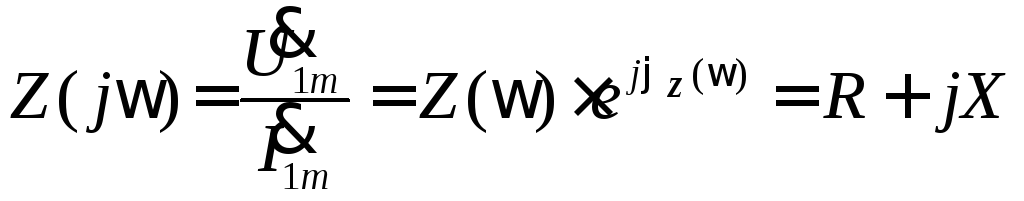. (1.6)

где Z –модуль комплексного сопротивления, φ=ψ_u - ψ_i – начальная фаза или аргумент комплексного сопротивления; R - активного сопротивления, X– реактивному сопротивлению, причем Z=(R²+X²)^1/2, а φ_z(ω)=ψ_u-ψ_i =arctg(X/R).

По виду записи комплексного сопротивления можно судить о характере участка цепи: Z=R – активное (резистивное) сопротивление; Z=R+jX — активно-индуктивное сопротивление; Z=R – j X — активно-емкостное

- комплексная проводимость, величина, обратная комплексному сопротивлению:

ПОСТРОЕНИЕ ВЕКТОРНЫХ ДИАГРАММ НА ВРАЩАЮЩЕЙСЯ КОМПЛЕКСНОЙ ПЛОСКОСТИ.

Для облегчения построения векторных диаграмм на вращающейся плоскости необходимо запомнить следующие основные положения:

а) В цепи с активным сопротивлениемток и напряжение совпадают по фазе.

б) В идеализированной цепи только с индуктивным сопротивлением без потерь напряжение по фазе опережает ток на угол, равный 90 градусов

в) В цепи с чисто емкостным сопротивлением без потерь ток опережает по фазе на­пряжение на угол +90 градусов.

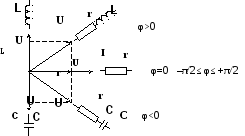
Рис.2.1.Мнемоническая схема, поясняющая возможные повороты радиусов-векторов при различном включении r-L-Cэлементов.

При построении векторных диаграмм надо начинать построение с вектора напряжения или тока общего для всей анализируемой цепи. В частности при последовательном включение элементов цепи надо начинать с построения вектора тока, протекающего через все элементы цепи. При параллельном включении элементов цепи построение векторной диаграммы надо начинать с вектора общего приложенного напряжения, а затем строить вектора токов, протекающих через каждую из ветвей электрической цепи. Возможные сдвиги фаз векторов напряжения в электрических цепях, состоящих из различных комбинаций r-L-C элементов, приведены на мнемонической схеме (см. рис.2.1.).

Радиус–вектора на схеме и ниже выделяются жирным шрифтом или точками (черточками) над ними.

Расчет цепей методом комплексных амплитуд

Метод комплексных амплитуд состоит в следующем:

1) исходная схема электрической цепи заменяется комплексной схемой замещения, в которой:

а) все пассивные элементы заменяются их комплексными сопротивлениями, как показано на рис. 4.27.

б) все токи и напряжения в схеме заменяются их комплексными амплитудами, т.е.х(t) =X_m cos(₀t – _x) X_m =X_m e^–jx.

R

Z_R=R

C

Z_C=1/(jC)

L

Z_L=jL

Рис. 4.27

2) Расчет электрической цепи сводится к составлению уравнений состояния цепи на основе законов Ома и Кирхгофа в комплексной форме и нахождениюкомплексных амплитуд токов или напряжений на интересующих нас участках цепи, т.е.Y_m = Y_m e^–jy.

3) Запись окончательного решения состоит в замене рассчитанных комплексных амплитуд на гармонические функции времени, т.е.

Y_m=Y_m e ^–jy  y(t) =Y_m cos(₀t – _y).

Пример 1. Алгоритм метода рассмотрим на примере анализа цепи, схема которой приведена на рис. 4.29.

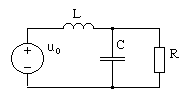
Рис. 4.29. RLC-цепь второго порядка

На вход цепи подается синусоидальное воздействие . Параметры воздействия и элементов цепи известны:U_m=1 В, ω =1 с^-1 , φ _u=90⁰ , R=1 Ом, L=1 Гн, C=1 Ф. Требуется определить токи и напряжения ветвей, построить векторную диаграмму.

Решение.

1. Представим воздействие в комплексной форме:

.

2. Построим схему замещения цепи в частотной области, заменив элементы цепи комплексными двухполюсниками, как это показано на рис. 4.30.

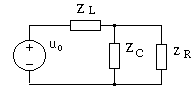
Рис. 4.30. Схема замещения цепи в частотной области

3. Произведем расчет реакций (токов и напряжений) в комплексной области. При этом можно воспользоваться законами Кирхгофа и Ома в комплексной форме, а также известными методами расчета резистивных цепей:

, ,,

,

, ,

,

, .

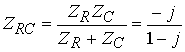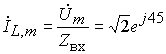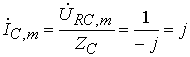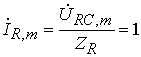3. Построим векторную диаграмму для токов и напряжений в цепи. Для этого на комплексной плоскости откладываются в соответствующем масштабе найденные токи и напряжения, как показано на рис. 4.31.

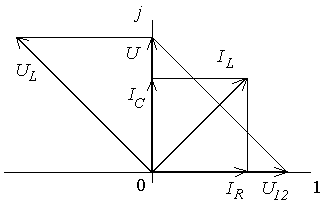
Рис. 4.31. Векторная диаграмма

 Построение векторной диаграммы, как правило, является конечным результатом решения подобных задач. Векторная диаграмма показывает амплитуду и начальную фазу любого тока или напряжения. При необходимости записать временную функцию тока или напряжения, это всегда можно сделать, имея векторную диаграмму. Например, напряжение на L-элементе имеет амплитуду , а начальную фазу 135⁰, значит, во временной области это напряжение можно записать так:

.

Пример 2. Задана эквивалентная схема цепи синусоидального тока (рис. 10) и ее параметры.

Рис. 10.

Выполнить следующие действия:

1. Рассчитать токи в ветвях и напряжения на элементах схемы;

2. Составить и проверить баланс полных, активных и реактивных мощностей;

3. Построить векторную диаграмму токов для узла а.

Расчет проводим символическим методом в следующем порядке:

1. Рассчитываем сопротивление всех элементов схемы (учитываем, что )

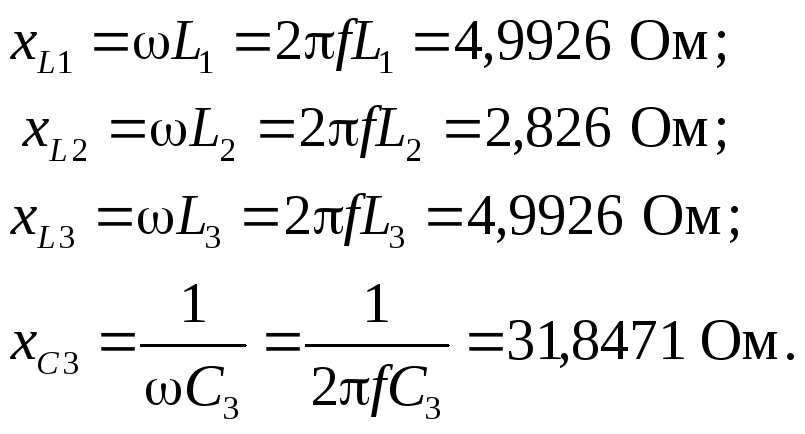
2. Представляем ЭДС источника в виде комплекса действующего значения. Определяем комплексные сопротивления и проводимости ветвей

.

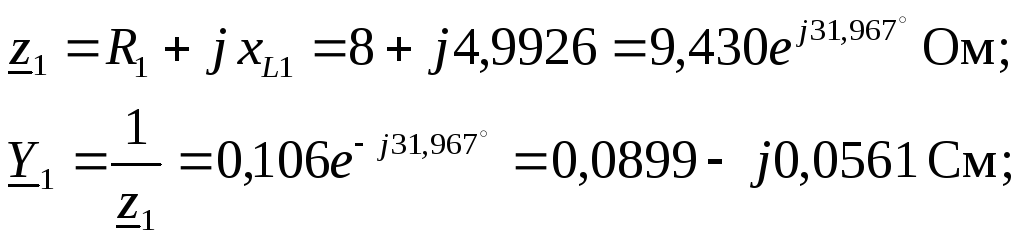
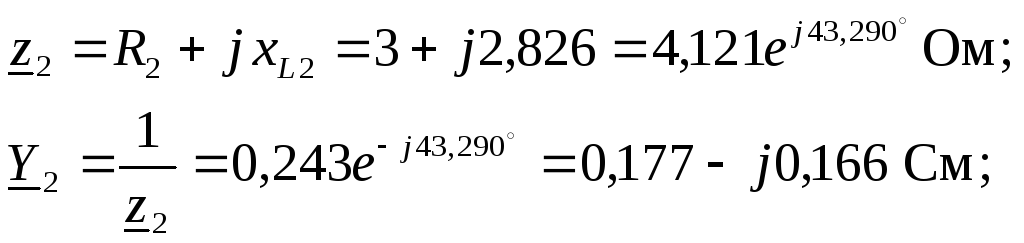
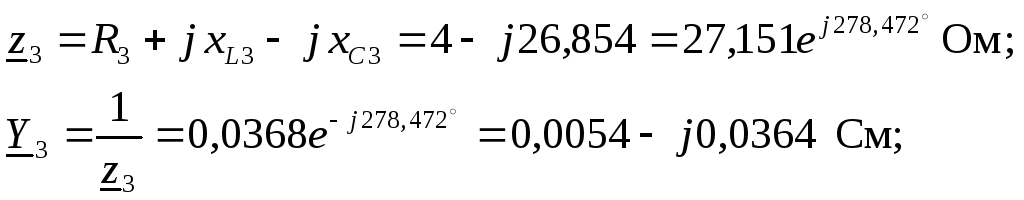
3. Рассчитываем токи в ветвях методом двух узлов. Задаем произвольно положительное направление токов в ветвях и положительное направление узлового напряжения. Используя основную формулу метода, рассчитываем узловое напряжение

.

Определяем токи в ветвях, используя обобщенный закон Ома

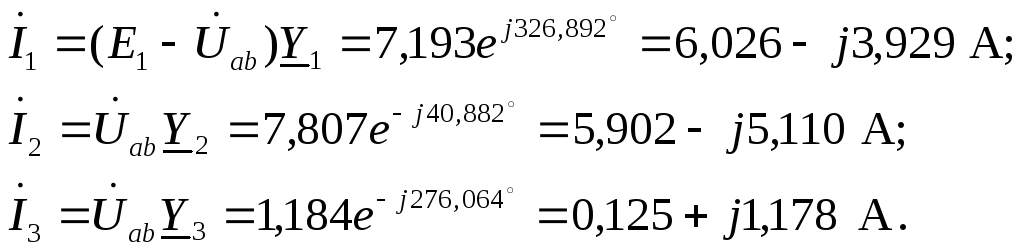
Проверяем корректность промежуточных расчетов, составив уравнение по первому закону Кирхгофа для узла а

.

Комплексная абсолютная погрешность расчета составляет

.

Определяем ее модуль

.

Рассчитываем относительную погрешность определения токов

.

Поскольку , расчет токов корректен. Первый пункт задания выполнен.

4. Составляем и проверяем баланс мощностей

Рассчитываем полную комплексную мощность, развиваемую источником, а также его активную и реактивную мощность. При этом используем закон Джоуля – Ленца в комплексной форме записи

,

.

Определяем суммарную активную и реактивную мощность на приемниках. При этом также используем закон Джоуля – Ленца

;

.

Рассчитываем суммарную полную комплексную мощность на приемниках

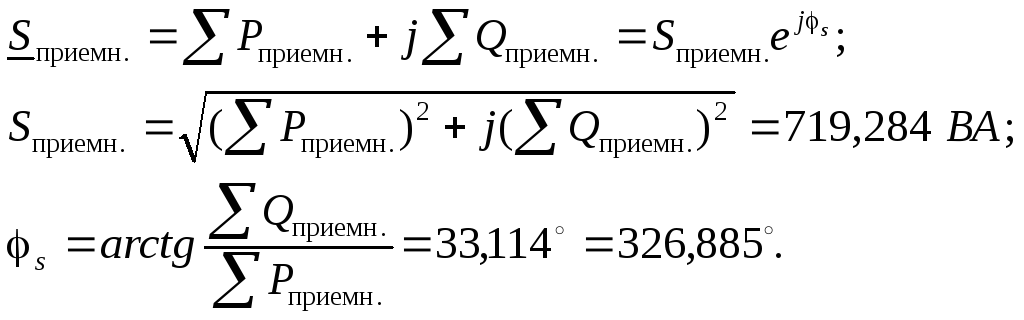
Проверяем корректность расчета, рассчитав модуль относительной погрешности определения полных мощностей

.

Расчет проведен корректно. Второй пункт задания выполнен.

5. Строим векторную диаграмму токов на комплексной плоскости, используя их действительные () и мнимые () составляющие. Задаемся масштабом по току, делим указанные составляющие токов на масштаб и откладываем получающиеся отрезки в сантиметрах вдоль осей комплексной плоскости (с учетом знаков составляющих).

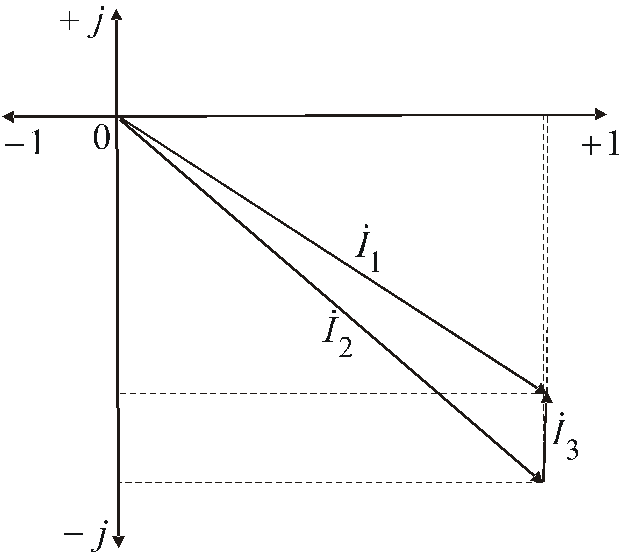
Рис. 11.

Результаты построения (рис. 11) наглядно иллюстрируют корректность проведенных расчетов. Итак, третий пункт и все задание выполнены.

При выполнении задания №2 можно также воспользоваться рекомендуемой литературой [2, 3, 4].

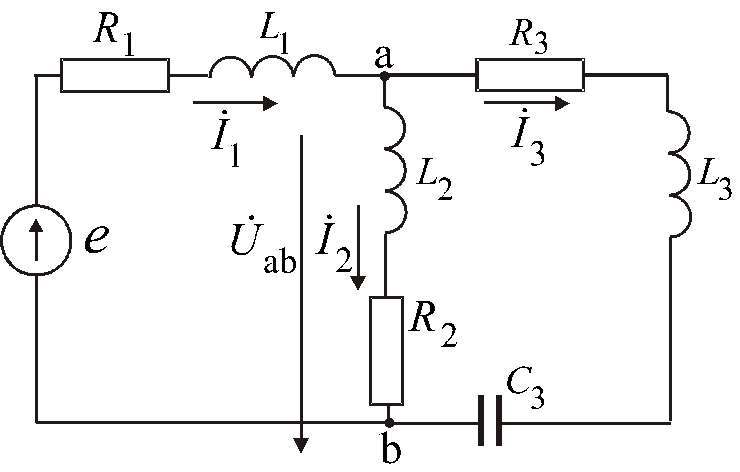
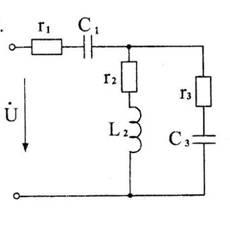
Пример 6. Для цепи, изображенной на рис. 1 требуется:

1. Определить комплексным методом действующие значения напряжений и токов на всех участках цепи.

2. Определить активные, реактивные и полные мощности каждого участка цепи и всей цепи.

3. Составить баланс активных и реактивных мощностей и оценить погрешность расчета.

4. Построить векторную диаграмму токов и напряжений.

Рис. 1

Исходные данные: U = 127 В , r1 = 15 Ом , C1 = 60 мкФ, r2 = 10 Ом , L2 = 80 мГн, r3 = 15 Ом , C3 = 90 мкФ. Частота питающего напряжения 50 Гц.