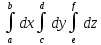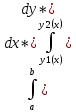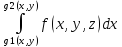matem1
.docx|
1. Первообразная. Понятие неопределенного интеграла Первообра́знойданной функции f называют такую F, производная которой равна f, то есть F′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием. К результату первообразной прибавляется С, где С любое число. Если
F —
первообразная интегрируемой функции
f,
то: Это соотношение называется формулой Ньютона — Лейбница. Благодаря
этой связи множество первообразных
данной функции f
называют неопределённым
интегралом f
и записывают в виде интеграла без
указания пределов:
|
2. Свойства и таблица неопределенных интегралов Свойства неопределенного интеграла В приведенных ниже формулах f и g - функции переменной x, F - первообразная функции f, а, k, C - постоянные величины.
Таблица интегралов
|
3.Способы инт-ия. Непосредственное инт-ие. Инт-ие подстановкой и заменой Большинство интегралов кроме непосредственного интегрирования находятся с помощью подстановки т.е. методом замены переменной. Подынтегральное выражение представляет собой дифференциал т.к. подынтегральное выражение есть произведение подынтегральной ф-ии udx. Если учесть ф-лу вычисления дифференциала dF(x)=F’(x)dx, то можно на ее основе производить поднесение под знак дифференциала (xdx=d(x^2/2)) |
4. Способы инт-ия. Инт-ие по частям Т.к.
по правилу дифференцирования
произведения имеем (u*v)’=
u’*v+u*v’,
а дифференциал d(uv)=du*v+udv,
то формула интегрирования по частя
имеет вид:
Интегрирование по частям применяется когда подынтегральная ф-ия представляет собой произведение двух ф-ий каждая из которых может быть многочленом, тригоном-ой, логориф-ой или показательной ф-ией. |
5. Способы инт-ия. Инт-ие рациональных дробей. Простейшие дроби Простейшие рациональные дроби являются правильными и бывают 4 типов: 1) Любую правильную рациональную дробь можно однозначно представить в виде суммы конкретных простейших дробей Если подынтегральная дробь неправильна, то необходимо при интегрировании в начале путем деления числителя на знаменатель выделить ее целую и дробную части |
|
6. Способы инт-ия. Инт-ие правильных и неправильных рациональных дробей Рациональные дроби могут быть правильными и неправильными. 1) Правильная – если степень числителя строго меньше знаменателя, в противном случае - неправильная. При интегрировании правильной дроби надо предствить ее в виде суммы конкретных простейших дробей 1-4. Если подынтегральная дробь неправильна, то необходимо при интегрировании в начале путем деления числителя на знаменатель выделить ее целую и дробную части |
7. Способы инт-ия. Инт-ие некоторых иррациональных выражений 1) 2)Когда
интеграл содержит
Данный интеграл сводится к табличным выделением в квадратном трехчлене полного квадрата. |
8. Способы инт-ия. Инт-ие тригонометрический ур-ий Инт-ие тригоном-ких рациональных выражений осуществляется с помощью универсальной тригоном-ой заменой tg(x/2)=t. В случае когда триг-ое рациональное выражение является четной ф-ией т.е. содержит четные степени тогда чтобы избежать высоких степеней используют замену tgx^2=t. В результате такой замены получается рациональная дробь относительно «невысоких» степеней t. Интег-ие произведения натуральных степеней производятся с помощью поднесения под знак дифференциала одного из нечетных степеней sin или cos и с использованием триг-их ф-л 1) 2)Когда обе степени четные тогда применяют формулы понижения степени
|
9. Интегральные суммы и их св-ва Основное св-во интегральных сумм m(b-a)≤Sn≤Ŝn≤M(b-a) Интегральной
суммой для ф-ии y=f(x)
неприрывной на отрезке (a;b)
является сумма f(t1)*∆x1+…+f(tn)*∆xn= *∆xi=Sn Очевидно, что интегральная сумма зависит как от способа разбиения отрезка [а, b] точкам так и от выбора точек на каждом из отрезков разбиения |
10. Опред. интеграл и теорема о его существовании T. Если y=f(x) непрерывна на отрезке [a,b], то она интегрируема на нем. Факты из Т.: 1)Опред. интеграл зависит только от вида подынтегральной ф-ии и пределов интегрирования. Такое св-во называют св-ом индифферентности(безразлич); 2)Из
определения вытекает, что a<b,
тогда при замене приделов интегрирования
местами имеем
3)Интеграл
|
|
11. Опред. интеграл и его св-ва Определенный интеграл – это интеграл у которого есть пределы интегрирования. 1) Постоянный множитель выносится из под знака интеграла; 2) Определенный интеграл суммы есть сумма определенных интегралов; 3)
Если на отрезке[a;b]
для любых x,
f(x)≤g(x),
то
4)
Если на отрезке[a;b]
f(x)
принимает наименьшее значение m
и M
- наибольшее значение, то
m(b-a)≤ 5)
Теорема о среднем. Если непрерывная
ф-ия на [a;b]
интегрируема, то всегда на этом отрезке
найдется точка
6)
Для любых чисел a,
b,
с таких что a<c<b
выполняется
|
12. Опред. интеграл и его вычисление. Формула Ньютона-Лейбница Т…Если
F(x)
является первообразной неприрывной
ф-ии f(x),
то справедлива ф-ла Ньютона- Лейбница
Док-во:
Пусть F(x)
является первообразной неприрывной
на [a,b]
ф-ии f(x).
Такая первообразная действительно
будет существовать по теореме. А т.к.
F(x)
– первообразная f(x)?
то они будут отличаться на константу
С.
Пусть x=a, тогда .
Пусть
x=b,
тогда
|
13. Опред. интеграл и методы его вычисления Пусть
имеется опред. интеграл вида
Если ф-ия f(t) непрерывна на любом [a,x], то Ф’(x)=f(x). Если
F(x)
является первообразной непрерывной
ф-ии f(x),
то справедлива ф-ла Ньютона-Лейбница
При нахождении опред. интеграла в случае необходимости замены переменной надо изменить и пределы инт-ия. |
14. Системы координат и способы задания в них ф-ий Известно
на пл-ти декартовая прямоугольная
система коорд. Определяемая
ортонормированным базисом
|
15. Приложение опред. интегралов. Вычисление площадей Исходя
из геометрического смысла опред.
интеграла имеем, что если ф-я
y=f(x)≥0Vxε[a;b]
в декартовой прямоуг. Системе координат
Если
кривая пресекает какую либо ось, то
ее находят как площади ее частей S1= Если
криволинейная трапеция ограничена
сверху и снизу кривыми дуг то:
S
криволинейного сектора:
|
|
16. Приложение оипред. интегралов. Вычисление длин дуг Пусть
в декартовой системе координат
непрерывная кривая на [a,b]
задана y=f(x),
тогда дуга AB
находится
Пусть
непрерывная кривая задана в декартовой
системе параметрически, тогда длинна
дуги находится:
Пусть
в полярной системе задана непрерывная
ф-ия r=r(φ),
|
17. Комплексные числа. Алгебраическая форма. Комплексное
число – это мнимая единица обозначаемая
буквой
Алгебраической формой комплексного числа ZεC называется его запись с помощью двух действительных чисел xεR; yεR в следующем виде: z=x+y*i, т.е. это алгебраическая форма комплексного числа. При этом x называют действительной частью комплексного числа z, а y – мнимой частью комплексного числа z. Поэтому любое действительное число будет иметь в этой форме мнимую часть =0. Т.к. всякое комплексное число определяется x и y, то его можно изобразить как точку с координатами (х;у) на комплексной пл-ти. |
18. Комплексные числа. Тригон-ая и показательная ф-лы Комплексное
число – это мнимая единица обозначаемая
буквой
Триг-ая форма комплексного числа: Пусть
дано z=x+yi
тогда его можно изобразить точкой на
комплексной пл-ти, которое будет
задаваться не только x
и y,
но и расстоянием до начала координат,
а также углом, который составляет
радиус вектор с осью абсцисс. Тогда
из полученного прямоугольного
треугольника имеем x=rcosφ,
y=rsinφ,
тогда z=x+yi=rcosφ+rsinφi=
r(cosφ+isinφ)
– триг-ая форма комплексного числа
z,
где r=│z│= Если
комплексное число в алгебраической
форме z=x+yi
имеет своим модулем r
и arg
z=φ,
то в показательной форме такое число
будет иметь следующий вид z=r* |
19. Комплексные числа и основные операции над ними Комплексное
число – это мнимая единица обозначаемая
буквой
В алгебраической форме комплексные числа записываются как z=x+yi. Комплексные числа можно складывать и отнимать т.е.: Z1+Z2=(x1+y1i) x1+x2±(y1+y2)*i=x3±y3i Умножать: Z1*Z2=(x1+y1i)*(x2+y2i)= (x1*x2)+(x1*y2i)+(y1i*x2)+ (y1i*y2i)=…=x3+y3i Делить:
Возводить в квадрат и куб (3+2i)^2=9+2*3*2i+(2i)^2= 9+12i-4=5+12i |
20. Комплексные числа. Ф-ла Муавра Комплексное
число – это мнимая единица обозначаемая
буквой
Если
комплексное число в алгебраической
форме z=x+yi
имеет своим модулем r
и arg
z=φ,
то в показательной форме такое число
будет иметь следующий вид z=r* Для нахождения степеней комплексных чисел применяют ф-лу Муавра, которая для положительных, целых чисел n в триг-ой и показательной формах имеют вид:[r(cosφ+isinφ)]^n= (cosnφ+isinφ);
|
|
21. Комплексные числа. Ф-ла корня n-ой степени Комплексное
число – это мнимая единица обозначаемая
буквой
Извлечение корней из комплексных чисел в триг-их и показательных формах производят по формуле:
|
22. Ф-ии нескольких переменных. Основные понятия Под ф-ией нескольких переменных называется такое соответствие по которому нескольких значениях независимых переменных ставятся соответствия конкретное значение зависимой переменной, то есть значения ф-ии. Задания такой ФНП можно осуществить также как и ф-ии одной переменнной разными способами: -Аналитически (в виде ф-лы)4 -Таблично; -Графически; -В текстовом виде. z=F(x;y)- ф-ла задающая ФНП. Областью определения z=F(x;y) будет множества пар чисел(множество точек) |
23. Ф-ии нескольких переменных. Непрерывность и частные производные Ф-ия
z=F(x;y)
называется непрерывной в т.
Для
нахождения частной производной
|
24. Ф-ии нескольких переменных. Локальный экстремум ФНП
z=F(x;y)
имеет экстремум в точке
Теорема:
Если ф-ия z=F(x;y)
в точке
|
25. Ф-ии нескольких переменных. Наибольшее и наименьшее значение заданной области Пусть на области D задана непрерывная ф-ия z=F(x;y). Область D является частью области определения DεD(F) и представляет собой часть координатной пл-ти xoy как множества точек с координатами (x;y) лежащих внутри D, которая ограничена некоторым контуром. Тогда наибольшее и наименьшее значения ф-ии z=F(x;y) следует искать среди точек внутри или на самом контуре L. 1)Наибольшее и наименьшее значения z=F(x;y) внутри контура L следует искать среди стационарных точек; 2)Среди критических точек или среди граничных точек в которых формула заданная L меняет свой вид; 3)После установления координат таких точек находят значения ф-ии z=F(x;y) и сравнивая их находят наибольшее и наименьшее значения
|
|
26. Ф-ии нескольких переменных. Полное приращение и полный дифференциал Линейная (относительно ∆x и ∆y) часть полного приращения функции называется полным дифференциалом и обозначается dz:
Пусть
задана функция z=f(x;y).
Если аргументу x
сообщить приращение ∆x,
а аргументу y
– приращение ∆y,
то функция z=f(x;y).
получит приращение ∆z,
которое называется полным
приращением функции
и определяется формулой: ∆z=f(x+∆x,
y+∆y)-f(x,y).
Функция
z=f(x;y).,
полное приращение ∆z
которой в данной точке может быть
представлено в виде суммы двух слагаемых
(выражения, линейного относительно
∆x
и ∆y,
и величины бесконечно малой высшего
порядка относительно):
|
27. ДУ-1 основные понятия Диф-ми называются ур-ия, в которых искомыми являются ф-ии одной или нескольких переменных, причем в эти ур-ия входят как сами искомые ф-ии, так и их произв-ые Порядок старшей из произв-ых или старшего из диф-ла искомой ф-ии называется порядком диф-ого ур-ия. Если искомая ф-ия зависит от одного аргумента, то диф-ное ур-ие называют обыкновенным. Если искомая ф-ия зависит от нескольких переменных и ур-ие содержит частные производные, то оно называется ур-ем в частных производных. Диф-ое ур-ие n-ого порядка в общем случае имеет вид:F(x, yn, yn-1, … y’, y)=0 Решением диф-ого ур-ия n-ого порядка называется ф-ия f(x), имеющая на некотором интервале (a,b) производные до порядка n включительно, которая будучи представлена в ур-ие обращает его в тождество F(x,f(x), f’(x), … fn(x))=0 График решения диф-ого ур-ия называется интегральной кривой этого уравнения. Процесс нахождения решения диф-ого ур-ия называется интегрированием уравнения.
|
28. ДУ-1 с разделенными и разделяющимися переменными ДУ-1 могут иметь следующий вид φ(x)dx+ψ(y)dy=0, то оно называется с разделенными переменными. И в случае непрерывности ф-ии φ(x) и ψ(y) такое равенство можно проинтегрировать с учетом св-ва интегралов. Если ДУ-1 представлена в виде φ1(x)+ψ1(y)dx+ φ2(x)φ2(y)dy=0 то оно называется с разделяющимися переменными т.к. простые алгебраи-ие операции позволяют преобразовать его к ДУ с разделенными переменными. Такое разделение следует провести перед его интегрированием. |
29. ОДУ-1 Уравнение
вида y’=f( ОДУ-1
приводится к ДУ с разделяющимися
переменными с помощью замены
y’=(ux)’=u’x+u |
30. ЛДУ y’+p(x)*y=f(x) – называется линейным ДУ первого порядка. Если f(x)≡0, то это ур-ие однородное, в противном случае неоднородное. Для решения уравнения используются подстановка y=u(x)*v(x). Тогда, по правилу дифф-ия произведения y’=(uv)’=u’v+uv’ подставляя в ур-ие получим y’+p(x)*y=f(x) u’v+uv’+p(x)*uv=f(x) Группируем второе и треть слагаемое ф-и и выносим за скобки u’v+u*(v’+p(x)*v)=f(x) Далее скобку приравниваем к 0 v’+p(x)*v=0 Тогда u’v=f(x)
|
|
31. ДУ в полных дифференциалах Уравнение З(x;y)*dx+Q(x;y)*dy=0 – ур-ие в полных дифференциалах если его целая часть представляет собой полный диф-ал некоторой ф-ии u(x;y). Тогда это ур-ие можно переписать в виде: du(x;y)=0, а его общий интеграл u(x;y)=c. Для
того чтобы выражение p(x;y)dx+Q(x;y)dy
являлось полным диф-лом надо чтобы
во всех точках выполнялось условие
|
32. ДУ-1 Бернулли y’+p(x)y=f(x) Разделим
обе части на
Z(x)= Z’(x)=1-α*
|
33. ДУ высшего порядка, позволяющие его понизить Такие ДУ позволяют с помощью определенных методов свести их решение к ДУ-1 Например: 1) 2)F(y”,y’,x)=0 – тогда заменой y’=u(x), а значит y”=u’(x). Данное ДУ приводится к ДУ-1, которая имеет вид: Ф(u’,u,x)=0 3)F(y”;y’;y)=0 – такое ДУ понижает порядок до первого заменой y’=u; y”=u*y’=u’*u |
34. ЛОДУ ДУ вида ay”+by’+cy=0, где а≠0, а,в,с=const – ЛОДУ-11 Решение
ЛОДУ-11 основано на нахождении корней
его характеристического ур-ия. Хар-им
ур-ем ЛОДУ-11 называется квадратное
уравнение которое получается из
ЛОДУ-11 заменой производных 1 и 11 порядка
на первую и вторую степень λ. Для
нахождения общего решения ЛОДУ-11
находят фундаментальную систему его
решений
Случаи решений: 1)Если
Д>0 – два различных действительных
корня, тогда
2)Если
Д=0, то ЛОДУ имеет два одинаковых
действительных корня 3)Если Д<0, то два комплексных корня. λ1=a=bi λ2=a-bi
|
35. ЛНОДУ с постоянными коэф. И спец. Правой частью Уравнение
вила аy”+by’+cy=f(x)
называется ЛНОДУ-11 с постоянными
коэффициентами, а если ф-ия f(x)
имеет вид 1)
f(x)= Общим
решением ЛНОДУ-11 является такая ф-ия
у которая представима в виде суммы
двух ф-ий y= ỹ=Pn(x)* Если правая часть ЛНОДУ-11 представима в виде ф-ии 2) f(x)=( То частное решение ỹ также имеет определенный вид который определяется по виду 2. После того как по виду f(x) определен общий вид ỹ, его вместе со своими 1-й и 2-й производными подставляют в исходное ЛНОДУ и из полученного равенства получают неизвестные коэффициенты. |
|
36. Двойной интеграл и его вычисление Для упрощения вычисления двойного интеграла часто применяют метод подстановки, т. е. вводят новые переменные под знаком двойного интеграла. Вычисление двойного интеграла анологично вычислению определенного интеграла, а значит двойной интеграл обладает теми же св-ами, что и определенный. Вычисление ∫∫ сводится к повторному интегрированию для чего необходимо: 1)Определить по каким переменным будет находиться внутренний и внешний интеграл. 2)Для чего определяют правильность области инт-ия D вдоль какой то оси. Тогда если D правильная вдоль оси OX, То внутренний интеграл по Х, а если OY, то y. 3) затем расставить пределы инт-ия по правилу: внешнего по линиям, внутреннего по точкам. |
37. Приложение двойных интегралов С помощью ∫∫ можно вычислить площадь плоской фигуры по ф-ле S=∫∫dxdy, где S – площадь фигуры Д. 1)V=∫∫f(x,y)ds 1’) V=∫∫f(x,y)dxdy 2)
2’) |
38. Тройной интеграл и его вычисление Вычисление ∫∫∫ для прямоугольной области: Пусть область V представляет собой параллелепипед{a≤x≤b; c≤y≤d; e≤z≤f} ∫∫∫f(x,y,z)dxdydz=
Вычисление ∫∫∫ в криволинейной области ∫∫∫f(x,y,z)dxdydz=
|
39. Приложение тройного интеграла Тройной интеграл обладает теми же св-вами его вычисления , что и двойной, и определенный. Он имеет вид: ∫∫∫f(x,y,z)dxdydz 1)∫∫∫dxdydz=v, где v – объем области V. 2)∫∫∫[αf(x,y,z)+βg(x,y,z)]dxdydz= α∫∫∫f(x,y,z)dxdydz+ β∫∫∫g(x,y,z)dxdydz Теорема о среднем: Пусть f(x,y,z)непрерывна в ограниченной области V тогда существует точка pεv такая, что ∫∫∫f(x,y,z)dxdydz=f(P)*v |
|

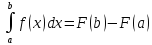
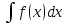 .
Каждая последующая первообразная
отличается на С.
.
Каждая последующая первообразная
отличается на С.
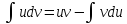 Эта ф-ла используется когда новый
интеграл получается проще исходного.
Также используется правило: за множитель
u
надо выбрать такой из множителей,
который при диффер-ии наиболее
упрощается по сравнению с другими.
Эта ф-ла используется когда новый
интеграл получается проще исходного.
Также используется правило: за множитель
u
надо выбрать такой из множителей,
который при диффер-ии наиболее
упрощается по сравнению с другими.
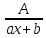 ;
2)
;
2)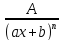 ;
3)
;
3)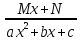 ;
4)
;
4)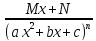
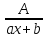 ;
2)
;
2)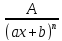 ;
3)
;
3)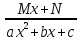 ;
4)
;
4)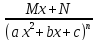
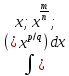 ,
где m,
n,
p,
q
– натуральные числа. Такие интегралы
сводятся к интегралам от рациональных
дробей путем подстановки (x=u^t,
dx=tu^(t-1)du.
,
где m,
n,
p,
q
– натуральные числа. Такие интегралы
сводятся к интегралам от рациональных
дробей путем подстановки (x=u^t,
dx=tu^(t-1)du.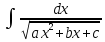
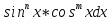
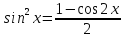
 =-
=-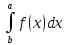 ;
;
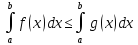 ;
;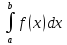 ≤M(b-a);
≤M(b-a);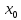
 ;
;
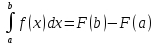
 .
Данное равенство справедливо для
любого x,
главное чтобы на [a,x]
ф-ия f(t)
была непрерывной.
.
Данное равенство справедливо для
любого x,
главное чтобы на [a,x]
ф-ия f(t)
была непрерывной.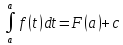 ,
а по факту
,
а по факту
 ,
тогда с=-F(a)
,
тогда с=-F(a)
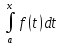 у которого нижний предел зафиксирован,
а верхний переменный, а т.к. опред.
интеграл зависит от пределов инт-ия
и не зависит от переменной t,
то этот опред. интеграл будет принимать
разные значения в зависимости от
значения верхнего предела x.
у которого нижний предел зафиксирован,
а верхний переменный, а т.к. опред.
интеграл зависит от пределов инт-ия
и не зависит от переменной t,
то этот опред. интеграл будет принимать
разные значения в зависимости от
значения верхнего предела x.
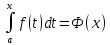
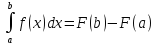
 и
и
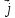 которые определяют ось абсцисс и
ординат с началом координат в т. О. В
которой всякая точка определяется
однозначно двумя координатами (x,y),
который являются проекциями на
соответ-ие координатные оси. А т.к.
всякая фигура представляет собой
множество точек поэтому любая линия
может быть записана в виде уравнения
связывающего между собой x
и y.
Существуют такие кривые, которые
задать одним ур-ем невозможно или
очень сложно. Поэтому такие кривые
задают параметрически:
которые определяют ось абсцисс и
ординат с началом координат в т. О. В
которой всякая точка определяется
однозначно двумя координатами (x,y),
который являются проекциями на
соответ-ие координатные оси. А т.к.
всякая фигура представляет собой
множество точек поэтому любая линия
может быть записана в виде уравнения
связывающего между собой x
и y.
Существуют такие кривые, которые
задать одним ур-ем невозможно или
очень сложно. Поэтому такие кривые
задают параметрически:
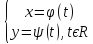
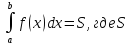 площадь
кривленной трапеции ограниченной
снизу, осью абсцисс с верху, а с лева
и с права параллельными прямыми.
площадь
кривленной трапеции ограниченной
снизу, осью абсцисс с верху, а с лева
и с права параллельными прямыми.
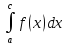 ; S2=
; S2=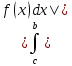
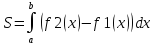
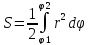
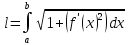
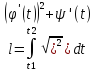
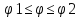 тогда дуга АВ находится как:
тогда дуга АВ находится как:
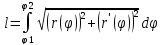
 ,
,

 ,
,
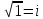
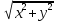 ,
φ=arg
z.
,
φ=arg
z.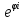
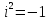 ,
,
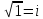
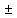 (x2+y2i)=
(x2+y2i)=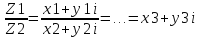
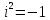 ,
,
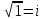
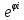
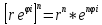
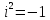 ,
,
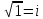
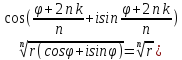

 (
( ;
; )
из D(z)
если придел LimF(x;y)=F(
)
из D(z)
если придел LimF(x;y)=F(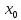 ;
;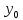 ).
Если в любой точке некоторой области
ф-ия z=F(y)
непрерывна, то вся область называется
областью непрерывности ф-ии. Точка
z=F(x;y)
называется точкой разрыва
).
Если в любой точке некоторой области
ф-ия z=F(y)
непрерывна, то вся область называется
областью непрерывности ф-ии. Точка
z=F(x;y)
называется точкой разрыва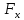 ’=
’= надо найти производную рассматривая
y
как константу, а для нахождения
надо найти производную рассматривая
y
как константу, а для нахождения
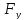 ’=
’=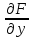 рассматривая x
– const.
рассматривая x
– const.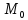 (
(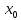 ;
;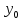 )
в виде локального max
(min)
если для любых точек из радиус
окрестности r(
)
в виде локального max
(min)
если для любых точек из радиус
окрестности r(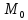 )
при сколь угодно малом радиусе r
выполняется неравенство F(
)
при сколь угодно малом радиусе r
выполняется неравенство F(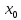 ;
;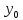 )≥F(x;y)
(F(
)≥F(x;y)
(F(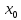 ;
;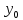 )≤F(x;y)).
При этом наибольший из всех локальных
max
(наименьших min)
называется глобальным max
(min)
ФНП.
)≤F(x;y)).
При этом наибольший из всех локальных
max
(наименьших min)
называется глобальным max
(min)
ФНП.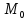 (
(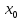 ;
;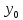 )єD(F)
имеет локальный экстремум, то эта
точка является стационарной точкой
ф-ии. Локальный экстремум надо искать
только в стационарных точках
)єD(F)
имеет локальный экстремум, то эта
точка является стационарной точкой
ф-ии. Локальный экстремум надо искать
только в стационарных точках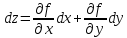 где
dx
и
dy
–
дифференциалы независимых переменных,
которые, по определению, равны
соответствующим приращениям ∆x
и
∆y.
где
dx
и
dy
–
дифференциалы независимых переменных,
которые, по определению, равны
соответствующим приращениям ∆x
и
∆y.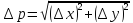
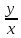 )–ОДУ-1
)–ОДУ-1 =u
отсюда y=ux
=u
отсюда y=ux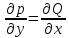
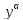 -
уравнение Бернулли
-
уравнение Бернулли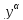
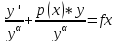

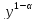
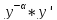
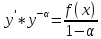
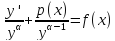
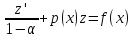
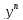 =f(x)
– такие ДУ интегрируются столько раз,
каков порядок этого ДУ;
=f(x)
– такие ДУ интегрируются столько раз,
каков порядок этого ДУ;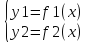 т.е. общее решение ЛОДУ имеет вид
y=c1y1+c2y2.
т.е. общее решение ЛОДУ имеет вид
y=c1y1+c2y2.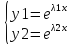
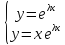
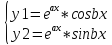
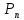 (x)*
(x)*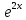 – со спец. правой частью.
– со спец. правой частью.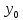 +ỹ
+ỹ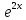 *
*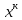 ,
где к – число совпадений.
,
где к – число совпадений.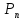 (x)cosβx+
(x)cosβx+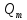 (x)sinβx)
(x)sinβx)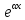
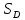 =∫∫ds
=∫∫ds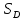 =∫∫dxdy
=∫∫dxdy