СибГАУ_Типовой расчет ТВиМС_Вариант 12

1.Имеется m радиолокационных станций, каждая из которых за один цикл обзора обнаруживает объект с вероятностью p (независимо от других циклов и от других станций). За определенное время каждая станция успевает сделать n циклов. Найти вероятность того, что объект будет обнаружен каждой из станций.

Решение.

Объект будет обнаружен одной станцией за n циклов с вероятностью: рn. Соответственно, объект будет обнаружен m станциями за n циклов с

вероятностью: Р(А) = m рn.

Ответ: m рn.

2. Имеются две урны: в первой находится 4 красных и 3 синих шара, во второй – 5 красных и 8 синих шара. Из первой урны во вторую случайным образом перекладывают два шара. После этого из второй урны берут четыре шара. Найти вероятность того, что синих и красных шаров будет одинаковое число.

Решение. Обозначим события:

А1 — из первой урны во вторую переложили 2 красных шара; А2 — из первой урны во вторую переложили 2 синих шара;

А3 — из первой урны во вторую переложили 1 красный и 1 синий шары. В — из второй урны вынули 2 красных и 2 синих шара.

После перекладывания во второй урне становится: 5 + 8 + 2 = 15 шаров. Вероятности событий:

Найдем вероятность того, что синих и красных шаров будет одинаковое число:

Р В 0,286 0,431 0,143 0,330 0,5710,396 0,3962

Ответ: 0,3962.

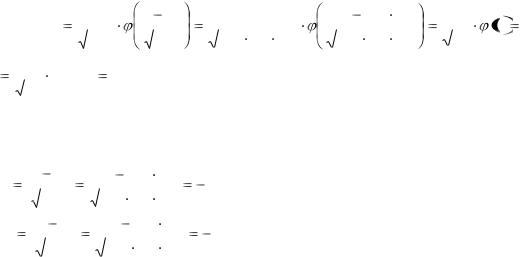
3. Монету бросают 300 раз. Найти вероятность того, что герб появится: а) ровно 150 раз; б) больше 135, но меньше 145 раз.

Решение.

Вероятность того, что событие наступит равна: р = 0,5.

Вероятность того, что событие не наступит равна: q = 1 – р = 1 – 0,5 = 0,5.

а) Определим вероятность, что в 300 испытаниях герб появится: ровно m=150 по локальной теореме Лапласа:

б) Определим вероятность, что герб выпадет больше 135, но меньше 145 раз по интегральной теореме Лапласа:

Р300(135, 145) = Ф(x'') – Ф(x')

Р300(135, 145) = Ф(–0,58) – Ф(–1,73) = –Ф(0,58) + Ф(1,73) = –0,2190 + 0,4582 = 0,2392.