u-lectures сопромат

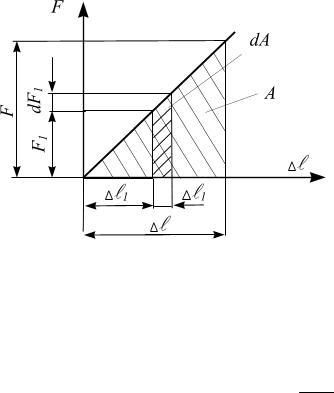
41

Рис. 2.12

Подставляя сюда вместо внешней силы F равную ей внутреннюю силу N и удлинение по формуле (2.24), получим

U = N 2l. 2EA

(2.29)

Если поперечное сечение или продольная сила меняются по длине стержня, то потенциальную энергию определяют суммированием по участкам dz:

Чтобы судить об энергоемкости материала, вводят понятие удельной потен-

циальной энергии:

где V = Al – объем стержня. С учетом формул (2.5) и (2.3) имеем:

В системе СИ за единицу работы и энергии принят джоуль [Дж], тогда удельная энергия деформации выражается в Дж/м3.

42

Из формулы (2.31) следует, что при одном и том же напряжении запас энергии тем больше, чем меньше E . Поэтому, например, резина является одним из самых энергоемких материалов, и ее используют в амортизирующих устройствах для смягчения динамических воздействий.

Статически неопределимые задачи при растяжении (сжатии) и методика раскрытия неопределимости.

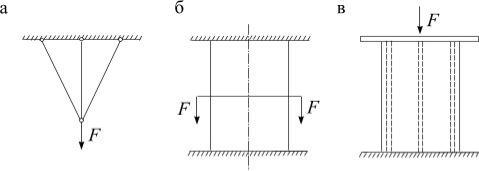
В практике статически неопределимые задачи находят широкое применение. Это мосты, каркасы жилых зданий и промышленных сооружений, валы крупных турбогенераторов и др. Схемы некоторых статически неопределимых конструкций изображены на рис. 2.13: а – стержневая подвеска; б – стержень, жестко закрепленный обоими концами; в – железобетонная колонна, состоящая из бетона с включенной в него арматурой (стальными стержнями).

Рис.2.13

В статически неопределимых системах нельзя определить реакции связей и усилия в элементах, пользуясь только уравнениями статического равновесия.

Для решения данной задачи необходимо применение дополнительных уравнений, которые можно записать, рассмотрев деформированное состояние системы. Дополнительные уравнения представляют собой уравнения совме-

стности деформаций (или кратко называются деформационными).

Расчет статически неопределимой системы рассмотрим на примере статически неопределимого ступенчатого бруса.

Пример.

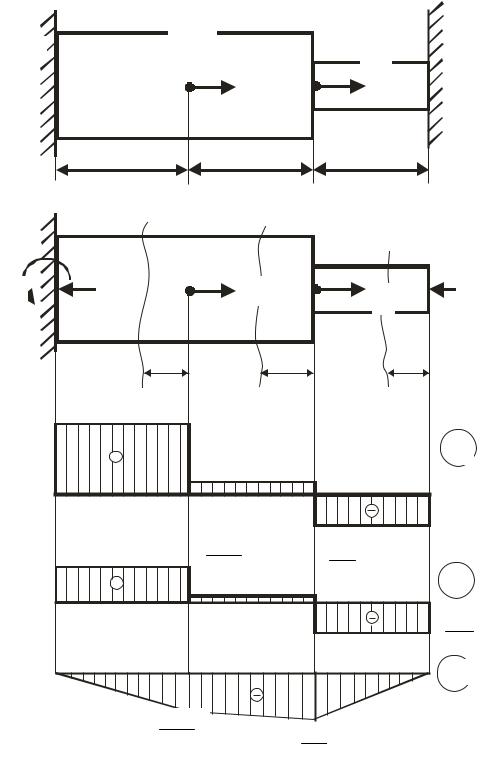
Для бруса с жёстко заделанными концами и нагруженного, как показано на схеме (рис. 2.14, а), требуется: раскрыть статическую неопределимость и построить эпюры продольных сил N, нормальных напряжений σ и перемещений δ.

Известно, что Р1 = Р, Р2 = 2Р, значение силы

Решение

Задача один раз статически неопределима, так как для системы сил, дейст-

43

вующих вдоль оси бруса, можно составить только одно уравнение равновесия

мент в заделке MA и реакция вдоль вертикальной оси равны нулю. Составим дополнительное уравнение – уравнение перемещений или деформационное. Для этого отбросим правую опору, заменим её воздействие на брус усилием RB и запишем выражение для перемещения сечения В. Исполь-

зуя принцип независимости действия сил, это перемещение выразим как сум-

в отдельности. Так как сечение В жестко заделано, то его перемещение равно нулю, и поэтому уравнение перемещений получим в виде

45

Записав деформации по закону Гука, имеем

отсюда, после сокращения на а и EA, получим RB =17,5кН.

В соответствии с расчётной схемой (рис. 2.14) аналитические зависимости продольных сил N, напряжений σ и перемещений δ будут следующими:

На основании полученных данных строим эпюры сил N, напряжений σ и перемещений δ (рис. 2.14, в, г, д).

Построение эпюры перемещений может служить контролем правильности решения задачи: перемещение на Ι участке при z = 0 и перемещении на ΙΙΙ

участке при z = a должны равняться нулю, так как эти два сечения соответствуют жёсткому закреплению бруса, перемещения которых невозможны. Пример решения статически неопределимых стержневых систем будет рассмотрен в теме 2.2, методика расчета статически неопределим систем наиболее подробно рассматривается в разделе 9.

46

Общий вид эпюр продольных сил и перемещений

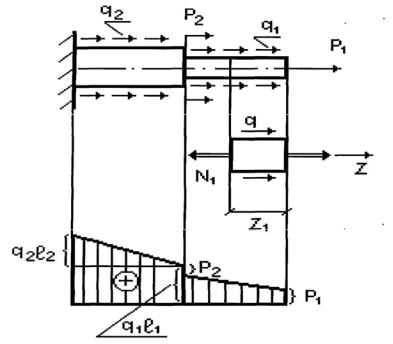
Продольная нагрузка в общем виде. Растяжение и сжатие бруса возникает при действии сосредоточенных сил и распределённой нагрузки, направленных вдоль его оси. Зная это, введём понятие унифицированная схема ступенчатого бруса при растяжении и сжатии: пусть в начале каждого грузового участка приложена сосредоточенная сила Рi, и по всему участку действует распределённая нагрузка интенсивности qi., причём за положительное считаем растягивающее направление нагрузки. Например, на рис. 2.15 изображёна схема унифицированного 2-х ступенчатого бруса.

Рис.2.15. Унифицированная схема 2-х ступенчатого бруса

При выполнении реального расчёта внешнюю нагрузку задаем числами со знаком, как показано в нижеследующем примере.

Формулы для вычисления продольной силы, общий вид и законо-

мерности эпюр. Значения продольных сил N вычисляем методом сечений, выполняя последовательно правило РОЗУ (Разрезать, Отбросить, Заменить, Уравновесить). Вычислим продольные силы в изображённом брусе с двумя грузовыми участками (рис. 2.15). В текущем сечении 1-го участка поставим силу N1 от сечения, тогда она растягивает отсечённый кусок. Такое направление продольной силы считаем положительным. Составим уравнение равновесия при растяжении и сжатии Σ пр z =0:

47

−N1 +q1z1 + P1 = 0,отсюда N1 = q1z1 + P1.

Вычислим значения силы в начале участка (при z = 0) и в конце участка (при z = l1). Получим:

N1(0) = P1, N1(l1 ) = q1l1 + P1.

Рассуждая аналогично для 2-го участка, получим в текущем сечении, удалённом от его начала на расстоянии z2,

N2 = N1(l1 ) + P2 +q2 z2 .

В начале участка (при z2 = 0) и в конце (при z2 = l2) имеем

N2 (0) = N1(l1 ) + P2 , N2 (l2 ) = N1(l1 ) + P2 +q2l2 .

Эти значения позволяют построить график изменения N вдоль оси (эпюру N) в общем виде. Она изображена на рис. 2.15 и выглядит нарастающей от свободного края по линейному закону. По ней хорошо прослеживать особенности эпюры продольной силы. А подставляя цифровые значения нагрузок реального бруса, можно получить для него эпюру N.

Для компактного представления изложенной методики вычисления продольной силы можно изобразить только один грузовой участок бруса (рис. 2.16), это любой участок бруса, который представляем по унифицированной схеме. Тогда запишем для продольной силы формулу

где NN i − значение продольной силы в начале i-го участка.

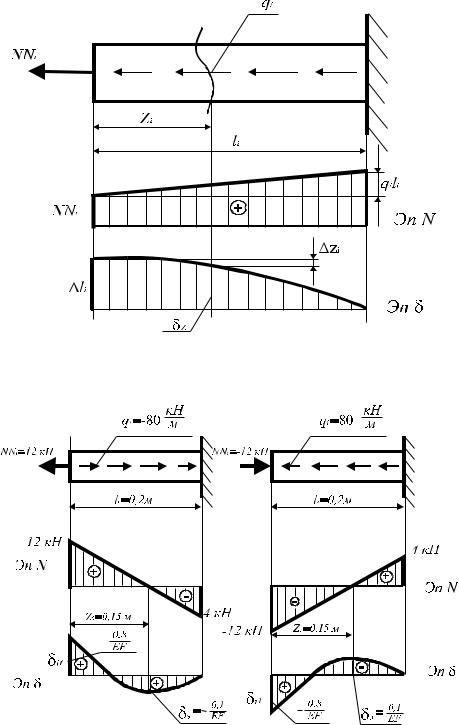
Рассмотрим пример вычисления продольной силы (рис. 2.17). Здесь для левого бруса P=12 кН, q= -80 кН/м, поэтому по (2.34) получаем

N =12 +(−80) z , при z = 0 N =12 кН, при z = 0,2м N = −4кН.

48

Рис.2.16 Унифицированная схема грузового участка ступенчатого бруса

Рис. 2.17 Пример эпюр продольных сил и перемещений

Как видим, используя унифицированное представление бруса, удобно вычислять продольные силы, прослеживать особенности эпюры и выполнять её проверку.

Формулы для вычисления перемещений поперечных сечений, общий вид и закономерности эпюр. Составим выражение для продольных смещений

49

поперечных сечений. Для перемещений необходимо знать абсолютные деформации участков бруса li,

Реальное перемещение δ1 свободного всего бруса является суммой деформаций всех участков (рис. 2.15):

где деформации участков бруса li запишем, подставляя Ni по (2.34):

Поясним вычисление перемещений на примере (см. рис. 2.17). Перемещение свободного края бруса равно деформации всего бруса, которую найдём по

(2.35),

Откладывая полученные значения, изобразим на рис. 2.17 для рассматриваемого бруса эпюру перемещений δ.

Используя (2.34) и (2.35) для унифицированной схемы бруса, можно изобразить общий вид эпюры перемещений δ (рис. 2.16), она будет нарастающей от

50

заделки по кривой 2-го порядка.

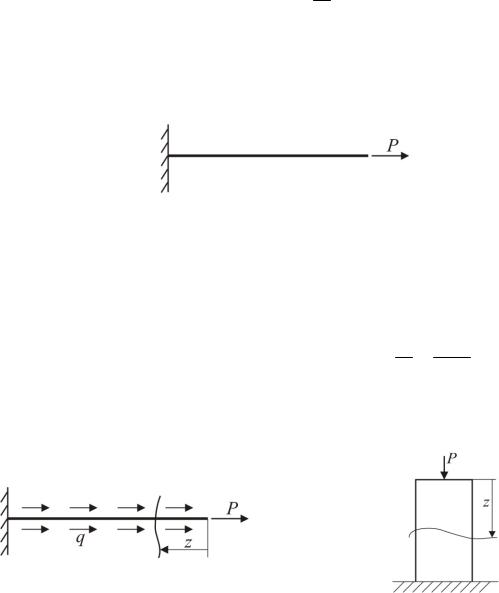
Стержень (брус) равного сопротивления

Введём понятие брус равного сопротивления – это брус, в котором во всех сечениях напряжения одинаковы, т. е. σ = NA = const по длине бруса.

Рис. 2.18

В других случаях, когда кроме сосредоточенной силы приложена распределенная нагрузка (рис. 2.19) или рассматривается массивный стержень (рис. 2.20), в котором необходимо учитывать собственный вес, продольная

сила будет переменна N = f (z) и напряжение σ = NA = f A(z) ≠ const . С эко-

номической точки зрения брус равного сопротивления выгоднее. Тогда необходимо найти усилия, при котором σ = const .

Рис. 2.19 Рис. 2.20

1 случай. Брус нагружен силой P и распределенной нагрузкой q = const (рис. 2.19).

Здесь продольная сила N = P + qz . Напряжение стремимся сделать одинаковым, тогда