u-lectures сопромат
.pdf
91
J x = ∫y2dF = Fix2 , |
(3.26) |
F |
|
где ix – радиус инерции относительно оси x . Как следует из формулы (3.26), радиус инерции относительно осей x и y соответственно будут равны
ix =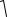 
JFx и iy = 
JFy .
Главным центральным осям инерции соответствуют главные радиусы инерции
iu =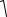 
JFu и iv = 
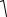JFv .
Построим на главных центральных осях инерции плоской фигуры эллипс с полуосями, равными главным радиусам инерции, откладывая при этом вдоль оси u отрезки, равные iv , а вдоль оси v – iu (рис. 3.12).
Рис. 3.12
Такой эллипс, называется эллипсом инерции, где радиус инерции относительно любой центральной оси x определяется как перпендикуляр OA , опущенный из центра эллипса O на касательную к нему, параллельную оси x .
92
Для получения точки касания достаточно провести параллельно данной оси x любую хорду. Точка пересечения эллипса с линией, соединяющей центр O и середину хорды, является точкой касания. Измерив отрезок OA = ix , находим
момент инерции по формуле (3.26).
Моменты инерции относительно параллельных осей
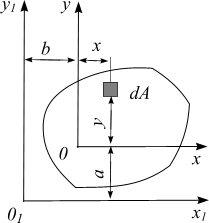
Пусть известны моменты инерции Jx , J y , Jxy для фигуры площадью А (рис.
3.13) относительно осей х и у (исходные оси). Требуется определить моменты инерции относительно новых осей х1 и у1 параллельных исходным.
Рис.3.13
Координаты площадки dA в новой системе координат:
y1 = y + a, x1 = x + в,
Где а и b – расстояния между исходными и новыми осями.
Пользуясь общими выражениями моментов инерции (3.6) и (3.9), находим
J x1 = ∫ y1 |
2 dA = ∫( y + a)2 dA = ∫ y 2 dA + 2a∫ ydA + a 2 ∫dA . |
|
|
|||
A |
A |
A |
A |
A |
|
|
Аналогично для момента инерции |
J y1 . Зависимость для центробежного мо- |
|||||
мента относительно осей x1 и y1 примет вид: |
|
|
|
|||
J x1 y1 |
= ∫ x1 y1dA = ∫(x + b)( y + a)dA = ∫ xydA + a∫ xdA + b∫ ydA + ab∫dA. |
|||||
|
A |
A |
A |
A |
A |
A |
Тогда с учетом (3.1), (3.2), (3.6) и (3.9) получим формулы моментов инерции
93
относительно параллельных осей:
|
J x = J x + 2aSx + a2 A, |
|
|
|
1 |
|
|
|
J y |
= J y + 2bS y + b2 A, |
(3.27) |
|
1 |
|
|
|
J x y |
= J xy + bSx + aS y + abA. |
|
|
1 |
1 |
|
Напомним, что |
в формулах (3.27) геометрические |
характеристики |
|
Sx , Sy , Jx , J y и Jxy |
известны и определены относительно исходных осей х, у. |
||
Если эти оси центральные, то Sx = Sy = 0 , и формулы (3.27) упрощаются:
J x |
= J x + a2 A, |
|
1 |
|
|
J y |
= J y + b2 A, |
(3.28) |
1 |
|
|
J x y |
= J xy + abA. |
|
1 |
1 |
|
Формулы (3.28) называют формулами перехода от центральных осей к осям, параллельным им или коротко формулами «параллельного переноса». Из этих формул следуют следующие определения:
•Момент инерции относительно любой оси равен моменту инерции относительно центральной оси, параллельной данной, плюс произведение площади фигуры на квадрат расстояния между этими осями.
•Центробежный момент инерции относительно произвольных осей, параллельных центральным, равен центробежному моменту относительно центральных осей плюс произведение площади сечения на расстояния между осями.
Отметим, что при вычислении моментов инерции по формулам (3.28) расстояния a и b cледует брать с учетом знака в системе координат x1 и y1,
Из формул (3.28) следует: из семейства параллельных осей минимальный момент инерции будет относительно центральной оси. Формулы 3.28 часто применяют для вычисления моментов инерции сложных фигур.
Зависимости между моментами инерции при повороте осей
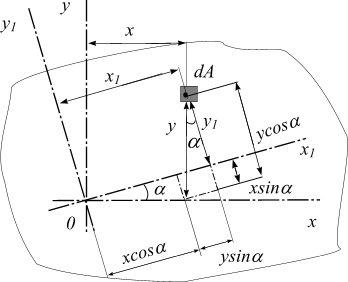
Пусть известны моменты инерции Jx , J y , Jxy произвольного сечения относительно осей x и y (рис. 3.14).
94
Рис. 3.14
Повернем оси x и y на угол α против часовой стрелки по отношению к исходным осям. Найдем моменты инерции относительно повернутых осей x1 и y1. Координаты элементарной площадки dA в новых осях:
|
|
|
x1 = x cos α+ y sin α, |
|
|
|
|
y1 = y cos α− x sin α. |
|
Найдем момент инерции относительно оси x1: |
|
|||
J x1 = ∫ y1 |
2 dA = ∫( y cos α − x sin α)2 dA = ∫ y 2 cos2 αdA − |
|
||
A |
|
A |
A |
|
− ∫2xy sin αcos αdA + ∫ x2 sin 2 αdA. |
|
|||
A |
|
|
A |
|
Аналогично для J y |
и с учетом формул (3.6) и (3.9) окончательно получим: |
|||
1 |
|
|
|
|
Jx |
|
= Jx cos2 α + J y sin2 α − Jxy sin 2α |
|
|
1 |
|
|
|
|
|
|
|
|
(3.29) |
J y |
|
= Jx sin2 α + J y cos2 α + Jxy sin 2α |
|
|
1 |
|
|
|
|
Складывая почленно формулы (3.29), определяем: |
|
|||
|
|
J x |
+ J y = J x + J y = const . |
(3.30) |
|
|
1 |
1 |
|
Cумма осевых моментов инерции относительно любой пары взаимно перпен-
95
дикулярных осей, проходящих через одно начало координат, есть величина постоянная.
Для центробежного момента относительно осей x1 и y1:
J x1 y1 = ∫ x1 y1 dA = ∫(x cos α + y sin α)( y cos α − x sin α)dA =
A A
= sin αcos α(∫ y 2 dA − ∫ x2 dA) + (cos2 α − sin 2 α)∫ xydA
A A A
или после преобразований:
J x y |
= |
J x − |
J y |
sin 2α + J xy cos 2α. |
(3.31) |
|
2 |
|
|||||
1 |
1 |
|
|
|
|
|
|
|
|
|
|
||
По формулам (3.29), (3.31) находят моменты инерции при повороте осей на угол α . Практический интерес представляет поворот осей вокруг центра тяжести.
Главные оси и главные моменты инерции
Из вышеприведенных формул следует, что при повороте осей моменты инер-
ции изменяются, но сумма осевых моментов остается постоянной.
Следовательно, если относительно одной оси значение момента инерции будет наибольшим, то относительно другой – наименьшим. В этом случае центробежный момент относительно осей оказывается равным нулю.
Главными центральными осями называются оси, проходящие через центр тяжести сечения, относительно которых центробежный момент инерции равен нулю, а осевые моменты инерции относительно данных осей обладают свойствами экстремальности и называются главными центральными моментами инерции. Относительно одной главной оси момент инерции имеет наимень-
шее значение – J min , относительно другой – наибольшее Jmax .
Будем обозначать главные оси буквами u и v. Докажем приведенное утверждение. Пусть оси x и y – центральные оси несимметричного сечения (рис. 3.15).
Определим положение главных осей путем поворота центральных осей на угол α0 , при котором центробежный момент становится равным нулю.
Jx1 y1 = Juv = 0 .
96
Рис.3.15
Тогда по формуле (3.31) |
|
|
|
|
|
|
|
J x y = |
J x − J y |
sin 2αo |
+ J xy cos 2αo = 0. |
|
|||
|
|
||||||
2 |
|
||||||
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
Откуда |
|
|
|
2J xy |
|
|
|
|
|
tg2αo = − |
. |
(3.32) |
|||
|
|
|
|
||||
|
|
J x |
− J y |
||||
|
|
|
|
|
|
||
Формула (3.32) определяет положение главных осей, где α0 – угол, на кото-
рый нужно повернуть центральные оси, чтобы они стали главными. Отрицательные углы α0 откладываются по ходу часовой стрелки от оси x.
Теперь покажем, что относительно главных осей осевые моменты инерции обладают свойством экстремальности. Вычислим производную от выражения
J x |
(формула 3.29) и приравняем ее к нулю: |
|||||||
1 |
|
|
|
|
|
|
|
|
|
|
dJ x |
= −2J x cos αsin α + 2J sin αcos α − 2J xy cos 2α; |
|||||
|
|
|
1 |
|
||||
|
|
|
dα |
|||||
|
|
|
|
|
(3.33) |
|||
|
dJ x |
|
|
|||||
|
|
|
||||||
|
|
1 |
|
|
= −(J x − J y ) sin 2αo − 2J xy cos 2αo = 0. |
|||
|
|
|
dα |
|
|
|||
|
|
|
|
α=α |
|
|||
|
|
|
|
|
|
|
o |
|
Сравнивая выражения (3.29) и (3.27) устанавливаем, что
dJdαx1 = −2J x1 y1 = 0 .
Таким образом, производная dJx1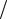 
dα обращается в нуль, когда J x1 y1 = 0 , а
это значит, что экстремальные значения имеют моменты инерции относительно главных осей u и v. Тогда главные центральные моменты инерции определяются по формулам:
|
|
97 |
|
|
Ju |
= J x cos2 αo + J y sin 2 αo − J xy sin 2αo |
(3.34) |
||
J v |
= J x sin 2 |
αo + J y cos2 αo − J xy sin 2αo . |
||
|
||||
Если сложить почленно формулы (3.34), очевидно, Ju + J v = J x + J y = const . Если исключить из (3.34) угол α0 , то получим более удобную формулу для главных центральных моментов инерции:
J minmax |
= |
J x + J y |
± |
1 |
(J x − J y )2 |
+ 4J xy2 . |
(3.35) |
|
2 |
2 |
|||||||
|
|
|
|
|
|
Знак «+» перед вторым слагаемым в (3.35) относится к Jmax , знак «–» – к
Jmin .
Полезно иметь в виду частные случаи:
1 Если фигура имеет две оси симметрии, то оси являются главными цен-
тральными осями.
2 Для правильных фигур – равносторонний треугольник, квадрат, круг и т.п., имеющих более двух осей симметрии, все центральные оси являются главными, а моменты инерции относительно них равны между собой.
Умение находить положение главных центральных осей и вычислять J max и
J min необходимо для определения плоскости наибольшей жесткости сече-
ния (след которой совпадает с осью J min ) при расчетах на изгиб (Раздел 5).
Общий порядок определения главных центральных моментов инерции
Пусть требуется найти положение главных центральных осей и вычислить относительно них моменты инерции для плоского сечения, состоящего из швеллера и полосы (рис. 3.16):
Рис. 3.16
98
1.Выбирают вспомогательные оси – проводят произвольную систему координат xOy.
2.Разбивают сечение на простые фигуры и по формулам (3.5) определяют положение центра тяжести С относительно выбранных вспомогательных осей.
3.Через точку С проводят центральные оси xc и yc параллельно осям простых фигур.
4.Находят моменты инерции простых фигур относительно собственных центральных осей, используя таблицы сортамента (таблицы прокатных профилей, поставляемых металлургическими заводами в соответствии с требованиями ГОСТов) или по формулам, приведенным выше (пункт «Моменты инерции простых фигур»).
5.Определяют моменты инерции простых фигур относительно центральных осей сечения, используя формулы параллельного переноса (3.28).
6.Определяют центральные моменты инерции всего сечения как сумму соответствующих моментов простых фигур, найденных в пункте 5.
7.Вычисляют угол α0 по формуле (3.32) и, поворачивая оси xc и yc на угол
α0 , изображают главные оси u и v.
8.По формулам (3.34) вычисляют Jmax и Jmin .
9.Делают проверку:
а) |
Jx |
+ J y |
C |
= Jmax +J min ; |
|
||||
|
C |
|
|
|
|
|
|
|
|
б) |
Jmax > JxC > J yC |
> Jmin , если J xC > J yC ; |
|||||||
в) |
J uv |
= |
J x |
− J y |
C |
sin 2α0 + J x y |
cos 2α0 = 0 . |
||
|
C |
|
|||||||
|
|
2 |
|
|
|||||
|
|
|
|
|
|
|
C |
C |
|
|
|
|
|
|
|
|
|
||
Контрольные вопросы к разделу 3
1.Что такое статический момент сечения?
2.Дайте определение центральной оси сечения.
3.Дайте определение центра тяжести сечения.
4.Что такое осевые моменты инерции сечения?
5.Что такое центробежный момент инерции сечения?
6.Что такое полярный момент инерции сечения?
7.Что такое главные оси инерции сечения?
8.Дайте определение главных моментов инерции сечения.
9.Дайте определение радиусов инерции сечения.
10.Чему равен статический момент инерции составного сечения?
11.Чему равны моменты инерции составного сечения?
99
12.Какова размерность статического момента сечения?
13.Чему равен статический момент сечения относительно центральной оси?
14.По каким формулам определяются координаты центра тяжести сечения?
15.Для каких сечений при определении центра тяжести достаточно найти только одну координату?
16.Какова размерность моментов инерции сечения?
17.Чему равна сумма осевых моментов инерции сечения относительно взаимно перпендикулярных осей?
18.Чему равен осевой момент инерции прямоугольника и равнобедренного треугольника относительно центральной оси, параллельной их основанию?
19.Чему равны осевые моменты инерции круга и кольца относительно центральных осей?
20.Какие оси называются главными и какие главными центральными осями?
100
Раздел 4 Сдвиг и кручение
Тема 4.1 Сдвиг
Чистый сдвиг
Сдвиг – это такой случай нагружения, при котором в поперечном сечении возникает только поперечная сила Q .
Q = ∫τdA. |
(4.1) |
A |
|
Однородный чистый сдвиг можно получить нагружением пластины, захваченной в жесткие контурные шарнирно соединенные накладки (рис. 4.1, а).
Рис. 4.1
Анализ напряженного состояния при чистом сдвиге
Для всех точек пластины касательные напряжения τ будут равны
τ = |
Q |
, |
(4.2) |
|
A |
|
|
где Q – сдвигающая сила; A – площадь сечения пластины; а касательные на-
пряжения τ принимаем равномерно распределенными по сечению. На гранях выделенного прямоугольного элемента возникают только касательные напряжения (рис. 4.2, б). Такое напряженное состояние называется чистым сдвигом.
Посмотрим, как при чистом сдвиге изменяются напряжения в зависимости от ориентации секущих площадок. Выделим трехгранную призму DCB (рис. 4.1) и рассмотрим ее в равновесии (рис. 4.2).