
u-lectures сопромат
.pdf
161
Эпюра τ
Рис. 5.27
Площадь отсеченной части, расположенной выше сечения:
Aотс. = b(h2 − y);
координата ее центра тяжести:
|
= y + |
( |
h |
− y) |
= 1 (h + y) ; |
|
y |
2 |
|||||
|
|
|
||||
1 |
2 |
2 |
2 |
|||
|
||||||
статический момент отсеченной части относительно нейтральной оси:
|
S отс. |
= y A |
= b |
(h2 |
− y2 ) . |
|
|
|
(5.39) |
||||||||
|
|
x |
|
1 |
отс. |
2 |
|
4 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Подставляя полученные значения в (5.38): |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
τ = |
Q |
S отс. |
|
|
|
|
|
|
|
|
|
|
|||
|
|
y |
x |
|
, |
|
|
|
|
|
|
|
|
|
|
||
|
by J x |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
имеем: |
Qy b 2 (h2 4 − y2 ) |
|
|
6Qy |
|
|
|
|
|
|
|||||||
τ = |
= |
|
(h |
4 |
4 − y |
2 |
). |
(5.40) |
|||||||||
b |
|
b h3 |
12 |
|
|
|
bh3 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
Формула (5.40) показывает, что касательные напряжения по высоте сечения изменяются по закону квадратной параболы (переменная y во второй степени).
При y = ± h/2 в крайних волокнах τ= 0, а при y = 0 на уровне нейтральной оси τmax :
162
τmax = |
3Q |
= |
3Q |
. |
(5.41) |
2bh |
|
||||
|
|
2A |
|
||
На рисунке 5.27, б дан общий вид эпюры τ, знак напряжения τ |
не имеет |
||||
принципиального значения, и его обычно не указывают. |
|
||||
Двутавровое сечение
Характерной особенностью этого сечения является резкое изменение ширины сечения при переходе от стенки к его полке. В основном поперечную силу воспринимает стенка. Максимальные касательные напряжения (в точках нейтральной оси) найдем из выражения
τmax |
= |
Qy |
Sxmax |
, |
(5.42) |
by |
|
||||
|
|
Jx |
|
||
где Sx max – статический момент полусечения относительно нейтральной оси (для прокатных двутавров берется в таблице сортамента, где обозначен Sx);
by = δ0 .
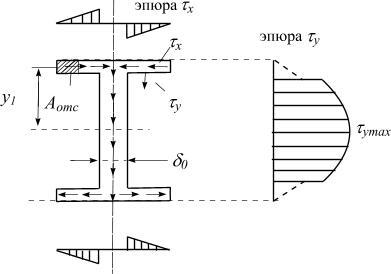
В полках двутавра в каждой точке возникает два касательных напряжения: τy и τx (рис. 5.28). Для вычисления τy нельзя пользоваться формулой (5.38), т.к.
принятые гипотезы здесь оказываются неправильными. Это напряжение вычисляется по формулам теории упругости.
Рис. 5.28
163
Практически τy не влияют на прочность, т.к. τy << τx . Для определения τx можно воспользоваться общей формулой (5.38); при этом Aотс. и y1 берутся так, как показано на рис. 5.28, тогда статический момент
Sxотс. = y1 Aотс.
Вид эпюр τx в полках и τy в стенке показан на рисунке 5.28.
Сопоставление наибольших нормальных и касательных напряжений при изгибе
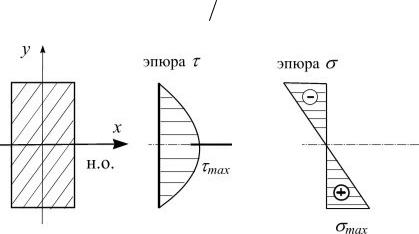
На рис. 5.29 изображены эпюры σ и τ для прямоугольного сечения, из которых видно:
касательное напряжение τmax возникают в тех точках, где σ = 0 (на нейтральной оси);
касательные напряжения τ = 0 в крайних точках сечения, где σmax .
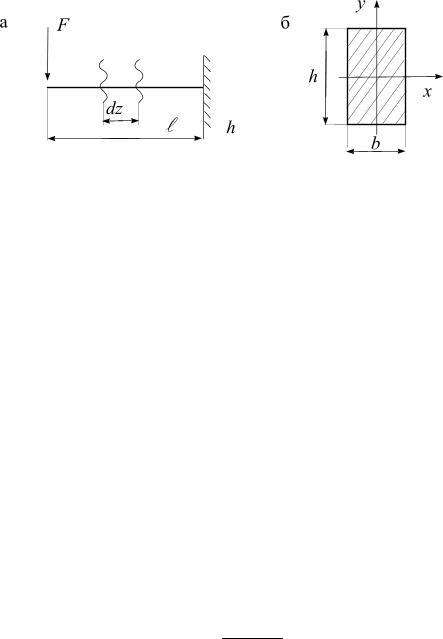
Пусть для балки прямоугольного сечения (рис. 5.30) длина l много больше высоты сечения h. Вычислим наибольшие напряжения по формулам (5.23) и (5.42), учитывая M max = Fl, Qy = F .
σmax |
= |
M max = |
Fl |
|
, |
τmax = |
3F |
. |
b h2 |
6 |
|
||||||
|
|
Wx |
|
|
2bh |
|||
τmax
Рис. 5.29
164
Рис. 5.30
Возьмем их отношение:
σmax = |
6Fl 2 bh |
= |
4l. |
τmax |
bh2 3 F |
|
h |
Следовательно, σmax >> τmax , т.е. нормальные напряжения значительно больше
касательных.
В прокатной и сварной двутавровой балке, имеющей сравнительно большую высоту, касательные напряжения могут быть значительны при условии, что длина балки невелика и загружена она большими сосредоточенными силами, приложенными близко к опорам.
Расчеты на прочность при поперечном изгибе
Условия прочности по касательным напряжениям:
Метод допускаемых напряжений:
τmax = Qmax Sxmax ≤ [τ],
by Jx
где [τ] – допускаемое касательное напряжение
Метод предельных состояний:
τрасч. |
= |
Qрасч. Sxmax |
≤ Rs γc , |
|
|||
|
|
by J x |
|
(5.43)
(5.44)
где τрасч. – максимальное касательное напряжение в опасном сечении балки; Qрасч. – наибольшая по абсолютному значению расчетная поперечная сила; Sx max – статический момент половины сечения относительно нейтральной оси;
165
Jx – момент инерции площади всего сечения; by - ширина сечения на уровне нейтральной оси; RS – расчетное сопротивление материала балки сдвигу; γc –
коэффициент условий работы балки.
Неравенство (5.43) позволяет производить три вида расчета:
1. Проверка прочности (производится непосредственно по указанному неравенству).
2. Подбор ширины прямоугольного сечения балки (проектный расчет) осуще-
ствляется по формуле
|
|
b ≥ |
Qmax Sx |
|
b ≥ |
Qрасч.Sx |
max |
|
3 2Qрасч. |
|
||||||||
|
|
|
max |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
и |
|
|
|
= |
|
|
. |
(5.45) |
|||||
|
|
|
Jx [τ] |
J x Rs γc |
Rs γc h |
|||||||||||||
3. |
Предельная поперечная сила (несущая способность) определяется из |
|||||||||||||||||
неравенства: |
|
|
J x [τ]by |
|
|
|
|
Jx Rs γc |
by |
|
|
|
||||||
|
|
Q ≤ |
|
и |
Q ≤ |
. |
(5.46) |
|||||||||||
|
|
|
Sxmax |
|
Sxmax |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Условия прочности по нормальным напряжениям |
|
||||||||||||||||
|
σ = |
M xmax |
≤[σ] |
и |
σрасч. = |
M расч. |
≤ R γc . |
(5.47) |
||||||||||
|
Wx |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
Wx |
|
|
|
|
|
||||
Для балок сплошного сечения основным является расчет по нормальным на-
пряжениям σ, расчет по касательным напряжениям τ носит вспомогатель-
ный характер.
Для тонкостенных профилей, деревянных и клееных балок обязательно дела-
ется проверка по τ. Если условие (5.43 или 5.47) не удовлетворяется, то подбирают другое сечение.
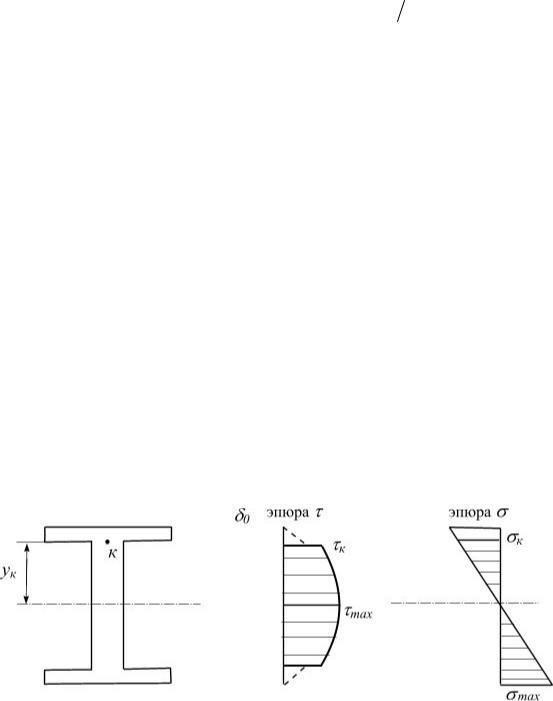
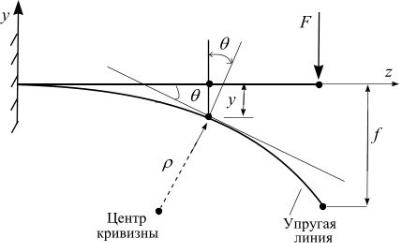
На (рис. 5.31) показаны эпюры σ и τ для двутаврового сечения.
|
|
Эпюра τ |
|
Эпюра σ |
|
||||
|
|
|
|
|
|
|
|
|
|
н.о.
Рис. 5.31
166
У точки К, в месте перехода от полки к стенке, нормальные напряжения σк мало отличаются от σmax . Вместе с тем τк в стенке немногим менее τmax . По-
этому точку К нужно проверить на совместное действие σ и τ, что можно сделать, применив теории прочности.
Дифференциальное уравнение изогнутой оси балок
иего интегрирование для определения перемещений
Вслучае прямого изгиба ось балки искривляется в плоскости действия сил, центры тяжести сечений получают линейные перемещения, а сами сечения поворачиваются (рис. 5.32).
Рис. 5.32
Искривленная ось балки называется изогнутой осью или упругой линией. Допущение о малости перемещений позволяет считать, что линейные пере-
мещения – прогибы y, направлены перпендикулярно продольной оси z недеформированной балки. Наибольший прогиб называется стрелой прогиба и
обозначается f .
Согласно принятому направлению осей координат (рис. 5.32), положительным будем считать прогиб вверх, отрицательным – вниз.
Угол θ , на который каждое сечение поворачивается по отношению к своему первоначальному положению, называется углом поворота сечения. Он может быть определен как угол между касательной к упругой линии и осью z.
Согласно геометрическому смыслу производной tg θ= dy/dz. В связи с малостью деформаций можно полагать tg θ ≈ θ, поэтому можно принять
θ = dy |
(5.48) |
dz |
|

167
Угол поворота сечения равен первой производной от прогиба по абсциссе се-
чения. Прогиб и угол поворота переменны по длине балки, т.е. зависят от абсциссы z.
Уравнение вида y = f (z) называется уравнением упругой линии балки. Умение
определять перемещения необходимо для расчетов на жесткость, при расчете статически неопределимых балок, при решении задач динамики. Деформация того или иного сечения балки определяется кривизной изогнутой оси (рис. 5.32), которая определяется формулой (5.20)
1 |
= |
M (z) . |
(5.49) |
ρ |
|
EJ x |
|
Из дифференциальной геометрии зависимость между кривизной плоской кривой и координатами z и y выражается:
1 |
= ± |
d 2 y dz2 |
|
|
|
|
. |
(5.50) |
|
ρ |
[1+ (dy dz)2 ]3 2 |
|||
Приравняв правые части (5.49) и (5.50), получим точное уравнение упругой линии балки.
d 2 y dz2 |
M (z) |
|
|
|
|
= ± |
EJx |
. |
(5.51) |
[1+ (dy dz)2 ]3 2 |
||||
Интегрирование этого нелинейного уравнения сопряжено с большими трудностями. Так как допускаемый прогиб для балок составляет не более 1/200 пролета, то образующиеся при этом углы поворота много меньше 1, тогда
dy |
2 |
dy |
<<1), и выражение 5.51 примет вид |
|
||||
1+ |
|
≈1, |
( |
|
|
|||
dz |
|
dz |
|
|
|
|
||
|
|
|
|
|
d 2 y |
= |
M (z) . |
(5.52) |
|
|
|
|
|
dz2 |
|
EJx |
|
Уравнение (5.52) будем называть приближенным дифференциальным уравнением упругой линии.
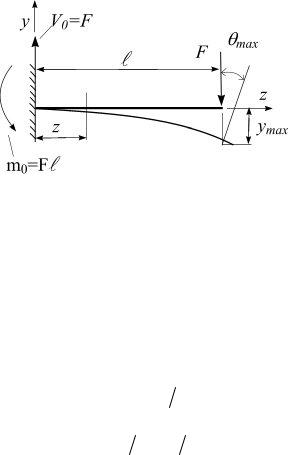
Выбор знака в (5.51) определяется принятой системой координат.
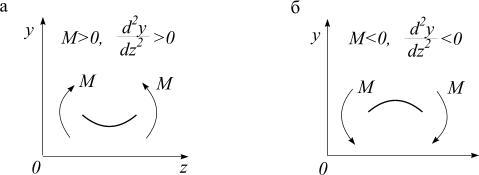
168
Рис. 5.33
Для системы координат, выбранной на рис. 5.33, а,б, знаки изгибающих моментов и второй производной от прогиба совпадают. Таким образом, в (5.51) следует сохранить только «плюс».
Для балки постоянной жесткости EJx = const уравнение (5.52) удобнее записать в виде
EJ x y′′(z) = M (z) . |
(5.53) |
С помощью (5.52) или (5.53) можно вычислять перемещения в балках при любых условиях нагружения.
Углы поворота и прогибы находят последовательным интегрированием дифференциального уравнения упругой линии. После первого интегрирования получается уравнение углов поворота:
EJ x y′(z) = EJ x θ(z) = ∫M (z)dz + C . |
(5.54) |
После второго - уравнение прогибов:
EJ x y( z ) = ∫dz∫M ( z )dz +Cz + D , |
(5.55) |
где С и D – произвольные постоянные интегрирования; их значения опреде-
ляют из граничных условий, т.е. условий опирания балки.
Этот способ определения перемещений называют методом непосредственно-
го интегрирования.
Порядок определения перемещений методом непосредственного интегрирования
Разбивают балку на участки и для каждого записывают выражение изгибающему моменту Мz.
Для каждого участка составляют дифференциальное уравнение, подставляя
169
Мz в (5.53).
Для каждого участка дифференциального уравнение (5.53) дважды интегрируют и получают общие выражения для угла поворота θ (5.54) и прогиба y
(5.55).
Из условий на опорах балки и на границах участков определяют постоянные интегрирования С и D и подставляют в уравнения (5.54) и (5.55).
Определяют θ и у в нужном сечении, подставляя значения z в (5.53) и (5.55).
Пример. Определить наибольший угол поворота и стрелу прогиба для консоли методом непосредственного интегрирования (рис. 5.34); EJ x = const.
Решение. Помещаем начало координат О в заделке. Составляем аналитическое выражение изгибающего момента в сечении z:
M ( z ) = −F ( l − z ).
О
Рис. 5.34
Делая подстановку в (5.53), получаем приближенное дифференциальное уравнение:
′′ |
− z ), |
(5.56) |
EJ x y ( z ) = −F ( l |
||
которое дважды интегрируем |
|
|
EJ x y′(z) = −F (l z − z2 |
2) + C ; |
(5.57) |
EJ x y(z) = −F (l z2 2 − z3 6) + C z + D . |
(5.58) |
|
Для определения постоянных интегрирования используем граничные условия в заделке:
При z = 0 угол поворота y′ = θ0 = 0 ;
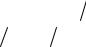
170
При z = 0 прогиб y0 = 0 .
Подставляя эти условия соответственно в (5.57) и (5.58), получим:
EJ xθ0 = C = 0 и EJ x y0 = D = 0 . |
(5.59) |
Откуда постоянные интегрирования С = 0, D = 0.
Окончательно получаем следующие уравнения углов поворота и прогибов:
EJ x y′(z) = EJ x θ(z) = −F (l z − z2 2) , |
|
EJ x y(z) = −F (l z2 2 − z3 6) . |
(5.60) |
Очевидно, что наибольшие значения θ и y достигают на свободном конце. Положив z =l, из (5.60), найдем
θmax |
= − F l2 |
, |
ymax = f |
= − F l3 . |
|
2EJx |
|
|
3EJx |
Знак «минус» в выражении угла поворота показывает, что сечение поворачивается по часовой стрелке; знак «минус» y прогиба означает, что свободный конец опускается.
Примечание. Из выражений (5.59) следует геометрический смысл постоянных интегрирования: они равны соответственно углу поворота и прогибу в начале
координат, умноженному на EJx.
Метод начальных параметров
При интегрировании дифференциального уравнения появляются две произвольные постоянные. Если балка имеет n участков, то требуется составить n уравнений и определить 2n произвольных постоянных. Это весьма трудоемкая задача.
Но если придерживаться определенных правил, то можно добиться равенства постоянных и при любом числе участков получить лишь две постоянные
(5.59):
C = EJ xθ0 и D = EJ x y0 .
Это равенство возможно только тогда, когда в уравнениях моментов при переходе от участка к участку повторяются все члены предыдущего участка, а вновь появляющиеся слагаемые обращаются в нуль на левых границах участков. Для обеспечения этих требований при составлении и интегрировании дифференциальных уравнений должны соблюдаться следующие условия:
Необходимо выбирать единое начало координат на левом конце балки;
При действии распределенной нагрузки, не доходящей до правого конца рас-
