7.3 Трёхфакторный дисперсионный анализ

7.3.1 Общие теоретические соображения

При проведении трёхфакторного дисперсионного анализа начинают с ещё более сложной модели «чёрного ящика» (см. рисунок) исследуемой системы. Здесь рассматриваютсятриодновременно воздействующих на систему фактора: А, В, и С. Каждый из них будет варьироваться на нескольких уровнях: а₁,а₂,а₃,..,а_i, .. ,а_{n ,} b₁,b₂,b₃,….b_j, ...,b_m и c₁,c₂,c₃,..,c_p, .... ,c_k , конкретные значения которых впредь будут обозначаться: а_i, b_jи c_p. Здесь и везде нижеi = 1,2,3, .n; j = 1,2,3, ..m; p = 1,2,3, ..k.

Здравый смысл и очевидные соображения

ИССЛЕДУЕМАЯ подсказывают, что для выявления одновремен-

СИСТЕМА ного влияния факторов А, В и С на величину

Фактор АОтклик Y откликаyследуетнесколько (здесь– n); раз

измерить этот отклик при разныхуровнях фак-

Фактор В тора А (например:а₁,а₂,а₃,....а_n) приодном

Фактор С и том же(например, приb_j) уровне фактора

В и при одном и том же(например, прис_р)

Рис. 7.5уровне фактора С. Получив при этомnштук (y_1jр,y_2jр, y_3jр, y_4jр, ..y_{n jр}), по всей видимости разных, значений отклика, следуетпроделать этоже ещёm-1 раз (изменяя каждый раз уровень фактораBи повторяя каждый развсеуровни фактораA), получив в итоге ужеnm;штук (y_i1р,y_i2р, y_i3р, y_i4р, ...y_imр), разных, значений отклика. И, наконец, проделатьвсе эти последовательности операций ещёn-1 раз, изменяя перед каждым новым циклом эксперимента уровень фактора С. При этом, очевидно, что каждое конкретное значение y_ijриз множества{y_ijр}(теперь уже объёмомN=nmk) измеренных значений отклика будет складываться из реального среднего значения

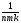
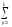
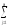
Y~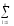y_ijр, прибавки к нему ± Δy_i, обусловленной влиянием (если такое влияние имеет место) фактора А на данном уровне (уровне а_i), такой же прибавки ± Δy_j, обусловленной влиянием (если такое влияние имеет место) фактора В, на очередном (b_j) уровне, прибавки к нему ± Δy_p, обусловленной влиянием (если такое влияние имеет место) фактораCна данном его уровне, (на уровне c_p) и ошибки ±έ_ijp измерительного прибора.

Фиксируем этот факт математически: y_ijp =Y± Δ_i ± Δ_j± Δy_p±έ_ijp. Это равносильно (y_ijp – Y)= (± Δy_i± Δy_j± Δy_p ±έ_ijp) и говорит о том, что дисперсияσ² Генеральной совокупности{y}возможных реальных значение отклика слагается из четырёх составляющих:

- σ_έ² – дисперсии, обусловленной неточностью измерений т.е.ошибкой ±έ_ijp;

- σ_А² – дисперсии, обусловленной ожидаемым влиянием фактора А;

- σ_В² – дисперсии, обусловленной ожидаемым влиянием фактора В;

- σ_C² – дисперсии, обусловленной ожидаемым влиянием фактораC.

Аддитивность дисперсии позволяет записать: σ² = σ_А² + σ_В² + σ_С² + σ_έ²

Таким образом, и здесь, как и раньше, при обработке данных эксперимента встаёт задача разделениясоставляющих общей дисперсии. Способы такого разделения были очень подробно рассмотрены в предыдущих параграфах. Там они позволили нам записать «универсальное соотношение» между общей дисперсией (σ²), дисперсией воспроизводи-мости (σ_έ²) и факторными дисперсиями (σ_А²,σ_В² иσ_С²). Это соотношение при обобщении его на случайS факторов (тогдаразныефакторы удобнее обозначать не разными символами А, В, и С, аодним символом Х сразными индексами,–условными номерами данного фактора в данном эксперименте: Х₁, Х₂, Х₃,..S. В таком случае «универсальное соотношение» выглядит следующим образом:(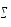_έ) = [СК_∑ –КЧ_i +КЧ_∑]. 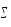Здесь большое (S штук) количество индексов у остаточной суммы квадратов (_έ), связанной с дисперсией воспроизводимости не проставлено – оставлен единственный индекс «_έ», который и означает, что речь идёт о параметре, связанном не с исследуемыми, а со случайными факторами. Индекс «_∑» у всеобщей суммы квадратов (СК_∑) и у квадрата суммы всех значений отклика в эксперименте (КЧ_∑) заменяет те же Sштук индексов 1,2,3, . Sобозначавшие условные номера исследуемых факторов. При не очень большом количествеS исследуемых факторов (у нас их здесь только три) ещё удобнее оставить и «старые» обозначения, например,(Σ₁)=(Σ_А),(Σ₂)=(Σ_В)и(Σ₃)=(Σ_С)