Мартинович Виталий / ОПР

Министерство образования Республики Беларусь

Белорусский Национальный Технический Университет

Кафедра “Системы автоматизированного проектирования”

ОТЧЁТЫ по лабораторным работам

По дисциплине "Оптимизация проектных решений"

Выполнили: студенты гр. 107522

Шиененко В. С.

Мартинович В. В.

Проверил: Ковалева И. Л.

Минск 2015

Лабораторная работа №1 "Построение и исследование графика целевой функции с помощью системы Matlab"

Цель работы:

1.Ознакомиться со способами построения двухмерных и трехмерных графиков.

2. Научиться находить минимальные (максимальные) значения функций, не используя функции программного пакета OptimizationToolbox.

В ходе выполнения лабораторной работы необходимо построить графики заданных функций и исследовать их на минимум, не используя функции программного пакета OptimizationToolbox системы Matlab. Проиллюстрируем выполнение задания на примере следующих функций:

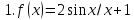→ min на отрезке [0.01;7]

2. → min, переменные x и у определены на отрезке [-5;5]

1. → min на отрезке [-4;4]

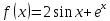2. → min, переменные x и у определены на отрезке [0.1;10]

Для поиска наименьшего элемента в одномерном массиве в Matlab используется функция min. Для того, чтобы определить минимальное значение функции z, используем функцию min(min(z)). Или min (z(:)).

Программный код:

4 вариант

x=0.01:0.001:7;

y=(2*sin(x)./x)+1;

plot(x,y);

[y_min,n]=min(y);

x_min=x(4484);

[x,y] = meshgrid(-5:0.1:5);

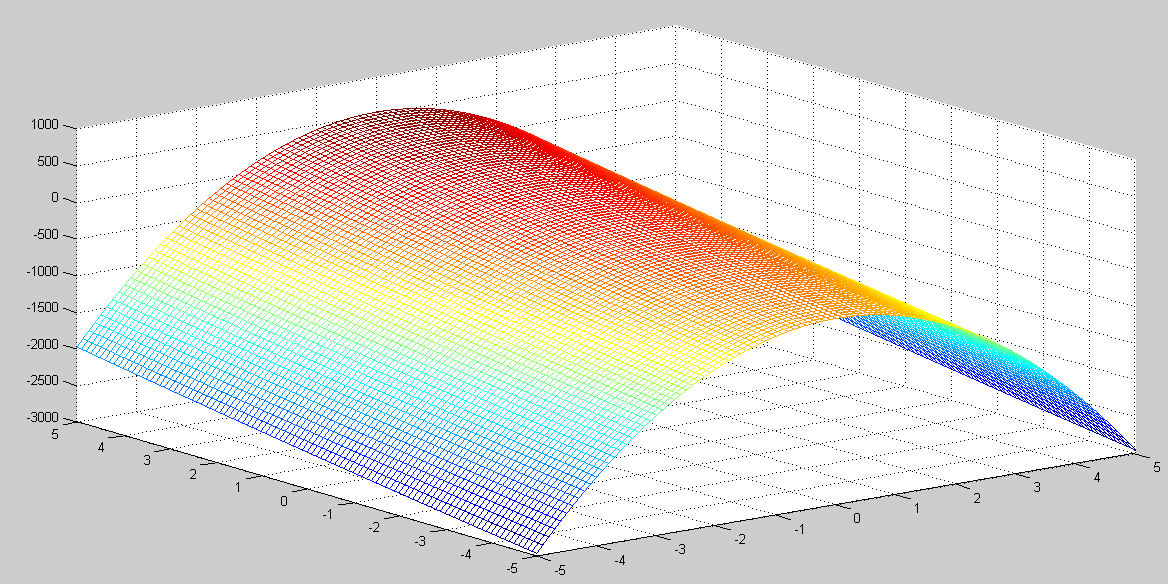
z=(100.*(y-(x.^2)))+((1-y).^2);

mesh(x,y,z)

[x,y] = meshgrid(-5:0.1:5);

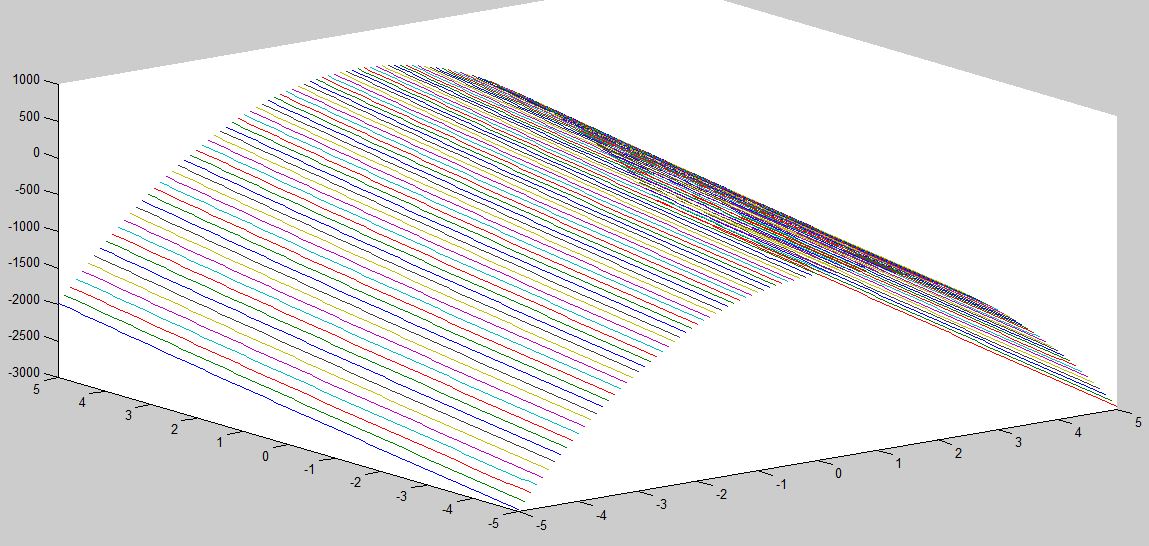
z=(100.*(y-(x.^2)))+((1-y).^2);

meshc(x,y,z)

[x,y] = meshgrid(-5:0.1:5);

z=(100.*(y-(x.^2)))+((1-y).^2);

surf(x,y,z)

[x,y] = meshgrid(-5:0.1:5);

z=(100.*(y-(x.^2)))+((1-y).^2);

plot3(x,y,z)

[x,y] = meshgrid(-5:0.1:5);

z=(100.*(y-(x.^2)))+((1-y).^2);

min_z=min(z(:))

[row_min,col_min]=find(z==min_z)

xx=[-5:0.1:5];

yy=[-5:0.1:5];

xx_min=xx(1);

yy_min=yy(1);

Z=(100.*((-5)-((-5).^2)))+((1-(-5)).^2);

Z

y_min =

0.5655

n =

4484

x_min =

4.4930

min_z =

-2964

row_min =

1

col_min =

1

xx_min =

-5

yy_min =

-5

Z =

-2964

10 вариант

x=-4:0.001:4;

y=(2*sin(x))+exp(x);

plot(x,y);

[y_min,n]=min(y);

x_min=x(2336);

[x,y] = meshgrid(-10:0.5:10);

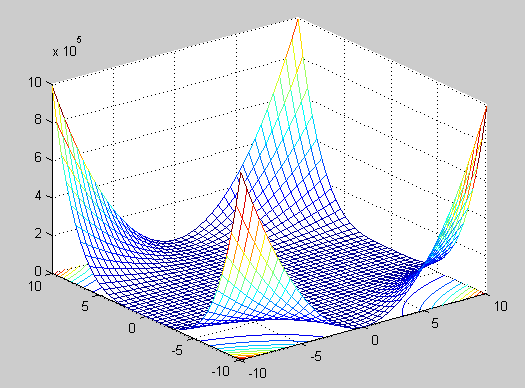
z=((y.*(1-x)).^2)+((1.25-(x.*(1-y.^2))).^2);

mesh(x,y,z)

[x,y] = meshgrid(-10:0.5:10);

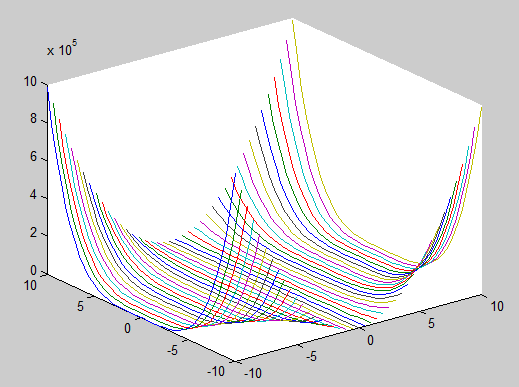
z=((y.*(1-x)).^2)+((1.25-(x.*(1-y.^2))).^2);

meshc(x,y,z)

[x,y] = meshgrid(-10:0.5:10);

z=((y.*(1-x)).^2)+((1.25-(x.*(1-y.^2))).^2);

surf(x,y,z)

[x,y] = meshgrid(-10:0.5:10);

z=((y.*(1-x)).^2)+((1.25-(x.*(1-y.^2))).^2);

plot3(x,y,z)

[x,y] = meshgrid(-10:0.5:10);

z=((y.*(1-x)).^2)+((1.25-(x.*(1-y.^2))).^2);

min_z=min(z(:))

[row_min,col_min]=find(z==min_z)

xx=[-10:0.5:10];

yy=[-10:0.5:10];

xx_min=xx(23);

yy_min=yy(21);

Z=((yy_min.*(1-xx_min)).^2)+((1.25-(xx_min.*(1-yy_min.^2))).^2);

Z

y_min =

-1.8019

n =

2336

x_min =

-1.6650

min_z =

0.0625

row_min =

23

col_min =

21

xx_min =

1

yy_min =

0

Z =

0.0625

Графики:

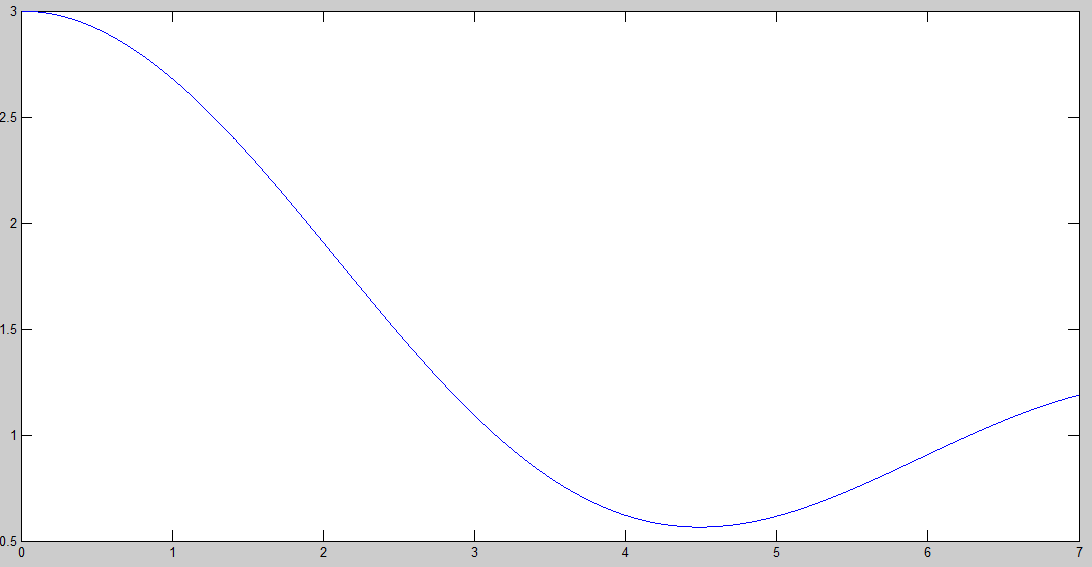
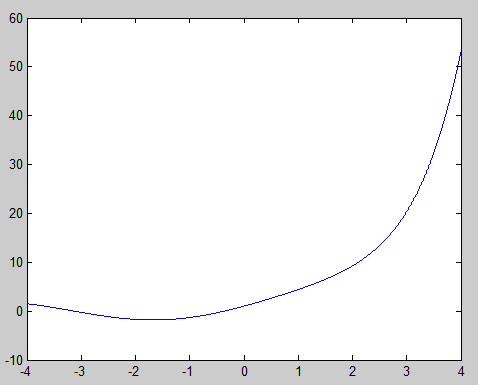
Лабораторная работа №2 "Поиск экстремума целевой функции с помощью программного пакета OptimizationToolbox системы Matlab"

Цель работы:

1.Ознакомиться со способами задания исследуемых функций в системе Matlab.

2. Научиться находить экстремумы функции одной переменной и нескольких переменных, используя наиболее простые функции программного пакета OptimizationToolbox.

Вариант: Метод золотого сечения.

[x, y]=fgoldarea(@vif,0.01,7.0,1000)

x =

4.4935

y =

0.5655

[x, y]=fminbnd(@vif,0.01,7.0)

x =

4.4934

y =

0.5655

[x, y]=fgoldarea(@vaf,-4.0,4.0,1000)

x =

-1.6654

y =

-1.8019

[x, y]=fminbnd(@vaf,-4.0,4.0,1000)

x =

-1.6655

y =

-1.8019

Реализация метода fgoldarea:

function [x_min,y_min] = fgoldarea( funct, a, b, n )

%FRAVNOM Single-variable bounded nonlinear function minimization.

%a-the left boundary

%b-the right boundary

%n-count of numbers

%e-the left boundary

%funct-input function

x1=a+0.382*(b-a);

x2=b-0.382*(b-a);

e=0.000001;

%Calculate the values of the function

A=funct(x1);

B=funct(x2);

for i=0:n

%Set the new range

if(A<B)

b=x2;

%Condition of the count

if(abs(b-a)<e)

%The final calculation of the function's minimum

x_min=(a+b)/2;

y_min=funct(x_min);

else

%Find the new point

x2=x1;

B=A;

x1=a+0.382*(b-a);

%Calculate the values of the function

A=funct(x1);

end

else

a=x1;

if(abs(b-a)<e)

x_min=(a+b)/2;

y_min=funct(x_min);

else

x1=x2;

A=B;

x2=b-0.382*(b-a);

B=funct(x2);

end

end

end

end

Вывод: результаты нашей функции fgoldarea совпадают с результатами встроенной функции fminbnd.

Лабораторная работа №3 "Метод Гаусса"

Реализация метода Gayss:

function [x_min, y_min] = Gaysss( funct, x, n )

[XX,YY] = meshgrid(-15:0.01:15);

ZZ = funct(XX,YY);

hold on;

contour(XX,YY,ZZ,[1,7,13,19,25,40,50,70,90]);

min_x = x;

min_y = 0;

plot([min_x;min_x],[-12;12]);

plot(min_x,-12,'r+:');

for k = 1:n

[min_y]=gayss_ravnommY( funct, min_x );

plot([-12;12], [min_y;min_y]);

plot(min_x,min_y,'r+:');

[min_x]=gayss_ravnommX( funct, min_y );

plot([min_x;min_x], [-12;12]);

plot(min_x,min_y,'r+:');

end

x_min = min_x;

y_min = min_y;

end

Реализация метода gayss_ravnommX:

function [min_x] = gayss_ravnommX( funct, min_y )

b = -12;

zb = funct(b, min_y);

while(b < 12)

b=b+0.05;

z = funct(b, min_y);

if(z < zb)

min_x = b;

zb = z;

end

end

end

Реализация метода gayss_ravnommY:

function [min_y] = gayss_ravnommY( funct, min_x )

b=-12;

zb = funct(min_x, b);

while(b < 12)

b=b+0.05;

z = funct(min_x, b);

if(z < zb)

min_y = b;

zb = z;

end

end

end

Скриншот: