3. Определение уровня воды в напорном баке

Составляем уравнение Бернулли и определяем уровень воды Н в напорном баке:

H = Z₃ + 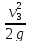+ 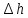=-3,42 + + 13,31 = 10,29 м,

где Z₃ – координата центра тяжести сечения III,

Z₃ = 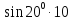= -3,42м

4. Расчёт и построение напорной линии

Полные напоры в сечениях трубопроводов:

Н_а = Н = 10,29 м

Н_в = Н_а — h_вых =10,29 — 0.465 = 9,8 м

Н_с = Н_в —=9,8 — 9,8 = 0 м

Н_d = Н_с —0 — 0,0078 = -0,0078 м

Н_е = Н_d —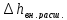=-0,0078 — 0.36 = -0,3678 м

Н_f = Н_е —=-0,3678 — 0,0047 = -0,3725 м

Н_k = Н_f —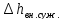=-0,3725 — 0,12 =-0,4925 м

Н_m = Н_k —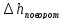==-0,4925 — 0.025 = -0,5175 м

Н_n = Н_m —=-0,5175 — 2.53 = -3.02 м

Результаты расчётов наносим на рис.2

5. Расчёт и построение пьезометрической линии

Скоростные напоры в трубах:

Статические напоры в сечениях трубопроводов:

h_a = Н_а — = 10,29 — 0.93 =9,36 м

h_в = Н_в — 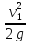= 9,8— 0.93 = 8,87 м

h_с = Н_с — 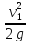= 0 — 0.93 = -0,93 м

h_d = Н_d — 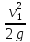= -0,0078— 0.93 = -0,9378

h_е = Н_е — 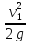= -0,3678 — 0.13 = -0,4978 м

h_f = Н_f — 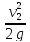= -0,3725— 0.13 = -0,5025 м

h_k = Н_k — = -0,4925 — 0.13 = -0,6225 м

h_m = Н_m — 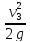=-0,5175 — 0.41 = -0,9275 м

h_h = Н_h — 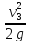= -3,2— 0.41 = -3,61 м

Результаты расчётов наносим на рис. 2

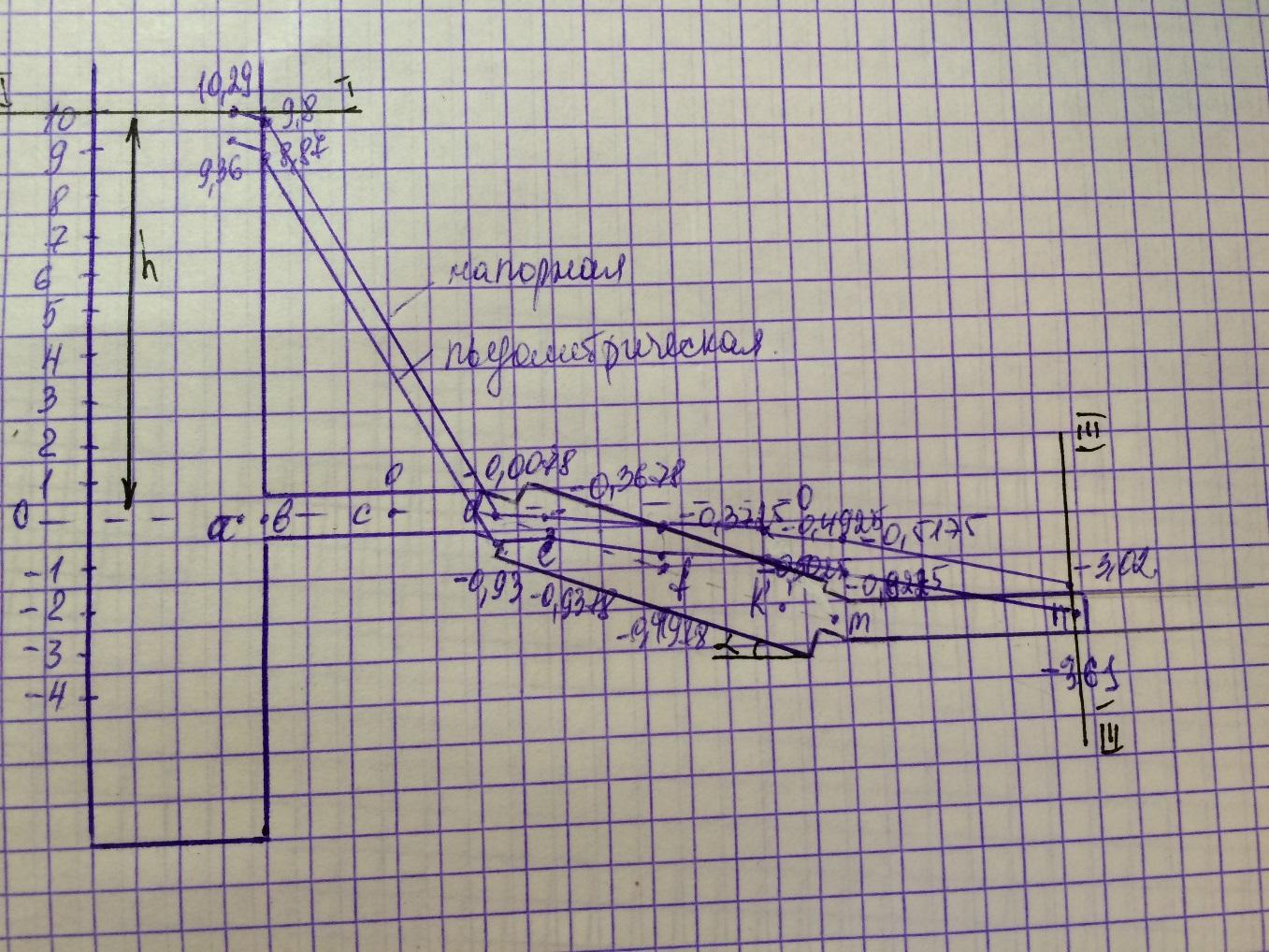
Рис. 2. Напорная и пьезометрическая линии.

6. Расчёт напорной характеристики

Потери в трубопроводах определяются его напорной характеристикой:

где

A - полное гидравлическое сопротивление трубопровода,

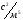
A₁, A₂, A₃ – гидравлические сопротивления отдельных участков трубопроводов.

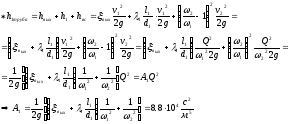
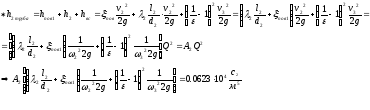
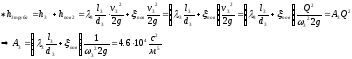
Отсюда 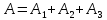=8.8*10⁴+0.0623*10⁴+4.6*10⁴=13.4623*10⁴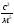

Напорная характеристики трубопровода 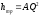=13.4623*10⁴*(8*10^-3)²=8.616м

Задача № 2:Определение высоты всасывания насоса

1. Определение диаметра, средняя скорость всасывающего трубопровода

Из формулы расхода выражаем диаметр трубы:

где Q – расход, – площадь сечения, v – скорость.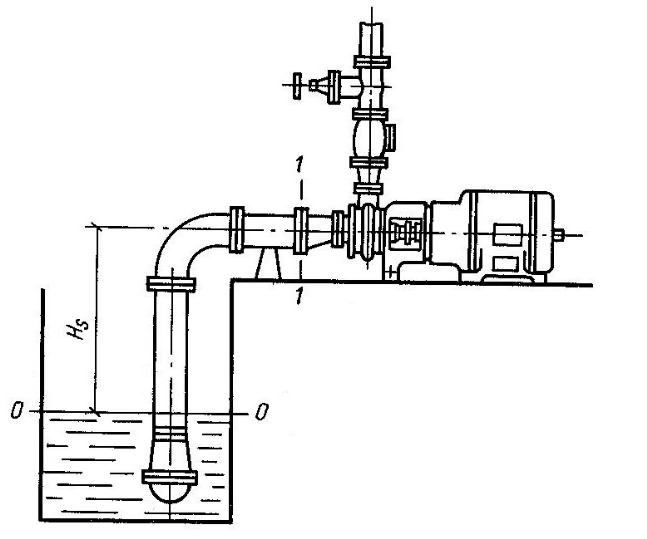

По ГОСТу при диаметре трубы меньшей или равной 250мм, скорость течения в ней воды варьируется от 0.6 до 1 м/с.

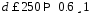
Принимаем диаметр трубопровода равный 100 мм, при заданном расходе вычислим скорость в трубопроводе:

При d = 100 мм

2. Геометрическая высота всасывания:

Для расчета предельной геометрической высоты установки (всасывания) центробежного насоса воспользуемся уравнением Бернулли для сечения 1-1 и 2-2

- коэффициент Кориолиса.

- т.к. высота z₂ соответствует высоте располож.насоса

- т.к. скорость воды в трубопроводе постоянна,

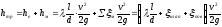
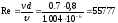
Определим области гидравлического сопротивления, для этого вычислим:

- квадратичная зона

>500

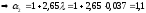
Вычислим предельную высоту установки насоса:

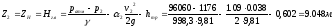
3. Вычислим кавитационный запас:

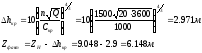
1. Задача №3:потокараспределения в кольцевой трубопроводной сети

Дана схема системы подачи и распределения воды:

Таблица №1

№ участка	Длина участка l, м	Диаметр труб d, мм	Материал	Удельное гидравлическое сопротивление , (л/c)-2	Гидравлическое сопротивление участка , м·(л/c)-2	Расход на участке x, л/с	Потери напора на участке x ΔH, м
1	315	400	чугун	0,2189·10-6	55.76·10-6	133	0,59
2	265	300	чугун	0,9485·10-6	168.7·10-6	133	0,59
3	315	250	чугун	2,528·10-6	665.2·10-6	70,91	1,3
4	415	200	чугун	8,092·-6	2615.5·10-6	48,91	3,99
5	515	150	чугун	37,11·10-6	10062·10-6	15	4,54
6	265	150	чугун	37,11·10-6	5869.5·10-6	5,63	0,41
7	415	200	чугун	8,092·10-6	2615.5·10-6	33,63	3,84
8	265	200	чугун	8,-92·10-6	1830.85·10-6	9,46	0,26
9	315	250	чугун	2,528·10-6	665.2·10-6	62,09	2,96

Таблица №2

Номер узла	Отбор в узле Q, л/c	Давление в узле P, Па	Геод. Отметка z, м	Напор в узле H, м
1	-133	117720	0	15
2	0	778914	0	79,95
3	22,0	759784	0	78,84
4	24,0	733101	0	76,97
5	25,0	618206	0	70,39
6	15,0	624995	0	66,08
7	28,0	687288	0	70,84
8	19,0	737225	0	77,47

Требуется:

1. Рассчитать расход на каждом участке; напор в узлах.

2. Рассчитать потери напора на участках; давление в каждом узле.

3. Рассчитать потери напора по каждому кольцу.

4. Построить напорную линию. Определить пьезометрические уклоны в каждом узле.

Схема системы подачи и распределения воды: в окружностях указаны номера узлов; над дугами – номера дуг; на дуге 1 – насосная станция; направление дуги указывает направление потока

Напорно-расходная характеристика насоса:

1. Получение напоров в узлах и расходов по участкам Получение напоров в узлах и расходов по участкам. Составим уравнение баланса расходов в каждом узле нашей сети.

1. х₁-Q₁=0 х₁=Q₁ х₁ Q₁

2. x₂+x₉ +Q₂-x₁=0 x₂+x₉-x₁=-Q₂ x₂ -Q₂

3. x₃-x₂+Q₃=0 x₃-x₂=-Q₃ x₃ -Q₃

(1) 4. x₄-x₃-x₈+Q₄=0 → x₄-x₃-x₈=-Q₄ x₄ b= -Q₄

5. x₅-x₄-x₆+Q₅=0 x₅-x₄-x₆=-Q₅ x= x₅ -Q₅

6. -x₅+Q₆=0 -x₅=-Q₆ x₆ -Q₆

7. x₆-x₇ +Q₇=0 x₆-x₇=-Q₇ x₇ -Q₇ 8. x₇+x₈+x₉+Q₈=0 x₇+x₈+x₉=-Q₈ x₈ -Q₈ x₉

Построение математической модели кольцевого трубопровода. Составим матрицу полученной системы А (матрица инцинденций).

А
участок узел	1	2	3	4	5	6	7	8	9
1	1	0	0	0	0	0	0	0	0
2	-1	1	0	0	0	0	0	0	1
3	0	-1	1	0	0	0	0	0	0
4	0	0	-1	1	0	0	0	-1	0
5	0	0	0	-1	1	-1	0	0	0
6	0	0	0	0	-1	0	0	0	0
7	0	0	0	0	0	1	-1	0	0
8	0	0	0	0	0	0	1	1	-1

Ах=b

Система линейно-зависима, т.к. ∑Q_i=0 и при сложении всех уравнений системы (1) получили 0=0, поэтому одно уравнение можно вычеркнуть. Получаем усеченную матрицу А и усеченный вектор b.

А
участок узел	1	2	3	4	5	6	7	8	9
1	1	0	0	0	0	0	0	0	0
2	-1	1	0	0	0	0	0	0	1
3	0	-1	1	0	0	0	0	0	0
4	0	0	-1	1	0	0	0	-1	0
5	0	0	0	-1	1	-1	0	0	0
6	0	0	0	0	-1	0	0	0	0
7	0	0	0	0	0	1	-1	0	0

Q₁

-Q₂

-Q₃

b= -Q₄

-Q₅

-Q₆

-Q₇

Тогда уравнение баланса расходов примет вид: Ax=b. (2)

2. Составляем уравнение Бернулли для каждого участка гидравлической системы, например, для первого участка.

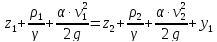
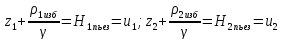
На первом участке получаем следующее уравнение:

u₁-u₂=y₁,

где u₁, u₂ – пьезометрические напоры в 1 и 2 узлах; y₁ - потери напора на первом участке, y₁=y_1длина+y_1насос=S₁|x₁|x₁-H₀-S_H|x₁|x₁=(S₁+S_н)|x₁|x₁-H₀ (потери напора для насоса берутся со знаком «-», т.к. дуга моделирует насос).

Аналогично, составляя уравнения Бернулли для всех остальных участков, получим систему уравнений (3).

1. u₁-u₂=y₁; y₁= (S₁+S_н)|x₁|x₁-H₀ u₁ y₁

2. u₂-u₃ =y₂; y₂=S₂|x₂|x₂ u₂ y₂

3. u₃-u₄ =y₃; y₃=S₃|x₃|x₃ u₃ y₃

4. u₄-u₅ =y₄; y₄=S₄|x₄|x₄ u₄ y₄

(3) 5. u₅-u₆ =y₅; y₅=S₅|x₅|x₅ u= u₅ y= y₅

6. u₇-u₅ =y₆; y₆=S₆|x₆|x₆ u₆ y₆

7. u₈-u₇ =y₇; y₇=S₇|x₇|x₇ u₇ y₇

8. u₈-u₄ =y₈; y₈=S₈|x₈|x₈ u₈ y₈

9. u₂-u₈ =y₉; y₉=S₉|x₉|x₉ y₉

(S₁+S_н)|x₁|x₁

S₂|x₂|x₂

S₃|x₃|x₃

S₄|x₄|x₄

f(x)= S₅|x₅|x₅

S₆|x₆|x₆

S₇|x₇|x₇

S₈|x₈|x₈

S₉|x₉|x₉

Матрица системы (3) является транспонированной матрицей матрицы А.

Выпишем матрицу A^T – транспонированную матрицу.

AT
участок узел	1	2	3	4	5	6	7	8
1	1	-1	0	0	0	0	0	0
2	0	1	-1	0	0	0	0	0
3	0	0	1	-1	0	0	0	0
4	0	0	0	1	-1	0	0	0
5	0	0	0	0	1	-1	0	0
6	0	0	0	0	-1	0	1	0
7	0	0	0	0	0	0	-1	1
8	0	0	0	-1	0	0	0	1
9	0	1	0	0	0	0	0	-1

Тогда в матричном виде получаем:

A^Tu=f(x). (4)

3. Для нахождения неизвестных u и x имеем следующую систему нелинейных уравнений:

Ax=b (2) A^Tu=f(x). (4)

Из составленных уравнений мы получили 9 переменных x и 8 переменных u, всего 9+8=17 – переменных и 7+9=16 - уравнений. Для решения системы уравнений (2) и (4) необходимо задать значение одной из переменных, в данном случае по условию задан напор в первом узле, равный Н₁=25 м. Воспользовавшись программой ИСИГР, находим искомые значения расхода на участке x, потерь напора на участке x, давления в узле и напора в узле и заносим данные в таблицы 1 и 2.

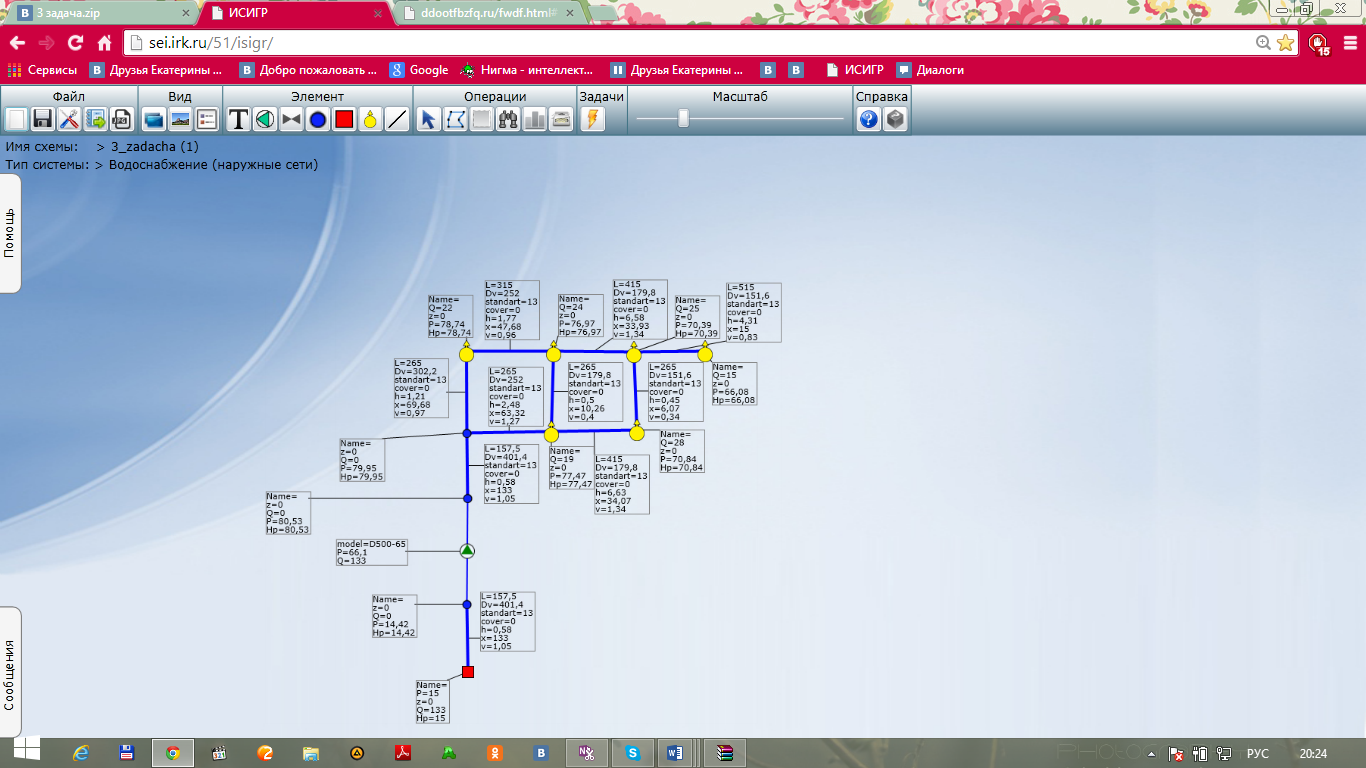
Рис. 6. Схема задачи, решённой в программе ИСИГР

4.Строим пьезометрическую линию трубопровода с 1 до 6 узла, воспользовавшись программой ИСИГР

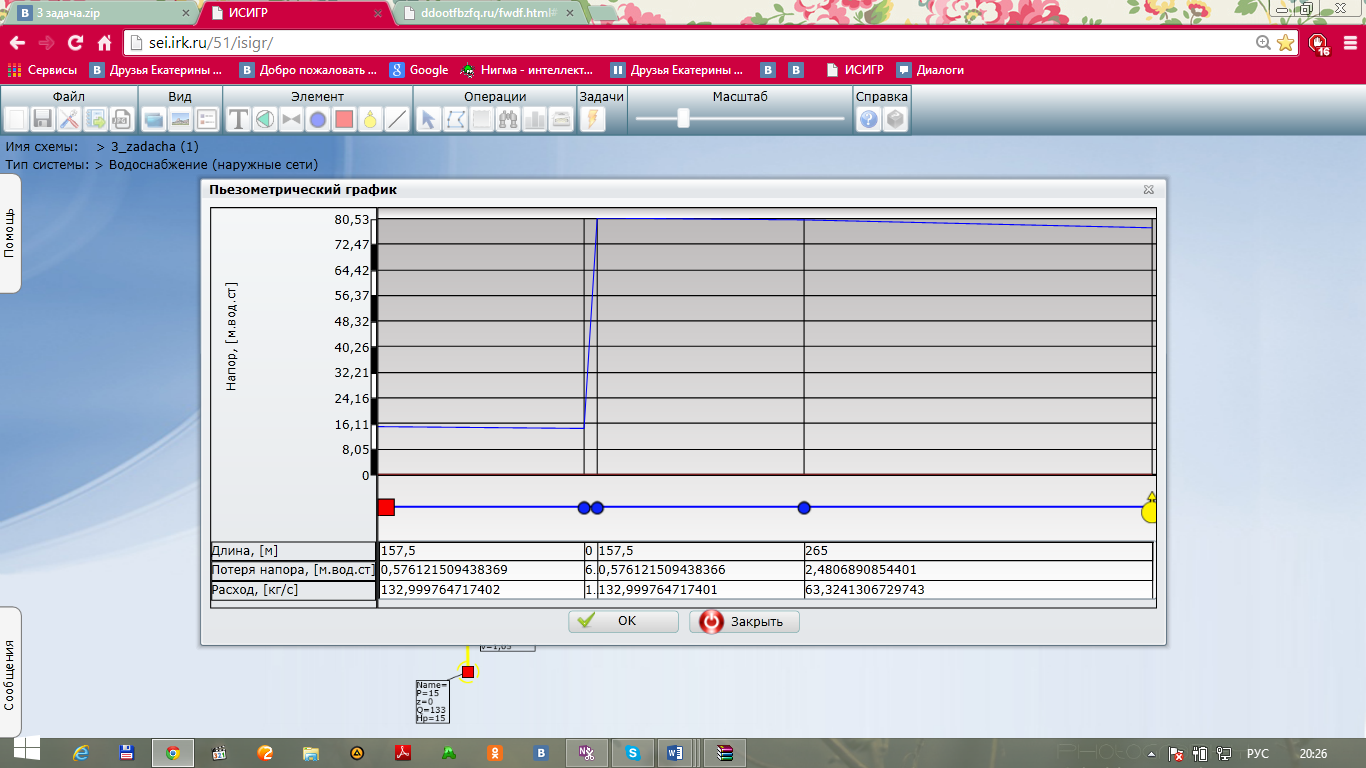
Рис. 7. Напорная характеристика трубопровода с 1 до 6 узла

5. Потери напора по кольцу. Находим алгебраическую сумму потерь напора в кольцах, которая должна быть равна нулю: 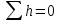.Сеть считается рассчитанной, если при данных расходах по ветвям кольцевой сети потери напора по одной ветви кольца равны потерям напора по другой его ветви.

В нашей сети мы можем выделить три кольца, по которым делаем расчеты.

1. Рассчитаем потери напора по кольцу 2-3-4-8.

Поток в точке 2 разделяется на два направления, а в точке 4 эти потоки сходятся. Отсюда следует, что сумма потерь напора от точки 2 до точки 4 по правой ветви должна быть равна сумме потерь напора между этими точками по левой ветви:

ΔН_{кольцо1} = (Н₂–Н₃) + (Н₃–Н₄) – (Н₈–Н₄) – (Н₂–Н₈) = 0.

Т.е. при рассмотрении движения воды относительно кольца мы принимаем положительными потери напора, возникающие при движении воды по ходу часовой стрелки, а отрицательными – против часовой стрелки.

2. Рассчитаем потери напора по кольцу 4-5-7-8.

Поток в точке 8 разделяется на два направления, а в точке 5 эти потоки сходятся. Отсюда следует, что сумма потерь напора от точки 8 до точки 5 по правой ветви должна быть равна сумме потерь напора между этими точками по левой ветви:

ΔН_{кольцо2} = (Н₈–Н₄) + (Н₄–Н₅) – (Н₇–Н₅) – (Н₈–Н₇) = 0.

3. Рассчитаем потери напора по кольцу 2-3-4-5-7-8.

Поток в точке 2 разделяется на два направления, а в точке 5 эти потоки сходятся. Отсюда следует, что сумма потерь напора от точки 2 до точки 5 по правой ветви должна быть равна сумме потерь напора между этими точками по левой ветви:

ΔН_{кольцо3} = (Н₂–Н₃) + (Н₃–Н₄) + (Н₄–Н₅) – (Н₇–Н₅) – (Н₈–Н₇) – (Н₂–Н₈) = 0.

Сумма потерь напора по каждому кольцу равна нулю.

3. Определение давления в узлах кольцевой цепи

Избыточное давление определяется из определения полного напора:

,

где H_n – напор в соответствующем узле, z_n 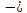геометрическая высота соответствующего узла, удельный вес (= 9,8110³, Н/м³).

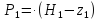= 9,81 10³ (15,00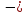0) = 117720 Па;

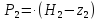= 9,81 10³ (84.930) =778914 Па;

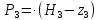= 9,81 10³ (83.63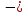0) =759784 Па;

= 9,81 10³ (81.71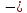0) =733101 Па;

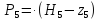= 9,81 10³ (77.72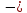0) =618206 Па;

= 9,81 10³ (73.18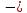0) =624995Па;

= 9,81 10³ (78.130) =687288 Па;

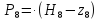= 9,81 10³ (81.970) =737225 Па.

3. Гидравлический уклон

Гидравлический уклон выражает потерю полной удельной энергии (гидродинамического напора), приходящуюся на единицу длины потока.
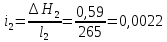
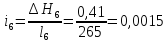
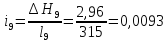