
- •1.Скорости Потока в трубах…………………………………………………….6
- •Задача №1. Расчет коротких трубопроводов.
- •1. Скорости потоков в трубах
- •2. Расчёт потерь напора в трубопроводах
- •3. Определение уровня воды в напорном баке
- •4. Расчёт и построение напорной линии
- •5. Расчёт и построение пьезометрической линии
- •6. Расчёт напорной характеристики
- •Заключение.
- •Список использованной литературы.
Задача №1. Расчет коротких трубопроводов.
 Рис.1.
Схема расположения трубопроводов.
Рис.1.
Схема расположения трубопроводов.
При расчете коротких трубопроводов применяется уравнение Бернулли для двух выбранных сечений и уравнение неразрывности.
Уравнение Бернулли составляется относительно плоскости сравнения, которой может быть любая горизонтальная плоскость. Плоскость сравнения проведена по центру трубы в начале трубопровода.
Расчет необходимо начать с определения формы записи уравнения Бернулли. Для расчета систем водоснабжения и водоотведения обычно применяется уравнение Бернулли в форме напоров:
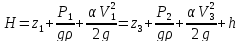 ,
,
где
высота z
называется геометрической высотой, или
высотой положения центра тяжести сечения
струйки;
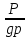 – высота, определяемая величиной
гидродинамического давления, или
пьезометрическая высота;
– высота, определяемая величиной
гидродинамического давления, или
пьезометрическая высота;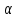 - коэффициент
- коэффициент
Кориолиса;
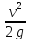 – скоростная высота, или скоростной
напор;
– скоростная высота, или скоростной
напор;
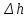 - потери напора.
- потери напора.
Если трубопровод имеет участки с разными диаметрами, то потери напора h при движении жидкости от сечения 1-1 к сечению 3-3 складываются из потерь во всех участках трубопровода. В каждом участке потери разделяются на потери по длине и местные.
1. Скорости потоков в трубах
Скорость потоков в трубах:
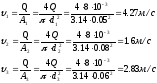
2. Расчёт потерь напора в трубопроводах
Потери
на выходе потока из бака определяется
по формуле
Вейсбаха:
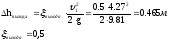
ζвыхода – коэффициент местного сопротивления
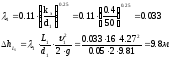
Потери напора по длине рассчитываются по формуле Дарси-Вейсбаха (труба 1):
Для определения потерь напора по длине трубы рассчитаем число Рейнольдса, по рассчитанному числу узнаем режим движения жидкости для всех участков с различными средними скоростями движения жидкости. Коэффициент гидравлического трения λ определяется по формулам, которые выбираются в зависимости от режима движения и области сопротивления.
Найдём число Рейнольдса

Число Рейнольдса определяет характер потока: ламинарный, промежуточный или турбулентный.
ламинарный , если Re <2300
промежуточный, если 2300 < Re <4000
турбулентный, если 4000 < Re
Зависимость коэффициента гидравлического сопротивления от числа Рейнольдса и эквивалентной шероховатости труб
|
Режим (зона) |
Границы |
Коэффициент гидравлического трения | |
|
Ламинарный |
Re<2320 |
| |
|
Турбулентный: | |||
|
1. |
Зона перехода турбулентного движения в ламинарное |
2000<Re<3000 |
|
|
2. |
Зона гидравлически гладких труб |
2320<Re<10d/kэ |
|
|
3. |
Зона смешанного трения или гидравлически шероховатых труб |
10d/kэ<Re<500d/kэ |
|
|
4. |
Зона квадратичного сопротивления (вполне шероховатого трения) |
Re>500d/kэ |
|
Режим
движения жидкости турбулентный, так
как Re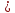 4000. Трубопровод гидравлически шероховатый,
1-
коэффициент гидравлического трения
рассчитывается по формуле Шифринсона:
4000. Трубопровод гидравлически шероховатый,
1-
коэффициент гидравлического трения
рассчитывается по формуле Шифринсона:
Потери напора на повороте:
ζпов.1 = ζ90° (1-cos20°)=0.06 м
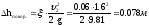
Потери напора при внезапном расширении рассчитывается по формуле Борда:
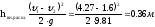
Потеря напора по длине (труба 2):
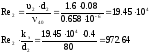
Режим
движения жидкости турбулентный, так
как Re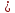 2320.
2320.
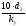
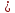 Re
Re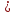
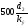 ;
4000 < 194529 < 200000
;
4000 < 194529 < 200000
Трубопровод гидравлически шероховатый.
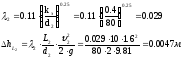
Рассчитаем потери напора при внезапном сжатии:
n — коэффициент сжатия потока
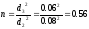
Коэффициент сужения струи находим по формуле Альтшуля:
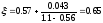
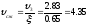
Потерю напора при внезапном сжатии находим по формуле Борда:

Потери напора на повороте:
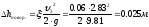
Потери напора по длине (труба 3):
Найдем число Рейнольдса:

Режим
движения жидкости турбулентный, так
как Re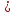 2320. Трубопровод гидравлически шероховатый,
3-
коэффициент гидравлического трения
рассчитывается по формуле Альтшуля.
Потери
напора по длине рассчитываются по
формуле Дарси-Вейсбаха.
2320. Трубопровод гидравлически шероховатый,
3-
коэффициент гидравлического трения
рассчитывается по формуле Альтшуля.
Потери
напора по длине рассчитываются по
формуле Дарси-Вейсбаха.
Рассчитаем суммарные потери напора:
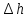 =
=
 = 0,465+9,8+0,36+0,0078+0,0047+0,025+0,12+2,53=13,31м
= 0,465+9,8+0,36+0,0078+0,0047+0,025+0,12+2,53=13,31м

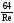 (формула
Стокса)
(формула
Стокса)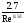 (формула
Френкеля)
(формула
Френкеля)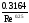 (формула
Блазиуса)
(формула
Блазиуса) (формула
Конакова при Re<3*106)
(формула
Конакова при Re<3*106)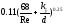 (формула
Альтшуля)
(формула
Альтшуля)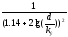 (формула
Никурадзе)
(формула
Никурадзе)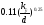 (формула
Шифринсона)
(формула
Шифринсона)