Lab1

Лабораторные работы

1. Изучение функции распределения

случайных величин

Лабораторная работа 1

Экспериментальное определение функции распределения

плотности вероятности результатов измерений

Цель работы: Построение гистограммы результатов измерения и функции распределения плотности вероятности; определение параметров функции распределения.

Приборы и принадлежности: Физический или математический маятник, электрический секундомер.

Методика и техника эксперимента

Величины называются случайными, если в результате опыта вследствие влияния различных случайных причин они могут принимать неодинаковые, но близкие числовые значения. Вероятность случайного события, состоящего, например, в появлении определенной величины а в серии наблюдений, может быть определена как

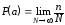, (1)

где n - число наблюдений, при которых появилось событие а;

N - полное число наблюдений;

P(a) - вероятность события а.

Из (1) следует, что вероятность P(a) есть число, значение которого лежит в пределах

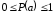. (2)

Событие считается достоверным при P(a) = 1; при P(a) = 0 событие невозможно.

Допустим, что произведено большое число N наблюдений величины а. Получен ряд значений а₁, а₂, ..., а_i, ..., а_N, которые представляют совокупность случайных величин. Результат измерения можно представить графически в виде диаграммы, которая показывает, как часто получаются те или иные значения. Такая диаграмма называется гистограммой.

Для построения гистограммы по оси абсцисс откладывают все значения а_i в порядке возрастания. Далее весь диапазон значений разбивается на одинаковые интервалы а и подсчитывается число значений величины а, попавших в каждый интервал. Величина интервала определяется из выражения

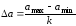, (3)

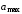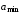где - наибольшее значение измеренной величины,

- наименьшее значение измеренной величины,

k - число интервалов.

Число интервалов берется произвольным, но таким, чтобы в каждом интервале находилось несколько значений а_i.

Пусть в первом интервале 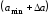оказалось n₁ значений измеренной величины, во втором – n₂ и т.д. Возьмем отношения

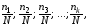
которые приближенно равны вероятности того, что величина a принимает значения, соответствующие первому, второму, ..., . к-му интервалу. Разделив эти величины на ширину интервала а, получим

_{, , ..., , ..., .}

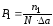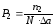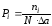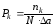Величина

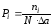(4)

представляет вероятность, приходящуюся на единичный интервал или плотность вероятности, 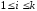. Плотность вероятности не одинакова для разных интервалов, т.е. изменяется с изменением значения a.

Площадь каждого прямоугольника гистограммы с учетом (4) равна

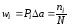
и представляет вероятность того, что величина а лежит в пределах от 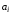до .

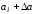При увеличении числа интервалов k до бесконечности величина a стремится к нулю, что возможно только при 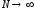, т.е. при бесконечном числе измерений. В этом случае ступенчатая фигура перейдет в плавную кривую f(а), изображенную на рисунке пунктирной линией. Эта функция называется функцией распределения плотности вероятности величины а.

Практика измерений показывает, что результаты измерений и их погрешности часто имеют вид так называемого нормального распределения или распределения Гаусса. Это связано с тем, что экспериментальные данные, полученные при измерении одной и той же величины при воспроизводимых условиях, подчиняются следующим закономерностям:

1. при большом числе наблюдений погрешности равной величины, но разного знака встречаются одинаково часто, т.е. равновероятны;

2. вероятность появления погрешностей уменьшается с ростом величины погрешности, т.е. большие по абсолютной величине погрешности встречаются реже, чем малые.

Аналитическое выражение функции распределения Гаусса имеет вид

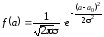, (5)

где а₀ - абсцисса, соответствующая максимуму функции распределения, истинное значение случайной величины;

² - дисперсия - параметр распределения, характеризующий ширину кривой.

В теории вероятности показывается, что параметры функции распределения рассчитываются по формулам:

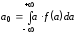, (6)

.

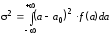Площадь, заштрихованная на графике, численно равна вероятности того, что величина а лежит в интервале от а до .

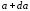Общая площадь по кривыми равна 1:

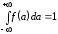, (7)

что соответствует достоверному событию, т.к. означает, что величина а принимает любое возможное значение. Иначе последнее выражение называется условием нормировки функции распределения.

Поскольку дисперсия характеризует разброс результатов относительно истинного значения, то кривая 2 соответствует большей дисперсии, чем кривая 1.

Результаты любого эксперимента являются случайной величиной, которая описывается какой-либо функцией распределения f(а). Если вид f(а) известен, то по формуле (6) можно найти истинное значение и меру разброса результатов - дисперсию.

В реальных условиях f(а) не известна, а число измерений N конечно. Поэтому находят приближенные параметры функции распределения: вместо истинного значения находят среднее арифметическое результатов измерения

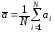, (8)

а вместо дисперсии - ее оценку

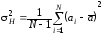. (9)

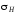также называют среднеквадратичным отклонением наблюдений относительно среднего значения.

При проведении серии измерений получается, что сами средние значения, полученные в результате обработки результатов каждого измерения, являются случайными величинами, разброс которых характеризуется дисперсией для распределения среднего ². В математической статистике показано, что

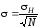. (10)

Следовательно среднеквадратичная погрешность среднего значения рассчитывается по формуле:

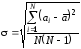. (11)

Среднее значение 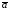отличается от истинного a₀ , причем, величину этой погрешности определить невозможно, т.к. не известно истинное значение a₀. В этом случае задается значение погрешности а такое, чтобы с вероятностью Р абсолютная величина разности между истинным и средним значениями 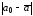не превышала а. Вероятность Р называется доверительной вероятностью, а интервал от 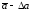до 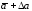- доверительным интервалом.

В качестве результата измерения принимается доверительный интервал, рассчитанный по среднеквадратичному отклонению для распределения среднего и коэффициенту Стьюдента, учитывающему доверительную вероятность и число измерений:

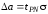. (12)

На лабораторных установках (математический маятник, физический маятник и т.п.) измеряется время 3-5 колебаний. По указанию преподавателя производится 50 наблюдений. Задачей лабораторной работы является построение гистограммы, функции распределения, а также определение параметров функции распределения.

Порядок выполнения работы

1. Произвести 50 измерений времени 3-5 колебаний.

2. Определить наибольшее значение измеренной величины 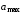и наименьшее значение измеренной величины .

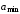3. Разбив весь диапазон значений на 7-8 интервалов, определить ширину интервала а по формуле (3).

4. Записать в таблицу числовые значения границ интервалов.

5. Распределить результаты наблюдений по интервалам.

6. Подсчитать число значений n_i из общей совокупности наблюдений а_i, попавших в каждый интервал.

7. По формуле (4) рассчитать плотность вероятности в каждом интервале.

8. Построить гистограмму распределения плотности вероятности.

9. Провести пунктиром сглаженную кривую функции распределения f(а).

10. По формуле (8) вычислить среднеарифметическое значение .

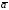11. По формуле (9) рассчитать среднеквадратичное отклонение наблюдений _Н.

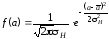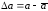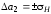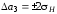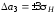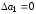
12. Построить функцию распределения Гаусса . Для этого отклонениям от среднего задать значения: , , , . Следует учесть, что при 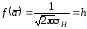и соответствует высоте экспериментальной кривой. В этом случае функция распределения приводится к виду: .

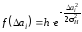13. Сравнить построенную функцию распределения с экспериментальной.

14. Сделать вывод о проделанной работе.

Таблица измерений

	Интервалы
	1	2	3	4	5	6	7
Левая граница
Правая граница
Значения
ni
Рi

Контрольные вопросы

1. Какие величины называются случайными?.

2. Что называют вероятностью случайной величины? Поясните практический смысл вероятности.

3. Дайте определение плотности вероятности, функции распределения.

4. Какие предположения лежат в основе распределения Гаусса?

5. Поясните смысл функции распределения 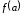и параметра 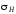. Как от этого параметра зависит форма кривой Гаусса?

6. Что называют доверительной вероятностью и доверительным интервалом?

7. Поясните смысл параметра . Как этот параметр связан с ?

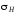7