
ИНФОРМАТИКА-Лабораторные_работы_1_курс / Лаб.4 / Лаб
.4.pdfВычисление пределов, производных, интегралов доступно в Меню «Анализ». Например, вычислим первый замечательный предел («Анализ -> Найти предел»):
limsin x
x 0 x
(%i28) limit(sin(x)/x, x, 0);
(%o28) 1
Для вычисления производной достаточно использовать пункт меню «Анализ -> Дифференцировать», который скрывает в себе функцию diff(Выражение, Переменная), например:
(%i1) f:(x^2)*exp(-x^2);
(%o1) x2 e−x2
(%i2) diff(f, x);
(%o2) 2xe−x2−2x3 e−x2
Для вычисления интеграла нужно использовать пункт меню «Анализ -> Интегрировать».
Например, вычислим интеграл ∫01 ax2 dx |
|
(%i4) y:a*x^2; |
|
(%o4) |
ax2 |
(%i5) integrate(%, x, 0, 1); |
|
(%o5) |
a |
|
3 |
11
Теоретические сведения.
Пусть задан периодический сигнал, который представляет собой последовательность одинаковых импульсов. Форма одного импульса описывается функцией u t . Предположим также, что имеется набор генераторов синусоидальных колебаний, с помощью которых требуется синтезировать заданный сигнал с необходимой точностью.
Для этого нужно сначала исследовать спектр сигнала, затем суммированием несколько первых гармоник с учётом амплитуд и фаз получить аппроксимацию заданного сигнала. Известно, что точно воспроизвести большинство сигналов можно только при использовании бесконечного числа гармоник. Однако на практике такой возможности, как правило, не имеется. Поэтому при синтезе сигнала определённой формы приходится ограничиваться конечным числом спектральных составляющих, что приводит к ошибке аппроксимации. Задавшись приемлемой ошибкой аппроксимации можно найти количество спектральных составляющих для того, чтобы ошибка не была превышена.
В качестве примера рассмотрим сигнал в виде последовательности прямоугольных импульсов. Для математического описания сигнала в виде одиночного импульса введем функцию — индикатор единичной длительности
I x ={1,0, xx 0,50,5}
12
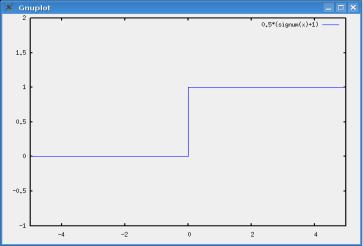
Эту функцию в Maxima можно записать через функцию signum. Для этого введем вспомогательную функцию единичного скачка
q(x):=(signum(x)+1)*0.5
и построим ее график (рис.4)
Рис. 4 Функция единичного скачка
Теперь вводим прямоугольный импульс I(x):=q(x+0.5)-q(x-0.5)
и строим его график (рис. 5)
13
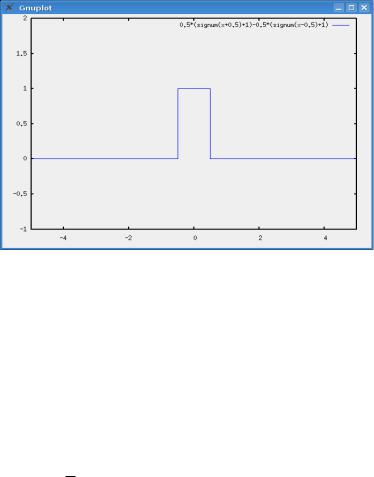
Рис. 5 Прямоугольный импульс
Введём в рассмотрение прямоугольный импульс амплитуды U0 и длительности τ:
U0:2
2
tau:2
2
U(t):=U0*I(t/tau);
U(t) :=U0× Iæ t ö .
ç ÷ èτ ø
Построим график этого сигнала (рис. 6).
14
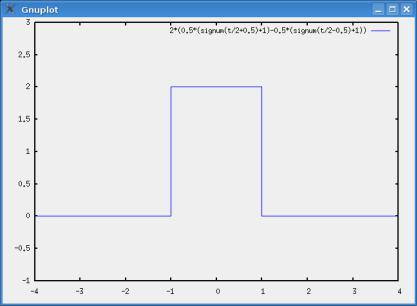
Рис. 6 Прямоугольный импульс амплитуды U0 и длительности τ.
Далее будем рассматривать периодические сигналы. Для этого выполним периодическое продолжение прямоугольного импульса U(t) вправо и влево. Период сигнала должен быть больше его длительности. Будем рассматривать два значения периода, кратные длительности T 0=lτ , T 1=mτ , где l и m заданы в условии ваше-
го варианта. Выберем в качестве примера l=3 , m=5 и введём значения периода как два элемента массива:
15
array(T,float,1);
T[0]=3*tau
T 0=6
T[1]=5*tau
T 1=10
Номер компоненты вектора Т будем далее обозначать переменной i.
Периодическое продолжение прямоугольного импульса К раз в обе стороны от нуля с периодом Т, большим длительности можно выполнить с помощью формулы
K |
|
|
S t ,i ,K := ∑ U t kTi . |
|
|
k=−K |
запишем |
последнюю |
Выберем значение K=3, |
||
формулу в Maxima |
|
|
S(t,m):=sum(U(t+k*T[m]), k, -3, 3)
и построим 2 графика S(t,0) и S(t,1):
plot2d([S(t,0)], [t,-15,15], [y,-1,3], [gnuplot_preamble, "set xrange [-15:15]; set yrange [-1:3];"], [nticks,100])$
plot2d([S(t,1)], [t,-15,15], [y,-1,3], [gnuplot_preamble, "set xrange [-15:15]; set yrange [-1:3];"], [nticks,100])$
В результате получим рис.7 и рис.8 соответственно.
16
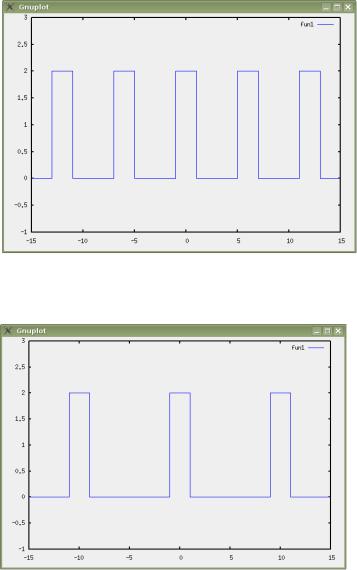
Рис.7 Периодическое продолжение прямоугольного импульса с периодом, равным трем длительностям
Рис.8 Периодическое продолжение прямоугольного импульса с периодом, равным пяти длительностям
17
Находим спектр последовательности импульсов согласно следующим формулам
|
|
|
|
|
τ |
|
|
|
|
|
|
|
|
||||
|
|
2 |
|
|
2 |
|
|
|
|
|
|
2π t |
dt , |
|
|||
an,i = |
|
|
∫ U t cos |
|
n |
|
|||||||||||
|
|
|
|
||||||||||||||
|
T i |
−τ2 |
|
|
|
T i |
|
|
|||||||||
|
|
|
|
|
τ |
|
|
|
|
|
|
|
|
|
|||
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||
bn ,i= |
2 |
∫ U t sin |
n |
2π t |
dt . |
|
|||||||||||
|
|
||||||||||||||||
|
|
T i − |
τ |
|
|
|
|
Ti |
|
|
|
||||||
|
|
2 |
|
|
|
|
|
— син- |
|||||||||
Здесь n — номер гармоники, an, i , bn,i |
|||||||||||||||||
фазная и квадратурная составляющие спектра |
|||||||||||||||||
сигнала с периодом |
T i . В |
|
программе |
Maxima |
|||||||||||||
введём в рассмотрение вспомогательные функции
vsp1(n,i,t):=2*U(t)*cos(2*%pi*t*n/T[i])/T[i]
vsp2(n,i,t):=2*U(t)*sin(2*%pi*t*n/T[i])/T[i] и составляющие спектра
a(n,i):=integrate(vsp1(n,i,t), t, -tau/2, tau/2), b(n,i):=integrate(vsp2(n,i,t), t, -tau/2, tau/2).
График синфазной составляющей спектра a(n,i) как функция n показан на рис.9 синим цветом для i=0, (период последовательности T[0]), красным — для i=1 (период последовательности T[1]).
plot2d([a(n,0),a(n,1)], [n,0,20], [gnuplot_preamble, "set grid;"], [nticks,21])$
Квадратурная составляющая тождественно равна нулю, поскольку исследуемый сигнал четный.
18
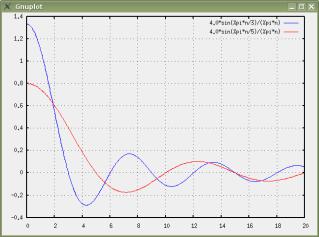
Рис. 9 Синфазная составляющая спектра a(n,i) для двух значений периода сигнала .
Заметим, что по оси абсцисс на рис. 9 отложены номера отсчетов n, а не частоты. Частота каждого отсчета вычисляется по формуле
n,i=2 n/T [i] .
Поэтому на первый взгляд кажется, что спектры сигналов с разным периодом имеют разную ширину. На самом деле разным оказывается масштаб оси абсцисс. Построим теперь синфазную составляющую спектра как функцию частоты. Для этого введем частоту
w(n,i):=2*%pi*n/T[i];
и воспользуемся параметрическим графиком (для удобства восприятия команда разделена на строки)
19
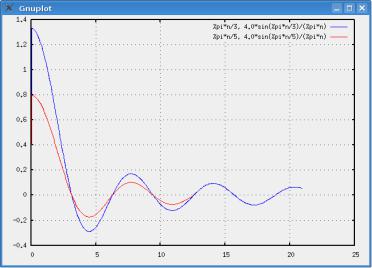
plot2d(
[
[parametric, w(n,0), a(n,0), [n, 0, 20]], [parametric, w(n,1), a(n,1), [n, 0, 20]] ],
[nticks,300], [gnuplot_preamble, "set grid"]
)
Рис. 10 Синфазная составляющая спектра a(n,i) для двух значений периода сигнала как функция частоты.
20
