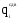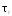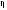2 Проверочный расчёт крыла
2.1Расчёт на изгиб методом редукционных коэффициентов В.Н. Беляева
Крыло изгибается
моментом
 в плоскости
в плоскости .
Это сечение отнесём к произвольной
системе координат
.
Это сечение отнесём к произвольной
системе координат .
Обозначим в произвольной системе
координат
.
Обозначим в произвольной системе
координат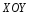 через
через и
и координаты центра масс сечения, а через
координаты центра масс сечения, а через и
и -
координаты центров масс поясов лонжеронов
и стрингеров, которые совместно с
присоединённой обшивкой воспринимают
изгибающий момент. Задаемся редукционные
коэффициенты первого приближения для
всех элементов:
-
координаты центров масс поясов лонжеронов
и стрингеров, которые совместно с
присоединённой обшивкой воспринимают
изгибающий момент. Задаемся редукционные
коэффициенты первого приближения для
всех элементов:
а) для поясов
лонжеронов
 ;
;
б) сжатую обшивку
присоединим к стрингерам в виде полос
шириной
 ;
;
в) для сжатых
стрингеров с присоединённой обшивкой
берём редукционный коэффициент первого
приближения
 ,
(т.к. материал стрингеров и лонжеронов
одинаков, для стрингеровD16T,
для лонжеронов D16T)
считаем, что они не теряют устойчивость;
,
(т.к. материал стрингеров и лонжеронов
одинаков, для стрингеровD16T,
для лонжеронов D16T)
считаем, что они не теряют устойчивость;
Вычисляем приведённые площади сечения первого приближения по формуле:
 .
.
Находим главные центральные оси сечения:
а) в произвольных
осях координат
 определяем координаты центров тяжести
всех элементов редукционного сечения
в первом приближении
определяем координаты центров тяжести
всех элементов редукционного сечения
в первом приближении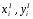 .
.
б) определяем центр масс редуцированного сечения в первом приближении:
 .
.
в) вычисляем
координаты центров тяжести элементов
 в новых главных осях, параллельных
прежним, допуская, что угол поворота
главных осей невелик
в новых главных осях, параллельных
прежним, допуская, что угол поворота
главных осей невелик

г) определяем характеристики сечения в новых главных осях:
 .
.
д) рассчитываем напряжения первого приближения для всех элементов по формуле:
 ,
,
где
 -
коэффициент, учитывающий несимметричность
крыла.
-
коэффициент, учитывающий несимметричность
крыла.
Результаты расчета сведём в таблицу 4 (Приложение А).
2.2 Определение касательных напряжений от сдвига
Расчёт начинаем с выбора основной системы конструкции: сделаем разрезы по хорде от носка крыла, которые превращают сечения в открытый контур рисунок. 1.

Рисунок 1
В местах разрезов
прикладываем замыкающие интенсивности
 и
и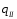 (погонные касательные усилия
(погонные касательные усилия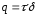 ),
уравновешивающие поперечную силу
),
уравновешивающие поперечную силу ,
приложенную в центре жёсткости крыла.
Поперечная сила, обусловливающая
изгибающий момент, вызывает так же сдвиг
и кручение сечения.
,
приложенную в центре жёсткости крыла.
Поперечная сила, обусловливающая
изгибающий момент, вызывает так же сдвиг
и кручение сечения.
Расписываем погонные касательные усилия в панелях контура:
 ,
,
где
 - касательные потоки в открытом контуре;
- касательные потоки в открытом контуре;
 -
замыкающие погонные потоки (
-
замыкающие погонные потоки ( принимает значения
принимает значения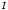 и
и ).
).
Погонная касательная
сила в любой панели при сдвиге замкнутого
контура равна погонной касательной
силе в том же незамкнутом контуре, плюс
замыкающие погонные силы ( ),
причём каждая замыкающая сила добавляется
только на тех панелях контура, которые
являются элементом, замыкающим его.
),
причём каждая замыкающая сила добавляется
только на тех панелях контура, которые
являются элементом, замыкающим его.
Замыкающие погонные
потоки
 определяются из системы канонических
уравнений для произвольного многосвязного
контура из
определяются из системы канонических
уравнений для произвольного многосвязного
контура из контуров, в данном случае – для
двухсвязного контура:
контуров, в данном случае – для
двухсвязного контура:

где
 .
.
Здесь
 -
длина панели;
-
длина панели;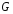 -
модуль упругости
-
модуль упругости рода;
рода; -
толщина панели;
-
толщина панели;
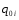 -
погонная сила в панели, возникающая в
незамкнутом контуре.
-
погонная сила в панели, возникающая в
незамкнутом контуре.
Для двухсвязного контура канонические уравнения имеют вид:
 ,
,
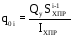 .
.
Здесь
 -
перерезывающая сила в сечении;
-
перерезывающая сила в сечении; -
статический момент относительно оси
всех площадей редуцированного сечения
рассматриваемой части конструкции;
-
статический момент относительно оси
всех площадей редуцированного сечения
рассматриваемой части конструкции; -
момент инерции приведённого сечения
относительно главной центральной оси,
-
момент инерции приведённого сечения
относительно главной центральной оси,
где
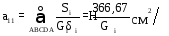 (суммирование ведётся по контуру
(суммирование ведётся по контуру ,
замыкаемому потоком
,
замыкаемому потоком ).
).
 (суммирование
ведётся по контуру
(суммирование
ведётся по контуру
 ,
замыкаемому потоком
,
замыкаемому потоком ).
).

Решаем систему канонических уравнений, зная все коэффициенты.
Зная замыкающие погонные касательные усилия, определяем касательные напряжения в консолях и запас прочности:
 ,
,
 .
.
Все расчеты сведем в таблицу 5 (Приложение Б).
Таким образом, касательные напряжения не превышают разрушающих ни в одной панели, конструкция способна выдерживать заданную нагрузку и хорошо работает на сдвиг.
2.3Определение касательных напряжений от кручения
Кручение конструкции, в результате которого в её нормальном сечении возникают только касательные напряжения, называется свободным. Такое напряжённо-деформированное состояние конструкция испытывает вдали от заделки крыла, от его крепления к фюзеляжу.
Распишем погонные
касательные потоки по панелям сечения
(по аналогии с расчётом на сдвиг), только
здесь в потоках будет отсутствовать
поток в открытом контуре
 .
.
Для определения
неизвестных погонных замыкающих потоков
 составляем канонические уравнения:
составляем канонические уравнения:
 ,
,
 .
.
Коэффициенты
 соответственно равны коэффициентам
канонических уравнений для сдвига.
соответственно равны коэффициентам
канонических уравнений для сдвига.
Третьим уравнением
для определения трёх неизвестных
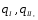 ,
и
,
и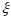 будет уравнение равновесия:
будет уравнение равновесия:
 .
.
В правую часть
уравнения равновесия входит координата
центра жёсткости сечения
 .
.
Координата центра жёсткости сечения определится выражением:
 .
.
Решение уравнения
даёт погонные замыкающие касательные
потоки ,
, .
Зная их, определяем погонные касательные
усилия в панелях контуров, а далее
определяем касательные напряжения:
.
Зная их, определяем погонные касательные
усилия в панелях контуров, а далее
определяем касательные напряжения:
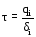 .
.
Расчёт сводится в таблицу 6.
Таблица 6
|
Номер |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
-130 |
1385 |
1255 |
0,08 |
15687 |
21750 |
1,39 |
|
3 |
291 |
1385 |
1675 |
0,08 |
20937 |
21750 |
1,04 |
|
4 |
-1167 |
1385 |
225 |
0,08 |
1875 |
21750 |
11,6 |
|
5 |
198 |
1385 |
1583 |
0,12 |
13192 |
21750 |
1,65 |
|
6 |
191 |
1385 |
1576 |
0,12 |
13133 |
21750 |
1,65 |
|
7 |
184 |
1385 |
1569 |
0,12 |
13075 |
21750 |
1,66 |
|
8 |
176,5 |
1385 |
1561 |
0,12 |
13008 |
21750 |
1,67 |
|
9 |
19 |
1385 |
1404 |
0,12 |
11700 |
21750 |
1,86 |
|
10 |
293 |
1385 |
1678 |
0,12 |
13983 |
21750 |
1,55 |
|
11 |
-49 |
1385 |
1336 |
0,12 |
11133 |
21750 |
1,95 |
|
12 |
-188 |
1385 |
1197 |
0,12 |
9975 |
21750 |
2,18 |
|
13 |
-22 |
1385 |
1363 |
0,12 |
11358 |
21750 |
1,19 |
|
14 |
-206 |
1385 |
1179 |
0,12 |
9825 |
21750 |
2,2 |
|
15 |
-223 |
1385 |
1162 |
0,12 |
9683 |
21750 |
2,25 |
|
16 |
-239 |
1385 |
1149 |
0,12 |
9575 |
21750 |
2,27 |
|
17 |
-231 |
1385 |
1154 |
0,12 |
9617 |
21750 |
2,26 |
|
18 |
-302 |
1385 |
1083 |
0,12 |
9025 |
21750 |
2,4 |
|
19 |
-214 |
1385 |
1171 |
0,08 |
9758 |
21750 |
2,23 |
|
20 |
-198 |
1385 |
1187 |
0,08 |
9892 |
21750 |
2,2 |
Вычисляем величины
касательных критических напряжений и
запас прочности
 :
:
 ,
,
где
 -
коэффициент, учитывающий опирание
панели (
-
коэффициент, учитывающий опирание
панели (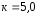 для свободно опёртых краёв и
для свободно опёртых краёв и для защемлённых краёв).
для защемлённых краёв).
 - расстояние между
стрингерами в
- расстояние между
стрингерами в
 ,
,
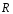 - радиус кривизны
панели в
- радиус кривизны
панели в
 ,
,
 - модуль упругости
- модуль упругости
 рода в
рода в
Заключение
В ходе выполнения работы был произведен расчет классического тонкостенного крыла на изгиб, сдвиг и кручение. Произвели проектировочный расчет для подбора величины площади поперечных сечений силовых элементов. Все вычисления были проведены по самолету Cу-26.
Расчёт конструкции на прочность состоит в определении напряжений, возникающих от нагружения, и сравнения их с разрушающими.
Анализируя результаты вычислений, сведённые в таблице 5, можно сделать вывод, что касательные напряжения не превышают разрушающих ни в одной панели: диапазон запаса прочности от 60 до 100%. Конструкция способна выдерживать заданную нагрузку и хорошо работает на кручение, конструкция в основном спроектирована хорошо.
Список литературы
1 Прочность конструкции. Расчёт крыла А.П. Будник, В.А. Саликов, В.И. Пентюхов, В.И. Максименков. Учеб пособие. Воронеж: Изд-во ВГТУ, 2000, 70 с.
2 Бадягин А.А. Проектирование самолётов. М., 1986.
3 Стригунов В.М. Расчёт самолёта на прочность. М.: Машиностроение, 1984.
4 Строительная механика летательных аппаратов. Под ред. И.Ф. Образцова. М.: Машиностроение, 1986.
5 Астахов М.Ф., Каравлев А.В. Справочная книга по расчету самолета на прочность: справоч. Пособие. – М.: Оборонгиз, 1954. – 702 с.
Приложение А
|
Σ |
|
|
|
|
|
|
-640 |
-2804 |
|
|
|
|
4793 |
|
| |||||
|
18 |
стр. |
1 |
0,8 |
0,9 |
18 |
-33,5 |
-54,3 |
29,2 |
93,16 |
-20,3 |
-75,2 |
-12,2 |
242,7 |
-2399 |
2400 | |||||
|
17 |
стр. |
1 |
0,8 |
0,9 |
41 |
-34,5 |
-55,9 |
66,4 |
93,16 |
-20,3 |
-52,2 |
-13,2 |
284 |
-2595 |
3200 | |||||
|
16 |
лонж. |
2,56 |
0,5 |
1 |
58 |
-35 |
-91 |
150,8 |
93,16 |
-20,3 |
-35,2 |
-13,7 |
490,8 |
-2992 |
3200 | |||||
|
15 |
стр. |
1 |
0,8 |
0,9 |
75,8 |
-35,5 |
-57,5 |
122,8 |
93,16 |
-20,3 |
-17,4 |
-14,2 |
328,5 |
-2791 |
3200 | |||||
|
14 |
стр. |
1 |
0,8 |
0,9 |
99 |
-36 |
-58,3 |
160,4 |
93,16 |
-20,3 |
5,84 |
-14,7 |
352 |
-2889 |
3200 | |||||
|
13 |
стр. |
1 |
0,8 |
0,9 |
123 |
-35 |
-56,7 |
199,3 |
93,16 |
-20,3 |
29,8 |
-13,7 |
305,8 |
-2693 |
3200 | |||||
|
12 |
стр. |
1 |
0,8 |
0,9 |
146,7 |
-34 |
-55 |
237,6 |
93,16 |
-20,3 |
53,5 |
-12,7 |
263 |
-2497 |
3200 | |||||
|
11 |
стр. |
0,5 |
0,4 |
0,9 |
163,2 |
-33,5 |
-6 |
29,4 |
93,16 |
-20,3 |
70 |
-12,2 |
27 |
-2399 |
2400 | |||||
|
10 |
лонж. |
2,4 |
0,4 |
1 |
176,5 |
-33 |
-52,8 |
282,4 |
93,16 |
-20,3 |
83,3 |
-11,7 |
220,5 |
-2557 |
3200 | |||||
|
9 |
лонж. |
2,64 |
0,3 |
1 |
176,5 |
-11,3 |
-33,2 |
527,7 |
93,16 |
-20,3 |
83,3 |
9,96 |
291,7 |
2169 |
2400 | |||||
|
8 |
стр. |
0,5 |
0,3 |
0,9 |
163,2 |
-9,5 |
-1,52 |
26,1 |
93,16 |
-20,3 |
70 |
11,8 |
22,1 |
2305 |
2400 | |||||
|
7 |
стр. |
1 |
0,6 |
0,9 |
146,7 |
-9 |
-13 |
211 |
93,16 |
-20,3 |
53,5 |
12,3 |
216,4 |
2403 |
2400 | |||||
|
6 |
стр. |
1 |
0,6 |
0,9 |
123 |
-8,5 |
-12,2 |
177 |
93,16 |
-20,3 |
29,8 |
12,8 |
234,5 |
2501 |
3200 | |||||
|
5 |
стр. |
1 |
0,6 |
0,9 |
99 |
-8 |
-11,5 |
142,6 |
93,16 |
-20,3 |
5,84 |
13,3 |
253,2 |
2599 |
3200 | |||||
|
4 |
стр. |
1 |
0,6 |
0,9 |
75,8 |
-7,5 |
-10,8 |
109 |
93,16 |
-20,3 |
-17,4 |
13,8 |
272,6 |
2697 |
3200 | |||||
|
3 |
лонж. |
3,84 |
0,3 |
1 |
58 |
-8 |
-34 |
247 |
93,16 |
-20,3 |
-35,2 |
13,3 |
749 |
2888 |
3200 | |||||
|
2 |
стр. |
1 |
0,6 |
0,9 |
41 |
-1- |
-14,4 |
59 |
93,16 |
-20,3 |
-52,2 |
11,3 |
182,6 |
2207 |
2400 | |||||
|
1 |
стр. |
1 |
0,6 |
0,9 |
18 |
-15 |
-21,6 |
25,9 |
93,16 |
-20,3 |
-75,2 |
6,26 |
56,4 |
1227 |
2400 | |||||
|
|
|
Fi |
Fi0 |
Fпр |
|
|
|
|
|
|
|
|
|
|
| |||||
|
Наименование |
Площадь элементов, см2 |
Площадь присоединенной обшивки, см2 |
Приведенная площадь, см2 |
Координаты центра тяж. эл-ов в произв. осях, см |
Приведенные статические Моменты, см3 |
Координаты центра т. редуцированного сечения, см |
Координаты ц.т. эл-ов в новых осях, см |
Осевой момент сечения, см4 |
Напряжения от норм. изгибаа |
Разрушающие напряжения | ||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 | |||||||||
Приложение Б
|
з |
|
-0,075 |
0,17 |
-0,54 |
-0,25 |
-0,06 |
0,12 |
0,3 |
0,32 |
0,61 |
0,37 |
0,37 |
0,35 |
0,15 |
-0,07 |
-0,31 |
-0,54 |
-0,85 |
0,097 |
-0,2 |
|
|
Н/см2 |
-1625 |
3638 |
-9725 |
-543 |
-1292 |
2692 |
6517 |
6925 |
13275 |
8144 |
8142 |
7658 |
3200 |
-1617 |
-6800 |
-11800 |
-18410 |
2110 |
-4325 |
|
|
Н/см |
-130 |
291 |
-1167 |
198 |
191 |
184 |
1765 |
19 |
293 |
-49 |
-188 |
-22 |
-206 |
-223 |
-239 |
-231 |
-302 |
-214 |
-198 |
|
|
см |
0,028 |
0,072 |
0,11 |
0,21 |
0,24 |
0,26 |
0,285 |
0,14 |
0,26 |
0,4 |
0,23 |
0,15 |
0,26 |
0,23 |
0,19 |
0,14 |
0,054 |
0,058 |
0,022 |
|
|
см2/Н |
0,0012 |
0,0011 |
0,0005 |
0,00077 |
0,00077 |
0,00073 |
0,0007 |
0,00035 |
0,00054 |
0,00085 |
0,00054 |
0,00035 |
0,0007 |
0,00073 |
0,00077 |
0,00077 |
0,0005 |
0,0011 |
0,0012 |
|
|
см |
0,08 |
0,08 |
0,08 |
0,12 |
0,12 |
0,12 |
0,12 |
0,12 |
0,12 |
0,12 |
0,12 |
0,12 |
0,12 |
0,12 |
0,12 |
0,12 |
0,12 |
0,08 |
0,08 |
|
|
|
0,8 |
0,8 |
1,2 |
1,2 |
1,2 |
1,2 |
1,2 |
1,2 |
1,2 |
1,2 |
1,2 |
1,2 |
1,2 |
1,2 |
1,2 |
1,2 |
1,2 |
0,8 |
0,8 |
|
|
см |
25 |
22,5 |
12 |
24 |
24 |
23 |
22 |
11 |
14 |
22 |
14 |
11 |
22 |
23 |
24 |
24 |
12 |
22,5 |
25 |
|
|
Н/см |
234 |
655 |
2124 |
2639 |
3136 |
3614 |
4073 |
4122 |
4884 |
4757 |
4268 |
4210 |
3675 |
3097 |
2475 |
1875 |
1082 |
533 |
182 |
|
|
см3 |
9 |
25,2 |
81,7 |
101,5 |
120,6 |
139 |
156,6 |
158,5 |
187,8 |
182,9 |
164,2 |
161,9 |
141,4 |
119,1 |
95,2 |
72,1 |
41,9 |
20,5 |
0,7 |
|
|
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
|
см3 |
9 |
16,2 |
56,5 |
19,8 |
19,1 |
18,4 |
17,65 |
1,9 |
29,3 |
-4,9 |
-18,8 |
-2,2 |
-20,6 |
-22,3 |
-23,9 |
-23,1 |
-30,2 |
-21,4 |
-19,8 |
|
|
см2 |
1,44 |
1,44 |
4,26 |
1,44 |
1,44 |
1,44 |
1,44 |
0,16 |
2,94 |
3,96 |
1,6 |
0,18 |
1,62 |
1,62 |
1,62 |
1,62 |
2,2 |
1,62 |
1,62 |
|
|
см |
6,26 |
11,3 |
13,3 |
13,8 |
13,3 |
12,8 |
12,3 |
11,8 |
9,96 |
-1,24 |
-11,7 |
-12,2 |
-12,7 |
-13,7 |
-14,7 |
-14,2 |
-13,7 |
-13,2 |
-12,2 |
|
№ |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |