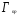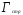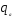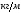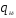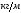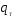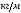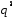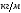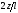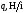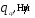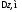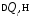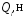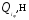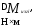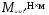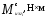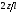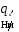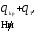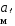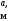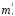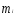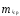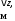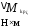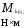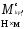1 Предварительный расчет крыла

1. Определение геометрии крыла

,

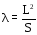где 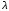-удлинение крыла,

L – размах крыла, м, L=8 м,

S – площадь крыла, м² , S=12 м^2.

,

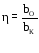где η - сужение крыла

b_o - корневая хорда, м, b_o= 5,43 м,

b_k - концевая хорда, м, b_k=2,5 м.

Удлинение крыла

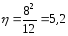
Угол стреловидности: 0⁰

2. Определение нагрузок, действующих на крыло

Нагрузки, действующие на крыло: для заданного случая нагружения определяем коэффициенты безопасности 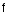и максимальной эксплуатационной перегрузки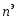. Величины эксплуатационных перегрузок в зависимости от максимального скоростного напора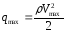и полётной массы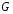определим по таблице типов самолетов.

Для данного типа самолёта принимаем n^э = 8.

Исходя из случая нагружения, коэффициент безопасности выбираем f=2.

Расчётную перегрузку определим по формуле .

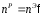Следовательно n^р = 8 × 2 = 16.

Случай 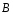соответствует криволинейному полёту с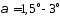(отклоненные элероны или выход из пикирования) и с максимально возможной скоростью, соответствующей скоростному потокуq_max.max. Заданными величинами являются ,;.

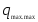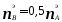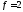Этот случай характерен для нагружения хвостовой части крыла. Вследствие перемещения назад центра давления 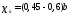на крыло действует значительный крутящий момент.

Расчетная аэродинамическая нагрузка прямого крыла определяется по формуле:

,

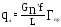где G – вес самолета, кг, G = 17000 кг,

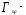относительная циркуляция по размаху прямого крыла, учитывающая изменение коэффициента подъемной силы крыла по размаху и сужению крыла.

Для стреловидного крыла значение 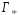должно быть уточнено поправкой, учитывающей стреловидность крыла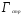. Значения величин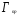и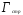снимаем с графиков. Тогда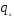рассчитываем по формуле:

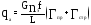
Массовые силы конструкции крыла определяем по формуле:

,

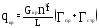где 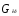- вес крыла,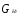= 0,11.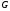

Массовые силы от веса топлива определяем по формуле:

,

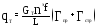где 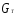- вес топлива,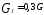,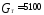кг.

Все расчеты сводим в таблицу 1.

Таблица 1

Величина	2z/l	0	0,1	0,2	0,3	0,4	0,5	0,6	0,65	0,7	0,75	0,8	0,85	0,9	0,95	1
	-	1,24	1,22	1,18	1,15	1,1	1,02	0,9	0,85	0,77	0,65	0,58	0,45	0,34	0,13	0
	-	-0,3	-,018	-0,09	-0,02	0,05	0,1	0,14	0,145	0,15	0,15	0,13	0,11	0,09	0,05	0
	-	0,094	1,04	1,09	1,13	1,15	1,12	1,04	0,995	0,92	0,8	0,71	0,56	0,43	0,18	0
		11186	12367	12971	13447	13685	13328	12367	11841	10948	9520	8449	6664	5117	2142	0
		1118,6	1236,7	1297,1	1344,7	1368,5	1332,8	1236,7	1184,1	1094,8	952	844,9	666.4	511,7	214,2	0
		3355,8	3712,8	3891,3	4034,1	4105,5	3998,4	3712,8	3552,15	3284,4	2856	2534,7	1999,2	1535	642,6	0
		6711,6	7425,6	7782,6	8068,2	8211	7996,8	7425,6	7104,3	6568,8	5712	5069,4	3998,4	3073,2	1285,2	0

По расчетным данным строим эпюру расчетной аэродинамической погонной нагрузки, эпюру расчетной массовой погонной нагрузки, эпюру расчетной суммарной погонной нагрузки (рис. 1).

Рис.1 Эпюры 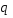,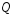и

3. Построение расчетных эпюр

Исходными данными для расчета крыла на прочность являются эпюры перерезывающих сил 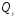, изгибающих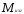и крутящих моментов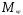, построенные вдоль размаха крыла.

При построении эпюр крыло представляют как двухопорную балку с консолями, нагруженную распределенными и сосредоточенными силами. Опорами являются узлы крепления крыла к фюзеляжу.

Определяем реакции опор:

.

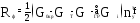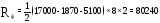кг

Эпюры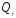,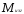нужно строить от суммарной нагрузки

.

Используя дифференциальные зависимости:

; ,

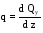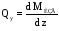получаем выражения 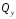и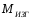для любого сечения крыла:

; .

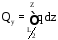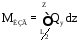Для каждого участка находим приращение перерезывающей силы:

.

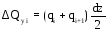Суммируя значения 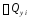от свободного конца и учитывая значения сосредоточенных грузов и реакций фюзеляжа, получаем значение перерезывающей силы в произвольном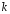- ом сечении крыла

.

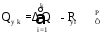Аналогично определяем значение изгибающего момента в любом сечении крыла:

, .

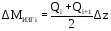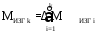Приняв количество сечений i = 10, ∆z = 0,5 м.

С учётом стреловидности крыла перерезывающую силу и изгибающий момент определим по формулам:

; ,

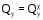где 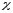- угол стреловидности.

Результаты сведены в таблицу 2.

Таблица 2

0	6711,6	7068,6	0,5	32843	336360	318690	159340	755660	528960
0,1	7425,6	7604,1	0,5	35521	301020	282010	141000	596310	417420
0,2	7782,6	7925,4	0,5	37127	263000	243180	121590	455310	318720
0,3	8068,2	8139,6	0,5	38198	223370	204270	102130	333720	233600
0,4	8211	8103,9	0.5	40520	185170	164910	82455	231583	162110
0,5	7996,8	7711,2	0,5	38556	144650	125370	62686	149130	104390
0,6	7425,6	7265,1	0,5	36326	106090	87930	43966	86442	60510
0,7	6568,8	6140,4	0,25	15351	52676	45000	11250	27170	19019
0,8	5069,4	4533,9	0,25	11335	23840	18180	4547	8273	5791
0,9	3073,2	2185,8	0,25	5441	7048	4327	1082	1283	898

По полученным данным строим эпюру изгибающих моментов (рис.2).

Для построения эпюр крутящих моментов, истинный крутящий момент должен быть определён относительно центра изгиба (жёсткости). Примем координату положения линии центров изгиба (жёсткости):

х_ж = 0,38в_СЕЧ.

Тогда а = 0,2b_СЕЧ, а₁ = 0,4b_СЕЧ.

Погонный крутящий момент в любом сечении относительно линии центров изгиба, оси 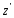определяется следующим образом:

.

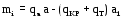Полный крутящий момент будет равен:

.

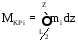При наличии стреловидности :.

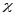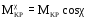Эпюра 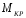строится только до борта фюзеляжа. При определении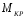также удобно пользоваться методом трапеций с применением таблицы 3:

Где ; .

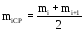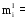
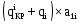Таблица 3

0,2	127910	51884	0,34	0,35	17642	27757	27998	0,5	13999	67752	47426
0,3	134470	53788	0,3	0,33	16136	28239	27531	0,5	13766	53753	37627
0,4	136890	54740	0,26	0,3	14232	26823	24341	0,5	12171	39987	27991
0,5	133280	53312	0,24	0,26	12795	21858	17356	0,5	8678	27816	19471
0,6	123670	49495	0,23	0,24	16828	12853	13872	0,5	6936	19138	13396
0,7	109480	43792	0,21	0,22	9196	14890	12853	0,5	6427	12202	8541
0,8	84490	33796	0,18	0,2	6083	10815	8478	0,5	4230	5775	4043
0,9	51170	20468	0,15	0,18	3070	6140	3071	0,5	1536	1536	1075
1	0	0	0,13	0,15	0	0	0	0,5	0	0	0

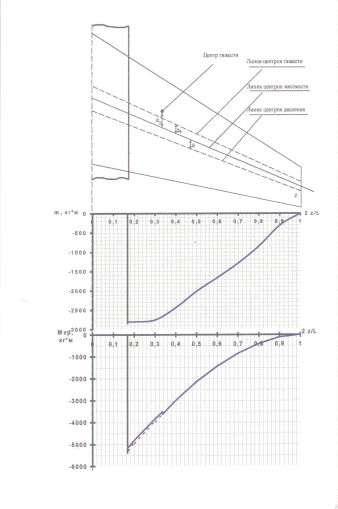
Рис. 2 Эпюры погонного крутящего момента m и крутящего момента .

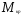4. Проектировочный расчет крыла

На данном этапе подберём величины площади поперечных сечений силовых элементов крыла. Силовая схема крыла – двухлонжеронная, аэродинамический профиль сечения NASA2411 .

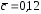Определяем угол конусности крыла:

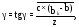
где 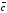-относительная толщина профиля.

Отсюда .

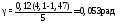Перерезывающая сила в расчетном сечении равна:

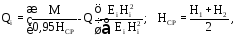
где 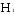и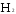-высота первого и второго лонжеронов,

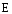- модуль упругости материалов поясов.

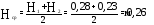
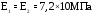
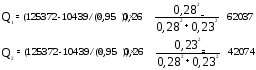
От перерезывающих сил в стенках лонжеронов действуют погонные касательные силы:

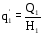и ;

;

.

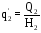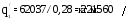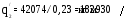Погонные касательные силы в стенках лонжеронов от крутящего момента:

,

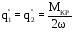где -площадь контура межлонжеронной части сечения.

.

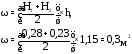
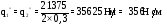Суммарные касательные потоки в стенках лонжеронов от перерезывающих сил и крутящих моментов:

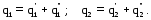
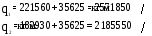
Толщины стенок лонжеронов и обшивки определяются по следующим формулам:

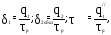
где 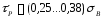- разрушающее касательное напряжение.

Получим

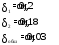
Берем шаг стрингеров 118 мм, получаем количество стрингеров

Определяем силы, действующие на верхней и нижней панелях крыла:

Где 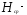высота сечения,

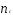- число стрингеров,

- ширина межлонжеронной части крыла.

Коэффициент 0,9 в величине 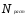учитывает ослабление обшивки отверстиями под заклепки.

Суммарная площадь растянутых и сжатых поясов лонжеронов:

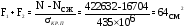- для сжатых поясов,

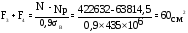- для растянутых поясов,

где 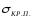принимаем равным.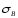