
А.П. Лысенко- Биполярные транзистоы
.pdf
|
21 |
|
JК = |
QA . |
(9) |
|
tA |
|
С учетом (5) - (9) получаем для рекомбинационных потерь в активной базе следующее выражение:
|
WA |
p( x) |
|
|
|
|
∫ |
|
dx |
|
|
|
τ ( x) |
|
|
||
RA = tA |
0 |
|
|
. |
(10) |
WA |
|||||
|
∫ |
p( x)dx |
|
|
|
|
0 |
|
|
|
|
Если пренебречь, в первом приближении, зависимостью времени жизни от координаты и использовать понятие среднего времени жизни в активной базе τА, то рекомбинационные потери в активной базе можно записать в виде:
RA = |
tA |
. |
(11) |
|
|||
|
τ A |
|
|
Для нахождения с использованием выражения (8) необходимо знать распределение инжектированных в активную базу дырок р(х).
2.1.2. Распределение неосновных носителей заряда по координате в активной базе транзистора при произвольном распределении примеси
Учитывая, что в общем случае перенос неосновных носителей через базу транзистора может осуществляться как за счет диффузии, так и за счет дрейфа, для нахождения функции p(x) запишем сначала выражение для тока дырок как функцию координаты х:
J p (x) = qSЭА |
u |
p p(x) (х) – |
qSЭА |
|
|
dp(x) |
JK, |
(12) |
|
D |
|||||||||
p |
dx |
||||||||
|
|
|
|
|
|
|
|
где u p и Dp - усредненные по базе значения подвижности и коэффициента
диффузии неосновных носителей заряда соответственно. Встроенное электрическое поле 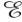 (х) определяется распределением ионизированной примеси (в данном случае эффективной донорной примеси) N(x):
(х) определяется распределением ионизированной примеси (в данном случае эффективной донорной примеси) N(x):

|
|
22 |
|
|
|
|
||
(х) = − |
kT |
1 |
|
dN (x) |
. |
(13) |
||
q |
|
|
N(x) |
|
||||
|
|
|
|
dx |
|
|||
Подставляя (13) в (12), получаем дифференциальное уравнение для определения функции р(х):
dp(x) |
+ |
p(x) dN (x) |
+ |
J K |
|
|
= 0 . |
(14) |
||
|
|
|
|
|
|
|
||||
dx |
N (x) dx |
|
|
|
||||||
|
|
qSЭА Dp |
|
|||||||
Решение этого дифференциального уравнения, при граничном условии р(WA) = 0, имеет вид
р(х) = |
J K |
|
|
1 |
WA |
|
|
|
|
∫N (x)dx . |
(15) |
||||
|
|
|
|
|
|||
qSЭА |
Dp |
|
N (x) |
||||
|
|
x |
|
||||
Получили, что функция р(х), входящая в выражение для
рекомбинационных потерь в активной базе, зависит от распределения по
базе типозадающей примеси и от средней подвижности (т. к. Dp = kTq u p )
неосновных носителей заряда в базе.
2.1.3. Время пролета неосновных носителей заряда через активную базу Рассмотрим, чем определяется время пролета неосновных
носителей заряда через активную базу транзистора.
Для времени пролета в самом общем случае, с учетом (8) и (15)
имеем:
|
1 |
WA |
1 |
WA |
|
|
|||
tA = |
∫ |
∫ |
N (x) dx dx . |
(16) |
|||||
|
|
|
|
||||||
Dp |
|
||||||||
|
0 |
N (x) x |
|
|
|||||
Рассмотрим два наиболее распространенных частных случая.
Случай с однородно легированной базой (бездрейфовый транзистор) и случай с экспоненциальным распределением примеси в базе (дрейфовый транзистор).
Выражение (16) для времени пролета в бездрейфовом транзисторе примет следующий вид:
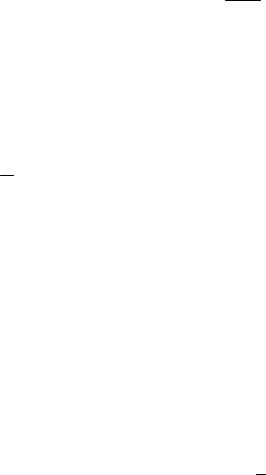
|
23 |
|
|
|
|
W |
2 |
|
|
tA = |
|
A |
, |
(17) |
|
|
|||
|
2DA |
|
||
где с целью унификации обозначений введено понятие DA - коэффициента диффузии неосновных носителей заряда в активной базе.
В случае дрейфового транзистора, если распределение примеси
изменяется с координатой по закону: |
|
N(x) = NБЭ exp(−ax) , |
(18) |
где NБЭ - концентрация примеси в активной базе вблизи эмиттерного перехода (в точке с координатой х=0), а - константа, которую можно найти из условия, что при х=WА концентрация равна NБК, то
|
1 |
|
|
|
|
|
η |
|
|
a = |
|
NБЭ |
|
|
, |
(19) |
|||
|
ln |
|
|
= |
|
|
|||
WA |
|
WA |
|||||||
|
|
NБК |
|
|
|
||||
где введено обозначение η ≡ ln NБЭ . Коэффициент η будем именовать в
NБК
дальнейшем коэффициентом неоднородности легирования базы. Подставляя (18), с учетом (19), в (16), получим для времени пролета:
|
W 2 |
|
|||
tA = |
|
A |
|
, |
(20) |
|
|
|
|||
|
|
||||
|
η DA |
|
|||
где DA - усредненное по активной базе значение коэффициента диффузии неосновных носителей заряда.
Таким образом, время пролета во всех транзисторах пропорционально квадрату толщины активной базы, зависит от типа неосновных носителей (через коэффициент диффузии) и от наличия или отсутствия встроенного электрического поля.
Окончательное выражение для рекомбинационных потерь в активной базе имеет вид:
RA = |
W 2 |
|
|
||
|
|
A |
|
(21) |
|
|
|
|
|
||
η D τ |
|
||||
|
|
|
A |
A |
|
24
Используя общее выражение (15) для распределения неосновных носителей заряда в активной базе, найдем концентрацию инжектированных носителей на границе слоя объемного заряда эмиттерного перехода со стороны базы:
|
JK |
|
|
|
1 |
|
|
W A |
|
|
|
|
|
||||||
р(0) = |
|
|
|
|
|
|
∫N (x)dx . |
(22) |
|||||||||||
qSЭА |
|
|
p |
|
N (0) |
|
|||||||||||||
D |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
Используя теорему о среднем, получим: |
|
|
|
|
|
||||||||||||||
р(0) = |
|
|
|
|
JK |
1 |
|
|
|
|
|
||||||||
|
|
|
|
NA WA , |
(23) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
qSЭА DA |
|
N A (0) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
где с целью унификации обозначений введено понятие NA - концентрации |
|||||||||||||||||||
типозадающей примеси в активной базе. |
|
|
|
|
|
||||||||||||||
Выразим из (23) ток коллектора: |
|
|
|
|
|
||||||||||||||
|
|
qSЭА |
|
|
A p(0)N A |
(0) |
|
|
|||||||||||
JK = |
D |
. |
(24) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
N A WA |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Для низкого уровня инжекции |
NA(0) |
|
= nn0(0), где |
nn0(0)- равновесная |
|||||||||||||||
концентрация основных носителей заряда в базе вблизи эмиттерного перехода. Используя известное граничное условие для p-n- перехода
p(0)n(0) |
= n |
2 |
|
|
|
qV |
|
|
(25) |
||||||||
|
exp |
ЭБ |
|
||||||||||||||
|
|
|
|
|
|
|
|
i |
|
|
|
|
kT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(где VЭБ - напряжение на эмиттерном переходе), получим |
|
||||||||||||||||
|
qSЭА |
|
|
A ni2 |
|
|
qV |
|
|
||||||||
|
D |
|
|
|
|
||||||||||||
JK = |
|
|
|
|
|
|
|
|
|
|
|
exp |
ЭБ . |
(26) |
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
N A WA |
|
|
|
kT |
|
|
|||||||||
Введя обозначение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
qS |
|
|
|
|
|
n2 |
|
|
|
|
|||||
|
ЭА |
D |
|
|
|
|
|||||||||||
|
|
|
|
|
|
A i |
|
≡ Jd , |
|
(27) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
N A WA |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
получим удобное выражение для тока коллектора в виде |
|
||||||||||||||||
|
|
|
|
|
|
|
|
qV |
|
|
|
|
|
(28) |
|||
JK = Jd exp |
ЭБ |
. |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
kT |
|
|
|
|
|
|
||
25
Для конкретного транзистора характеристический ток Jd легко
определяется экспериментально из зависимости |
|
|
|
|
|
|||||||||||||||||||
|
ln(JK ) = ln(Jd ) + |
qVЭБ |
. |
|
|
|
|
|
(29) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kT |
|
|
|
|
|
|
|
|||
Для высокого уровня инжекции, когда |
p(0) >> N |
A |
(0) |
, имеем: |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
qV |
Э− |
Б |
|
|
|
|
|
|
|
|||||
|
p(0) = ni exp |
|
|
|
|
|
|
|
(30) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
2kT |
|
|
|
|
|
|
|
|
||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
qS |
|
|
|
|
|
n |
N |
|
(0) |
|
|
|
qV |
|
|
|
|
|
|
|
|||
J K = |
ЭА |
D |
A |
A |
exp |
Э |
− |
Б |
|
|
|
|||||||||||||
|
|
|
|
i |
|
|
|
|
|
|
. |
|
|
(31) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
N AWA |
|
|
|
2kT |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Не смотря на то, что для высокого уровня инжекции зависимость коллекторного тока от напряжения эмиттер-база другая, чем для низкого уровня инжекции, рекомбинационные потери в активной базе от уровня инжекции в первом приближении не зависят. На самом деле небольшая зависимость есть, т.к. время жизни не сильно зависит от уровня инжекции.
2.1.4. Рекомбинационные потери в пассивной базе Для строгого решения задачи о рекомбинационных потерях в
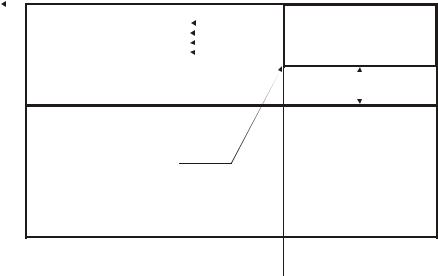
пассивной базе необходимо решать двумерное уравнение непрерывности. Сложности, возникающие на этом пути, не окупают достигаемого результата. Поэтому с точностью, достаточной для инженерных расчетов, рассмотрим упрощенный вариант, представленный на рис. 9, на котором изображен фрагмент пассивной базы. Будем считать, что все носители заряда, инжектированные из эмиттера в пассивную базу, в ней же и рекомбинируют. При этом можно использовать одномерное приближение.
|
26 |
|
|
|
|
|
y |
|
0 |
|
|||
ПБ |
|
|
|
|
p+ |
|
|
|
|
|
|||
|
|
|
||||
|
|
|||||
n |
JП |
|
|
|
|
W A |
|
|
|
|
|||
|
|
|
|
|
||
|
|
|
|
|
|
|
W Э
p
 x
x
Рис.9. Одномерная модель тока JП
Будем считать, что легирование базы в направлении оси y не меняется, а зависит только от х. Поскольку размеры пассивной базы в направлении у, как правило, существенно больше диффузионной длины неосновных носителей заряда, то можно считать, что с бокового торца эмиттерного перехода дырки инжектируются в полу бесконечную среду. Тогда их распределение по координате у будет экспоненциальным:
|
|
|
y |
|
, |
(32) |
|
p ( y) = p(0) exp |
− |
|
|
||||
L |
|||||||
n |
|
|
|
|
|
||
|
|
П |
|
|
|||
|
|
|
|
||||
где LП - диффузионная длина неосновных носителей заряда в пассивной базе. Граничное значение дырок р(0) при у=0 определяется соотношением
qV |
ЭБ |
|
|
|
р(0) = рn0(х) exp |
|
, |
(33) |
|
|
|
|||
|
kT |
|
||
где рn0 - равновесная концентрация дырок в базе, зависящая от координаты х. Все было бы просто, если бы концентрация примеси не зависела от х. Введем понятие средней концентрации примеси в пассивной базе и, соответственно, среднее значение инжектированных носителей.

27
|
|
|
|
(0) = |
1 |
W∫Э p(x) |
|
y=0dx = |
1 |
W∫Э pn0 |
|||||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
p |
||||||||||||||||||
|
|
|
WЭ |
WЭ |
|||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
||||||
|
|
W |
|
|
q VЭБ |
|
|
|
q VЭБ |
|
W |
|
|
|
|||||||
= |
1 |
|
∫Э |
ni2 |
e |
kT |
|
dx = |
ni2 e |
kT |
|
∫Э |
1 |
|
|||||||
WЭ |
|
N |
П |
(x) |
|
W |
Э |
|
N П (x) |
||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
||||
q VЭБ
(x) e kT dx =
|
|
|
|
|
q VЭБ |
|
2 |
1 |
|
|
|||
|
|
|
||||
dx = ni |
|
|
|
e |
kT |
, (34) |
|
||||||
|
|
|
|
|||
|
|
NП |
|
|
|
|
где NП - концентрация типозадающей примеси в пассивной базе.
Зная распределение дырок по координате нетрудно рассчитать, сколько их рекомбинирует в единицу времени во всей пассивной базе и таким образом определить ток JП.
Учитывая, что скорость рекомбинации неравновесных носителей заряда определяется соотношением
r(x, y) = |
p(x, y) , |
(35) |
|
|
τ |
П |
|
где τП - среднее значение времени жизни в пассивной базе, общее количество дырок, рекомбинирующих во всей пассивной базе, будет равно:
SЭП |
∞WЭ |
p |
( |
x, y)dydx , |
|
∫ ∫ |
(36) |
||||
|
τ |
П |
|
||
|
0 0 |
|
|
|
|
где SЭП - площадь эмиттерного перехода, граничащая с пассивной базой. Учитывая, что равновесная концентрация неосновных носителей заряда в пассивной базе крайне мала, ею можно пренебречь и считать, что р(x,y) = pn(x,y). Распределение же концентрации неосновных носителей pn(x,y) с учетом (32), (33) и (34) можно свести к функции одной переменной:
|
|
|
|
|
qVЭБ |
|
|
|
|
y |
|
|
|
2 |
1 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||
p(x, y) = p( y) = ni |
|
|
|
|
|
|
|
||||||
|
|
|
exp |
kT |
|
exp |
− |
|
|
|
. |
(37) |
|
|
|
NП |
|
|
|
|
LП |
|
|||||
Тогда составляющая тока базы, обеспечивающая рекомбинацию в пассивной базе с учетом (37) и (36), будет равна:

|
|
|
|
|
|
|
28 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
qVЭБ |
|
||
|
|
|
|
|
1 |
|
|||||||
J П = |
q SЭП DП ni |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
exp |
|
. |
(38) |
|
|
|
|
|
|
|
|
|
||||||
LП |
|
|
kT |
||||||||||
|
|
|
NП |
|
|
|
|||||||
Теперь, используя выражение для тока коллектора (28), легко определить рекомбинационные потери в пассивной базе:
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
J П |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
N A WA |
1 |
|
|||||||||||||
RП = |
|
q SЭП DП ni |
|
|
|
q SЭП DП ni |
|
|
|
|
|||||||||||||||||||||||
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|||
J |
|
|
|
|
J |
|
|
N |
|
|
|
|
q S |
|
|
|
|
|
n2 |
N |
|
||||||||||||
К |
|
L |
П |
d |
|
|
L |
П |
ЭА |
D |
A |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
П |
|
|
|
|
|
|
|
|
|
i |
|
|
П |
|
||||||||||
|
SЭП |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
DП |
|
|
|
|
WA |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|||||
= |
|
|
|
|
|
|
N |
|
|
. |
(39) |
||||||
|
|
|
|
|
|
|
A |
|
|||||||||
|
SЭА |
DA LП |
|
|
|
|
|||||||||||
|
|
|
N П |
|
|||||||||||||
Посмотрим, какие факторы влияют на величину этих потерь. Во-
первых, влияет соотношение площадей SЭП ; во-вторых, - соотношение
SЭА
|
|
|
|
|
|
|
|
1 |
|
||
|
|
|
|||
концентраций |
|
|
|
; в третьих, - толщина активной базы WA; в |
|
|
|
||||
N A |
|
|
|||
|
|
|
NП |
|
|
четвертых, - диффузионная длина неосновных носителей заряда в пассивной базе τП.
Очевидно, что для повышения коэффициента передачи тока транзистора необходимо воздействовать на перечисленные факторы в сторону снижения рекомбинационных потерь в пассивной базе. Чтобы
уменьшить отношение SЭП = ПЭ WЭ (где ПЭ - периметр эмиттера, WЭ -
SЭА SЭА
глубина залегания эмиттерного перехода), надо уменьшать отношение периметра к площади эмиттера и уменьшать глубину залегания эмиттерного перехода. Известно, что наименьшее отношение периметра к площади имеет круг. Поэтому, с точки зрения минимизации рекомбинационных потерь в пассивной базе, круглая форма эмиттера предпочтительнее квадратной и, тем более, прямоугольной. Хотя с экономической точки зрения это далеко не лучший вариант, т.к. приводит к повышению стоимости транзистора.

29
Если же эмиттер выполнен в виде круга, то его периметр ПЭ = 2πrЭ,
а площадь - SЭА =π r 2 |
. Тогда отношение периметра к площади будет равно |
|||||||
|
|
Э |
|
|
|
|
|
|
2 |
. А отношение площадей: |
SЭП |
= |
2WЭ |
. Таким образом, чем больше |
|||
|
r |
|
|
|||||
|
|
|
S |
ЭА |
|
r |
||
|
Э |
|
|
|
|
Э |
||
линейные размеры эмиттера, тем меньше рекомбинационные потери в пассивной базе.
Следует также отметить, что уменьшение толщины активной базы также способствует уменьшению рекомбинационных потерь в пассивной базе.
Поскольку средняя концентрация примеси в пассивной базе существенно больше, чем в активной, то можно полагать, что высокий уровень инжекции в ней для реальных уровней тока коллектора не наступает. Следовательно, при высоком уровне инжекции в активной базе потери в пассивной базе с учетом (30) оказываются пропорциональны току коллектора:
R |
|
= C |
|
qV |
Э− |
Б |
|
~J |
|
|
|
|
|
|
exp |
|
|
|
, |
(40) |
|||||
П |
П |
2kT |
|
K |
||||||||
|
|
|
|
|
|
|
|
|||||
где СП - коэффициент пропорциональности.
2.1.5. Рекомбинационные потери в эмиттере
Определим рекомбинационные потери в эмиттере RЭ. Согласно
определению RЭ = J И , где, как указывалось, ток JИ обусловлен инжекцией
J К
электронов из базы в эмиттер с их последующей рекомбинацией. Условия рекомбинации для инжектированных электронов будут существенно различны в зависимости от соотношения глубины залегания эмиттерного перехода WЭ и диффузионной длины электронов в эмиттере LЭ. Наиболее просто ток инжекции электронов определяется для двух предельных

30
случаев. Если LЭ << WЭ (хотя бы в три раза), то эмиттер будем считать толстым, а распределение инжектированных электронов экспоненциальным. В этом случае все инжектированные электроны погибнут вследствие рекомбинации, не доходя до омического контакта к эмиттеру. Если выполняется обратное неравенство LЭ >> WЭ, то эмиттер будем считать тонким, а распределение инжектированных электронов линейным. В этом случае основная масса инжектированных электронов погибнет вследствие рекомбинации на самом омическом контакте к эмиттеру, где скорость рекомбинации считается бесконечной. Реально глубина залегания эмиттерного перехода обычно мала: максимум несколько микрон. Однако сам эмиттер сильно легирован (до концентрации (5 1018÷1019) см-3, вследствие чего мала подвижность свободных носителей заряда (и, соответственно, коэффициент диффузии) и мало исходное время жизни. Оба этих фактора сокращают диффузионную длину неосновных носителей заряда. Таким образом, вполне реально встретить случай как с толстым, так и с тонким эмиттером.
2.1.5.1. Рекомбинационные потери в толстом эмиттере Приближенно будем считать, что эмиттер легирован однородно со
средней концентрацией примеси NЭ . Распределение инжектированных носителей (электронов) в этом случае имеет вид
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
||
nЭ (x) = nЭ (0) exp |
− |
|
L |
|
|
, |
(41) |
|
|
|
Э |
|
|
||
где |
nЭ (0) |
= np0 (0) |
qV |
ЭБ |
|
|
exp |
|
- концентрация неравновесных электронов |
||||
|
|
|||||
|
|
|
|
kT |
||
на границе слоя пространственного заряда эмиттерного перехода со стороны эмиттера, LЭ - усредненное по координате х значение диффузионной длины электронов в эмиттере, np0 (0) - равновесная
