
Методы оптимизации и исследование операций для бакалавров информатики. Часть 2
.pdf10 |
Введение |
рование можно рассматривать как частный случай выпуклого. Некоторые лекционные курсы, рассчитанные на чистых математиков, построены именно так, от общего к частному. Однако с практической точки зрения этот подход мало что дает, так как только специфика линейных задач позволяет сконструировать суперэффективные численные методы, подобные симплексному.
Простейшей выпуклой нелинейной задачей является задача
квадратичного программирования (quadratic programming — QP), в которой ищется минимум многомерной квадратичной функции при л и н е й н ы х ограничениях. Применяя условия Куна — Таккера, квадратичную задачу удается свести к линейному программированию и получить точное решение за конечное число шагов.
К сожалению, для более сложных случаев точные конечные методы нахождения решения неизвестны. Вместе с тем существует великое множество приближенных итерационных процедур, основанных на тех или иных предположениях и удачных эвристических приемах.
Традиционно задачи и методы нелинейной оптимизации изучаются от простого к сложному, от частного к общему. Как мы увидим в дальнейшем, значительная доля итерационных процедур основана на сведении многомерного поиска к последовательности шагов поиска вдоль заданного направления, то есть на методах поиска экстремума одномерной функции. Этот класс одномерных задач является далеко не тривиальным и заслуживает подробного рассмотрения. Одномерной оптимизации мы посвятим гл. 10.
Следующий по сложности класс задач относится к случаю, когда ограничения отсутствуют, то есть оптимизируемые переменные могут принимать любые значения. С одной стороны, эти задачи безусловной оптимизации (unconstrained optimization) являются актуальными сами по себе, когда из содержательной постановки следует, что ограничения несущественны. С другой стороны, они создают идейную основу для решения задач с ограничениями.
Введение |
11 |
Проблеме оптимизации без ограничений в мировой литературе посвящены тысячи публикаций, предложены десятки различных методов. В гл. 11 мы приведем их классификацию и рассмотрим несколько наиболее типичных алгоритмов. К сожалению, все они гарантируют нахождение решения (глобального оптимума) только для выпуклых целевых функций с дополнительными условиями, которые трудно проверить на практике. Если же функция имеет сложный невыпуклый рельеф, то итеративная процедура в лучшем случае сойдется к одному из локальных экстремумов.
Невыпуклая оптимизация (nonconvex optimization), даже при отсутствии ограничений, в современной науке остается по большей части terra incognita. Тем не менее, учитывая важность проблемы, мы в конце главы рассмотрим основные подходы и некоторые практические методы решения многоэкстремальных задач.
Наличие ограничений, хоть и выпуклых, существенно усложняет задачу оптимизации. Несмотря на то, что теория Куна — Таккера указывает теоретический путь решения общей задачи выпуклого программирования, на практике решение соответствующих уравнений и неравенств может оказаться непомерно сложным. Поэтому предложен ряд обходных путей, которые в некоторых частных случаях оказываются более простыми. Основные подходы к выпуклой оптимизации с ограничениями (constrained optimization) мы рассмотрим в гл. 12.
Гл. 13 чисто практическая. Она будет полезна тем, кто, столкнувшись с реальной оптимизационной задачей, захочет решить ее с помощью стандартных пакетов прикладных программ.
Гл. 14 уводит изучение проблем оптимизации в другую сторону. Она посвящена оригинальному и чрезвычайно остроумному подходу к решению широкого класса задач, который получил название динамического программирования (dynamic programming).
Его основные принципы, элементарные на первый взгляд, но очень глубокие по сути, демонстрируются на простейших содержательных примерах.
В целом, изложение методов нелинейной оптимизации для ба-
12 |
Введение |
калавров информатики имеет целью показать, как ставятся задачи и как устроены основные алгоритмы их решения. Обладая этими знаниями, можно, столкнувшись в жизни с проблемой поиска наилучшего решения, попытаться формализовать ее и предвидеть те трудности, которые возникнут при практической оптимизации. В принципе, этих знаний достаточно и для того, чтобы реализовать на компьютере простейшие алгоритмы и получить полезные результаты, но при этом нужно иметь в виду, что в реальных условиях приходится учитывать множество нюансов и тонкостей, подбирать оптимальные значения многих параметров. При оптимизации сложных целевых функций с нелинейными ограничениями простыми алгоритмами не обойтись. Поэтому на практике, как правило, пользуются промышленными пакетами прикладных программ, разработанными солидными научными организациями под руководством авторитетных ученых с учетом последних достижений в области теории оптимизации. Однако для того, чтобы пользоваться такими пакетами, нужно знать элементы теории и соответствующую терминологию, в том числе англоязычную.
Глава 9
Теория выпуклого программирования
Общепринятой канонической формы задачи выпуклого программирования нет, мы будем считать стандартной задачу м и н и м и з а ц и и выпуклой целевой функции многих пере-
менных
f (x1, . . . , xn) → min
при о г р а н и ч е н и я х - н е р а в е н с т в а х, заданных набором m в ы п у к л ы х функций
gi(x1, . . . , xn) 0, |
i = 1, . . . , m |
и дополнительных ограничениях |
на н е о т р и ц а т е л ь - |
н о с т ь переменных |
|
x1, . . . , xn 0.
Набор переменных, как и прежде, будем считать векторомстолбцом действительных чисел:
|
x1 |
|
|
|
X = |
. . . |
= (x |
, . . . , x )T , |
|
→− |
1 |
n |
||
|
|
|
|
|
xn

14 Глава 9. Теория выпуклого программирования
с учетом этого задачу выпуклого программирования можно записать в векторном виде
f (−→ |
|
→ |
min, |
|
|
|
X ) |
|
|
||
gi(−→ |
|
0, i = 1, . . . , m, |
(9.1) |
||
→− |
X ) |
|
|
||
|
0. |
|
|
||
X |
|
|
|
||
Изучая теорию линейного программирования, основанную на переборе базисных решений системы линейных уравнений, мы рассуждали в рамках понятий арифметического линейного пространства Rn, то есть использовали чисто алгебраические определения линейной комбинации и линейной зависимости столбцов вещественных чисел без привлечения геометрических понятий: направлений, расстояний, углов. Несмотря на то, что элементы этого пространства назывались векторами и обозначались стрелками, они не понимались как объекты, имеющие направления.
В нелинейном программировании геометрические свойства будут играть важную роль, поэтому дальнейшие построения будут вестись в рамках значительно более сложно организованного евклидова пространства.
9.1. Евклидово пространство
Точечно-векторное евклидово пространство, которое мы для краткости будем называть просто евклидовым пространством En, является многомерным обобщением «обычного» трехмерного геометрического пространства.
В школьной математике в качестве первичного геометрического понятия рассматривалась точка, далее определялись геометрические векторы как упорядоченные пары точек и изучались их алгебраические свойства. Здесь же мы поступим наоборот, взяв за основу знакомое арифметическое линейное пространство со всей его алгебраической аксиоматикой [9, с. 55]. Обогащение его гео-
9.1.. Евклидово пространство |
15 |
метрическими категориями осуществляется в два этапа (см. [10,
c.92]):
•на первом этапе векторное Rn дополняется точечным пространством An, в совокупности они образуют точечно-
векторное аффинное пространство (от лат. a nis — смежный, соседний);
•на втором этапе в аффинном пространстве с помощью скалярного произведения вводятся метрические понятия рас-
стояний и углов, в результате получается евклидово пространство En.
Точки и векторы |
Пусть имеется |
арифметическое векторное |
|||||
в аффинном |
пространство Rn. Рассмотрим непустое мно- |
||||||
жество An элементов, которые мы бу- |
|||||||
пространстве |
|||||||
дем |
называть |
точками, |
причем каждой |
||||
|
|||||||
у п о р я д о ч е н н о й |
паре точек A, B An ставится в соот- |
||||||
|
|
X = AB |
|
Rn |
. Таким образом |
||
ветствие единственный вектор −→ |
−−→ |
|
|||||
вектор получает геометрическую интерпретацию и ему приписы-
вается направление от точки A к точке B. Заметим сразу, что об-
−→
ратное не верно, один и тот же вектор X может соответствовать
различным парам точек, то есть векторы являются свободными. Предположим выполнение следующих аксиом:
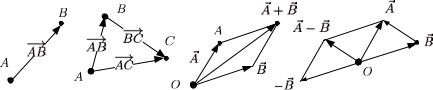
• откладывание вектора от точки (см. рис. 9.1, a). Для
−→
каждой точки A и каждого вектора X Rn найдется од-
−−→ −→
на и только одна точка B, что AB = X . Другими словами,
определена «межвидовая» операция сложения точки с век-
−→
тором, дающая в результате точку B = A + X ;
•сложение векторов по правилу треугольника (см. рис. 9.1, б ). Для любых трех точек A, B, C
−−→ −−→ −→
AB + BC = AC.
16 |
Глава 9. Теория выпуклого программирования |
Тогда все точки и все векторы образуют точечно-векторное (аффинное) пространство.
Точки и векторы аффинного пространства можно однозначно сопоставить друг другу. Для этого зафиксируем произвольную точку O — начало координат. Тогда по первой аксио-
ме любой точке A будет однозначно соответствовать вектор
−→
OA = (a1, . . . , an)T , отложенный в данную точку из начала координатп и называемый радиусом-вектором. Набор чисел a1, . . . , an задает координаты точки A в аффинной системе координат.
а) б) в) г)
Рис. 9.1. Точки и векторы в аффинном пространстве
Если предполагать начало координат заданным и считать по |
|
умолчанию векторы отложенными от точки O, т. е. сокращенно |
|
писать →− |
вместо −−→, то правило сложения векторов треуголь- |
X |
OX |
ником может быть заменено эквивалентным «правилом параллелограмма» (см. рис. 9.1, в), а вычитание векторов может быть интерпретировано как сложение с противоположным вектором
A |
B = A + ( B ) |
(см. рис. 9.1, г). При этом из аксиомы сложе- |
||||||
→− |
− →− →− |
−→− |
||||||
ния векторов следует, что −−→ |
−−→ |
− −→ |
→− |
− →− . |
||||
|
|
|
|
AB |
= OB |
OA |
= B |
A |
|
C другой стороны, каждому вектору →− |
будет соответствовать |
||||||
|
|
|
|
|
|
X |
|
|
точка X = O + →− . Поэтому межвидовую операцию сложения точ- |
||||||||
|
|
|
X |
|
|
|
|
|
ки A с вектором X можно заменить обычным векторным сложе- |
||||||||
нием −→ |
→− |
→− →− . |
|
|
|
|
||
|
OA |
+ X |
= A + X |
|
|
|
|
|
Итак, в аффинном пространстве можно оперировать двумя видами объектов: точками и векторами. Из точек можно строить разнообразные множества (геометрические места) и называть их фигурами. Например, прямая линия, проходящая через точку A в
9.1.. Евклидово пространство |
|
17 |
|
|||
направлении, заданном вектором |
→− |
, — это геометрическое место |
||||
точек X = A + t→− |
−∞ |
|
∞. |
d |
|
|
t |
|
|
|
|||
d , |
|
|
|
|
|
|
Если интерпретировать точки как концы соответствующих
радиусов-векторов при зафиксированном начале координат, то м о ж н о д л я т о ч е к и в е к т о р о в и с п о л ь з о - в а т ь о д и н а к о в о е «с т р е л о ч н о е» о б о з н а ч е- н и е, из контества всегда будет ясно, о чем идет речь. В частности, уравнение прямой можно записать в эквивалентном, чисто
−→ −→ −→
векторном виде X = A + t d , именно такую форму записи мы будем использовать в дальнейшем.
Вводить метрические понятия в аффинном пространстве можно различным образом, однако самым эффективным способом задания возможности измерений является аксиоматическое введе-
ние скалярного произведения векторов.
Определение. Аффинное пространство является евклидо-
→− →−
вым, если каждой паре векторов X , Y поставлено в соответ-
→− →−
ствие вещественное число X , Y , называемое их скалярным произведением, причем выполнены следующие аксиомы:
1) коммутативность:
|
|
|
→− →− |
= |
→− →− |
; |
|
|
|
||||
|
|
|
|
X , Y |
Y , X |
|
|
|
|||||
2) |
ассоциативность относительно умножения на веще- |
||||||||||||
ственное число α: |
|
|
−→ →− |
|
→− →− |
|
|
|
|||||
|
|
|
|
= |
; |
|
|
||||||
|
|
|
αX , Y |
α X , Y |
|
|
|
||||||
3) |
дистрибутивность относительно сложения векторов: |
||||||||||||
|
→− →− →− |
= |
→− →− |
|
+ |
→− →− |
|
; |
|||||
|
X |
+ Y , Z |
X , Z |
|
Y , Z |
|
|||||||
4) |
положительность скалярного квадрата: |
|
|
||||||||||
|
→− →− |
|
0 |
при |
→− |
→− |
|
→− →− |
= 0. |
||||
|
X , X |
|
|
X |
=0 , |
|
|
0 , 0 |
|||||

18 Глава 9. Теория выпуклого программирования
Для n-мерного арифметического пространства Rn, элементами которого являются столбцы вещественных чисел, понимаемые как матрицы размера n × 1, скалярное произведение векторов
X = (x |
, . . . , x )T |
Y = (y |
, . . . , y )T |
определяется путем мат- |
|||
→− |
1 |
n |
и →− |
1 |
n |
|
|
ричного умножения строки на столбец: |
|||||||
|
|
|
→− →− →− →− |
|
n |
||
|
|
|
|
i i |
|||
|
|
|
X , Y = X T Y = |
i |
|||
|
|
|
|
x y . |
|||
|
|
|
|
|
|
|
=1 |
Легко убедиться, что все аксиомы скалярного произведения при этом выполняются.
Измерение длин и углов
и расстояния.
Основываясь на базовом определении скалярного произведения, в евклидовом пространстве вводятся фундаментальные понятия длины (нормы)
Определение. Длиной (нормой, модулем) вектора в евклидовом пространстве называется корень квадратный из его скалярного квадрата1:
|
→− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
→− →− |
|
|
|
−→ −→ |
i |
|||||
|
|
|
|
|
|
|
i=1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
X = |
|
X , X = |
X T X = |
|
x2. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−→
Если вектор X умножить на масштабный коэффициент, обратный норме, то длина его станет равна единице. Такая операция называется нормированием:
→− →−X = →−X .
X
1Иногда определяющим понятием евклидова пространства считается не скалярное произведение, а определенная таким образом норма.
9.1.. Евклидово пространство |
19 |
Пользуясь понятием нормы, легко определить расстояние между точками X(x1, . . . , xn) и Y (y1, . . . , yn) в евклидовом пространстве:
ρ(X, Y ) = |
|
−−→ |
|
|
|
|
|
|
|
|
|
|
|
|
i |
− |
i |
||||
|
|
|
i=1 |
|
|
|
||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
XY |
|
= |
|
(x |
|
y )2. |
||
|
|
|
|
|
|
|
|
|
|
|
С введением расстояния пространство становится метрическим, возможно определение характерных для любого метрического пространства понятий окрестности, сходимости, замкнутости, ограниченности и ряда других, основанных на измерении расстояний.
Принципиальной особенностью евклидова пространства, выделяющей его из общего класса метрических пространств, является возможность измерения не только расстояний, но и углов.
→−
Определение. Угол ϕ между (ненулевыми) векторами X
→−
и Y в евклидовом пространстве определяется равенством
cos ϕ = |
→− →− . |
|||
|
X , Y |
|
|
|
|
→− |
· →− |
|
|
|
X |
Y |
|
|
Векторы, скалярное произведение которых равно нулю (угол между векторами равен ±π/2), называются ортогональными. Ортогональность обобщает на многомерный случай понятия перпендикулярности, рассматриваемые в двумерном и трехмерном пространствах. Понятие ортогональности можно распространить на множества: два множества векторов являются ортогональными, если каждый вектор первого ортогонален каждому вектору второго.
Векторы, угол между которыми равен 0 или π, называются |
|||
коллинеарными. Очевидно, векторы →− |
и →− коллинеарны тогда и |
||
X |
Y |
|
= 0 |
|
X = λY , λ |
||
только тогда, когда они пропорциональны, т. е. →− |
→− |
. |
|
