Методы оптимизации и исследование операций для бакалавров информатики. Часть 2

Scalar f "цена перевозки 1 шт. на расстояние квартала" /1/;

Parameter c(i,j) "матрица стоимости перевозок, у.е. за 1 шт."; c(i,j) = f*d(i,j) ;

Variables

x(i,j) "величина перевозки, шт." L "транспортные расходы, у.е.";

Positive variable x ;

В данном примере слова на русском языке в кавычках являются комментариями, они без изменений копируются в результаты. Однако на практике их лучше избегать либо пользоваться латиницей, так как некоторые компиляторы не воспринимают кириллицу. Индексы записываются в круглых скобках, для задания множества используются не фигурные скобки {a, b, c}, а две наклонные черты /a, b, c/, так как авторы языка посчитали, что не на всех клавиатурах есть соответствующие символы. Сочетание знаков «=e=» означает отношение равенства (equal), в отличие от оператора присваивания «=».

Оператор Sets объявляет множества индексов и присваивает их элементам содержательные текстовые значения, в нашем случае складам (Store_1, Store_2) и магазинам (Shop_1, Shop_2, Shop_3). Параметры (данные) модели объявляются и получают

значения с помощью операторов Scalar (единственное значение), Parameter(s) (список значений) и Table (таблица), для объявления переменных модели служит оператор Variables. Уравнения модели задаются оператором Equations, в нашем примере они линейные.

Описав модель задачи, можно вызвать необходимый решатель (в нашем случае решатель линейных задач lp), для этого достаточно написать предложение Solve transport using lp minimizing L.

Язык GAMS обладает достаточно мощными изобразительными возможностями, он позволяет описывать широкий класс линейных и нелинейных, в том числе дискретных, моделей и достаточно широко используется на практике3. Однако в нем нет четкого разделения программы на описание модели и задание данных, что является серьезным недостатком.

Язык AMPL (A Mathematical Programming Language) был разработан в 1990-х годах в Bell Laboratories для того, чтобы описывать и решать сложные задачи

оптимизации и теории расписаний. По назначению и структуре очень близок к GAMS, но он создавался позже, его синтаксис ближе к стандартному языку математики, что позволяет дать очень краткое и легкочитаемое определение задач математического программирования. Еще одним отличием AMPL является то, что описание модели в нем полностью отделено от ввода данных, это придает программе логическую стройность и гибкость4.

3Самая свежая документация по языку и системе, учебный курс, а также дистрибутивы для различных аппаратно-программных платформ доступны на сайте GAMS Development Corporation по адресу http://www.gams.com. Без лицензии программы работают в демо-режиме, ограничивающем число переменных и ограничений.

4Полная информация о языке AMPL, условия лицензирования, пробная и студенческая версии программ доступны на фирменном сайте http://www.ampl.com/.

П р и м е р. Переведем задачу из предыдущего примера на язык AMPL. Названия и назначения операторов почти полностью соответствуют GAMS и понятны без дополнительных пояснений, ключевое слово subject to хорошо знакомо математикам, оно переводится при условии. Объявления модели и присваивания данных разнесены, они даже могут находиться в разных файлах. Комментарии на русском языке оставлены для сопоставления с программой на языке GAMS, однако при практическом использовании языка комментарии следует писать на латинице.

##### МОДЕЛЬ #####

###Множества индексов ###

set Stores "склады" ; set Shops "магазины";

###Параметры ###

param a "запас на складе i, шт." {i in Stores}; param b "потребности магазина j, шт." {j in Shops};

param d "расстояние в кварталах" {i in Stores, j in Shops}; param c "матрица стоимости перевозок, у.е. за 1 шт."

{i in Stores, j in Shops} = f * d[i,j];

param f "цена перевозки 1 шт. на расстояние квартала";

### Переменные ###

var x "план перевозок" {Stores,Shops}>=0;

### Целевая функция ###

minimize L: sum {i in Stores, j in Shops} c[i,j] * x[i,j];

### Ограничения ###

subject to {i in Stores}: sum {j in Shops} x[i,j] = a[i]; subject to {j in Shops}: sum {i in Stores} x[i,j] = b[j];

##### ДАННЫЕ #####

data;

set Stores := Store_1 Store_2; set Shops := Shop_1 Shop_2 Shop_3;

param f := 1; end;

Так же как и в системе GAMS, компилятор AMPL не решает задачу сам, а передает ее внешнему решателю. Если запустить приведенную выше модель на фирменном сервере AMPL, попросив подключить широко известный решатель MINOS, будет выдан следующий результат.

Доступ к сетевым серверам, обеспечивающим рабоСетевые ту решателей, возможен с различных сайтов, как решатели коммерческих, так и свободных. В частности, упомянутые выше фирменные сайты GAMS и AMPL предоставляют право бесплатно решать задачи небольшого раз-

мера в демонстрационном режиме.

Глава 14

Динамическое

программирование

В отличие от всех предыдущих методов оптимизации, динамическое программирование, созданное выдающимся американским математиком Ричардом Беллманом (см. исторические замечания в конце главы), не описывается конкретным алгоритмом, его правильнее рассматривать как специфический подход к решению задач определенного класса — многошаговых процедур принятия решений.

Излагать этот раздел исследования операций можно поразному. Некоторые авторы идут от общего к частному, формулируя общую проблему многошаговой оптимизации в пространстве состояний и конкретизируя ее в конкретных ситуациях. Мы поступим по-другому: на нескольких элементарных примерах попытаемся продемонстрировать основные принципы динамического программирования. Внешне они очень просты, однако эта простота обманчива, так как за кажущейся очевидностью скрыт глубокий смысл.

14.1. Задача о кратчайшем пути

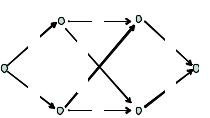
П р и м е р. Шесть населенных пунктов, обозначенных буквами a, b, c, d, e, f, связаны сетью дорог, представленных графом на рис. 14.1. Цифры показывают расстояние между соседними пунктами (вершинами графа), движение одностороннее. Требуется найти кратчайший путь из a в f .

bd

4

сe

Рис. 14.1. Пример задачи о кратчайшем пути

Поставленная задача определенно вызовет снисходительную улыбку у читателя, даже не знакомого с теорией графов. Здесь имеется всего четыре варианта, их легко перебрать и

получить кратчайший путь a → c → e → f . Но не торопитесь с выводами. На этом примитивном примере мы рассмотрим фундаментальные идеи динамического программирования и сделаем далеко идущие обобщения.

Базовых принципов динамического программирования три:

•принцип многошаговости,

•принцип погружения,

•принцип оптимальности.

Принцип многошаговости состоит в том, что исходная многомерная задача развертывается во времени и представляется как целенаправленный многошаговый процесс движения в пространстве состояний (отсюда название динамического программирования), причем на каждом шаге решается простейшая одномерная задача.

bd

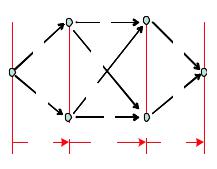
Рис. 14.2. Превращение задачи в многошаговую

В нашем примере превращение переборной задачи в многошаговую происходит естественным образом. Состояния соответствуют вершинам графа. Если образовать четыре условных рубежа, показанных на рис. 14.2, то шагом можно считать перемещение в соседнюю вершину следующего рубежа. Таким образом, наша задача теперь заключается в том, чтобы за три шага дойти из вершины a до цели, причем на каждом шаге принимается простейшее решение — свернуть налево или направо. По причине, которая станет ясной в следующем абзаце, нумерацию рубежей индексом k удобно вести с конца, от цели пути.

Принцип погружения состоит в том, что исходная задача с конкретным числом шагов n и конкретным начальным состоянием погружается в класс задач с числом шагов k = 0, 1, . . . , n и всевозможными допустимыми начальными состояниями.

Этот принцип способен вызвать недоумение: какой смысл со-

знательно усложнять поставленную задачу? Однако в нем заключается вся хитрость подхода, предложенного Беллманом. Весь класс задач будет решаться рекуррентно, с конца, то есть с k = 0, при этом при увеличении k будут использоваться результаты предыдущего решения.

В нашем случае число шагов k меняется от 0 до 3, и весь класс задач выглядит следующим образом.

•k = 0: за 0 шагов дойти до цели из вершины f (тривиальная задача);

•k = 1: за 1 шаг дойти кратчайшим путем до цели из вершин d или e;

•k = 2: за 2 шага дойти кратчайшим путем до цели из вершин b или c;

•k = 3: за 3 шага дойти кратчайшим путем до цели из вершины a.

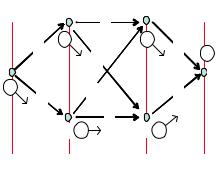
Приступаем к решению сформулированного класса задач. Ход решения будем фиксировать, устанавливая около каждой рассмотренной вершины графа пометку — указатель в виде кружка с числом и стрелкой, где число обозначает длину к р а т ч а й ш е г о пути до цели из этой вершины, а стрелка указывает оптимальное решение в данном месте, то есть направление, соответствующее кратчайшему пути. На местности указатель можно представить себе в виде закопанного у развилки дорог столбика с соответствующей надписью.

Начнем с k = 0, то есть с конца. Задача состоит в том, чтобы за ноль шагов дойти из пункта f до цели. Ответ тривиален: никуда идти не нужно, при этом длина кратчайшего пути равна нулю. Ставим соответствующий указатель около вершины f (см. рис. 14.3).

Переходим к k = 1. Возможными начальными состояниями для одношаговой задачи являются вершины первого с конца рубежа, то есть вершины d и e. Для них решение также очевидно:

bd

Рис. 14.3. Расстановка пометок у вершин

вариантов пути нет. Ставим соответствующие пометки у данных вершин.

Увеличиваем k до 2 и рассматриваем подкласс двухшаговых задач. Возможными начальными состояниями в этом случае являются вершины второго с конца рубежа: b и c. Здесь уже возможны варианты, выбрать оптимальное решение поможет третий фундаментальный принцип динамического программирования.

Принцип оптимальности. Оптимальное поведение обладает тем свойством, что каковы бы ни были начальное состояние и начальное решение, последующее поведение должно быть оптимальным о т н о с и т е л ь н о с о с т о я н и я, п о л у - ч и в ш е г о с я в р е з у л ь т а т е н а ч а л ь н о г о р е ш е н и я.

Эту формулировку, данную самим Беллманом, невозможно улучшить, в ней важно каждое слово, поэтому ее следует не просто понять, а выучить наизусть.

Сделаем подробный разбор принципа оптимальности применительно к нашей задаче. Поведение означает последовательность решений, приводящих систему из некоторого начального в заданное конечное — целевое — состояние. Соответственно оптимальное поведение есть последовательность оптимальных решений.