Примеры видов линий.

1.Простейшая линия

• прямая;

• отрезок;

• луч;

• окружность (в силу математического определения линии);

2.Элементарная линия

• полуокружность с концами : она гомеоморфна отрезку;

• синусоида 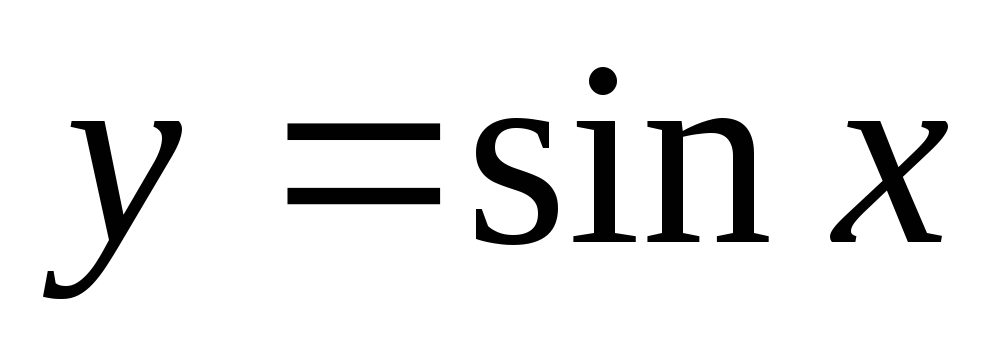, заданная в системе координат 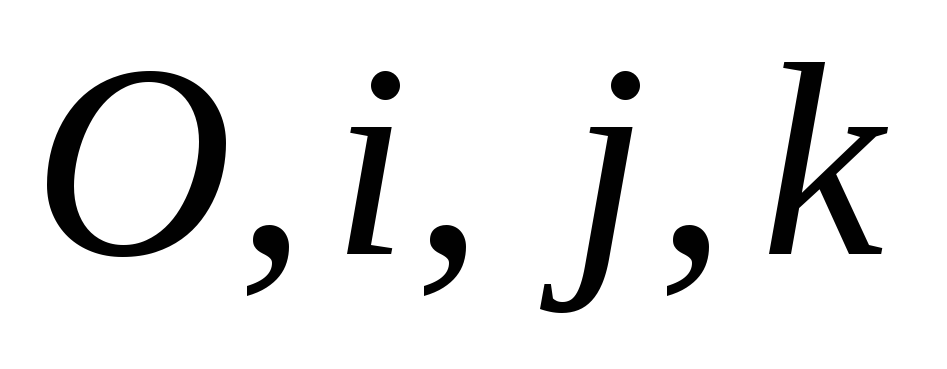уравнениями: 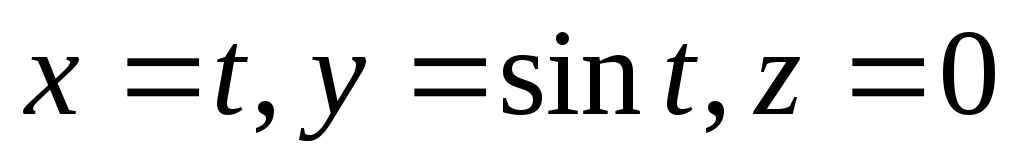, где 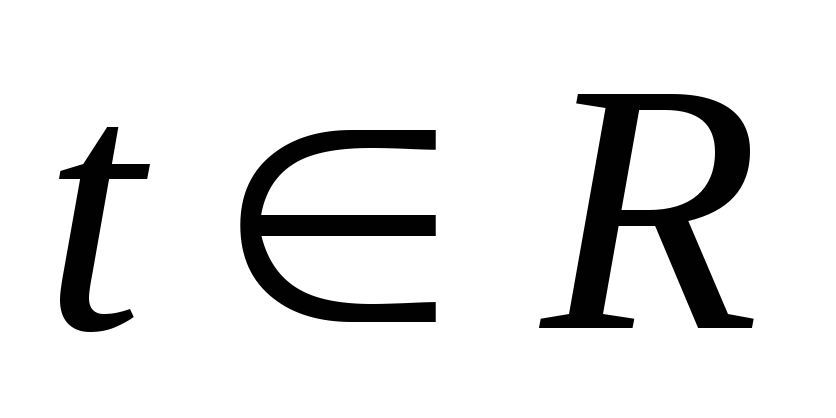. Эти уравнения устанавливают гомеоморфизм между множеством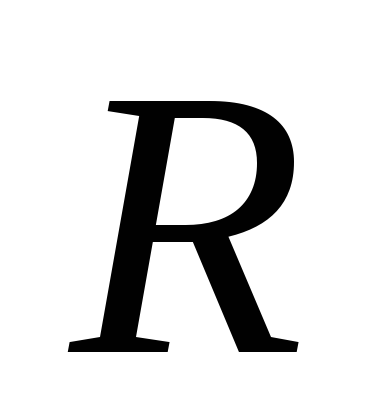 и синусоидой.

3. Гладкие линии

• Уравнения ,

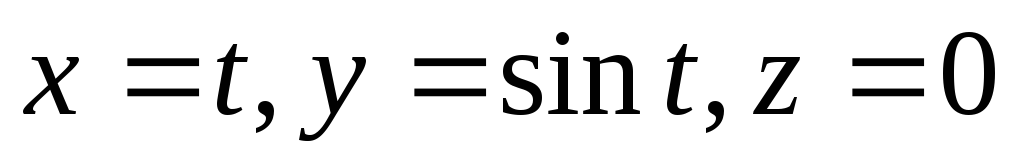Определяют синусоиду на плоскости . Правые части уравнений синусоиды имеют в непрерывные производные любого порядка: и условие (2) выполнено => синусоида – гладкая линия класса;

4.Кусочно-гладкие линии.

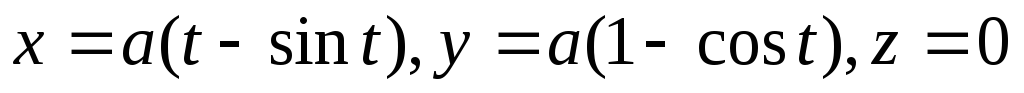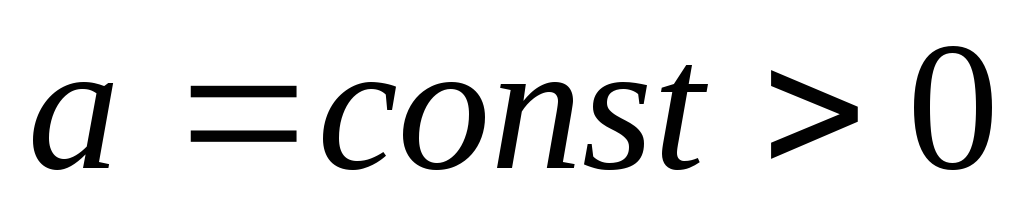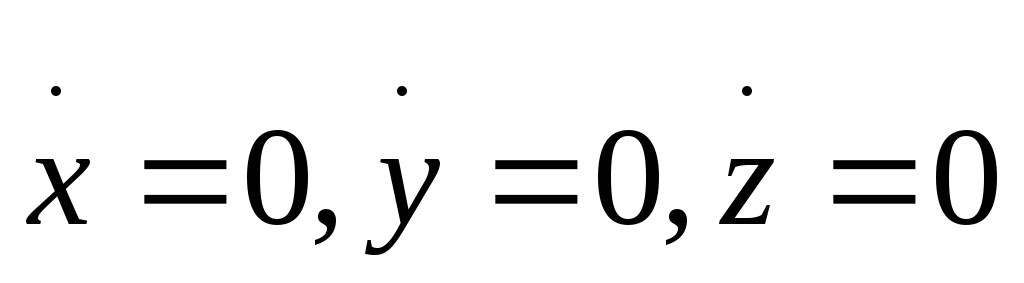
• Циклоида, определяемая уравнениями , где . Но она не является гладкой т.к. Ранг 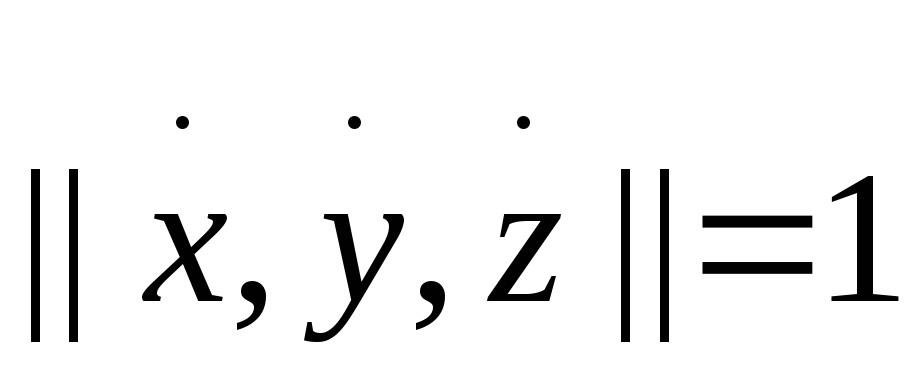(2) нарушено.

Y

x

Касательная.

Теорема 1.29 В каждой точке гладкой линии заданной уравнением ,существует касательная прямая, которая определяется вектором .

Доказательство:

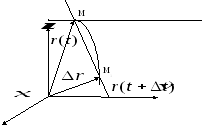
1). Вектором - направляющий вектор секущей .

2). Устремим к нулю. , тогда секущая прямой - направляющий вектор касательной.

3). Рассмотрим другую параметризацию данной кривой , получаем по условию гладкости. То - направляющий вектор касательной.

Параметризация кривой.

Кривая и числовой промежуток

Зададим

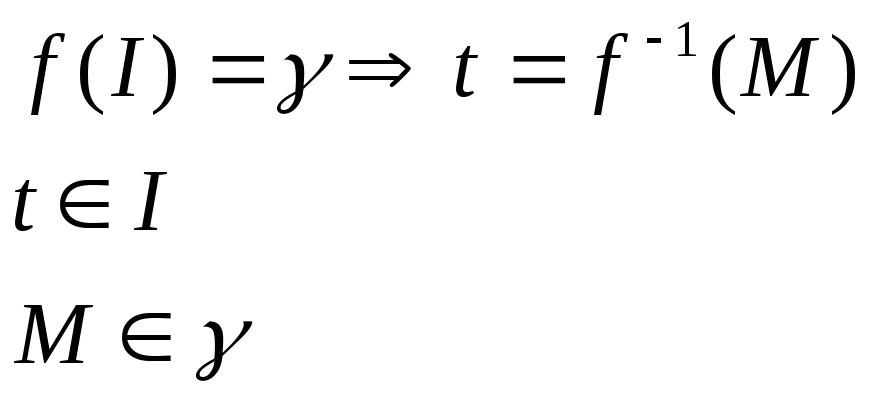
Определение 1.30 Гомеоморфизм (тот или иной)- называется параметризацией кривой, так как он порождает эту линию.

Так как одну и туже линию можно задать различными гомеоморфизмами, то значит, что одна и та же линия задается различной параметризацией.

Схема изменения параметра линии.

- Вводится числовой промежуток

- Задается не который гомеоморфизм h переводящий в ,

- Через новый

- В уравнении линии подставляется полученное выражение

Если кривая гладкая, то функция должна быть дифференцируема в промежутке ; должна иметь первую производную отличную от нуля; линия при новой параметризации должна принадлежать к тому же классу что и при старой параметризации (иметь непрерывные производные до порядка включительно старой параметризации) водную отличную от нуля; линия при новой параметризации должна принадлежать к тому же классу, что и пр).