
Лекция №2
Касательная к линии. Естественная параметризация и длина дуги.
Рассмотрим некоторую линию в прямоугольной системе координат в Е3.
![]() -гладкая
линия класса Ск.
-гладкая
линия класса Ск.

rang (x(t),y(t),z(t))=1
M![]()
![]() 0 M1
0 M1
![]() 0
0
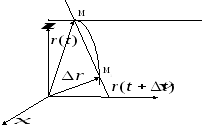
MM1=r(t+∆t)-
r(t)![]()
Терема:2.1.
Каждой точки М гладкой линии класса Ск
заданной
векторным уравнениям существует
касательная, которая определяется т.М
и направляющим вектором
![]() .
.
Доказательство:
1). Вектором
![]() -
направляющий вектор секущей ММ1.
-
направляющий вектор секущей ММ1.
2). Устремим ∆t
к нулю.
![]() секущая
секущая
![]() прямой
прямой
![]() -направляющий
вектор касательной.
-направляющий
вектор касательной.
3). Рассмотрим
другую параметризацию данной кривой
![]() ,получаем
,получаем
![]() по условию гладкости .
по условию гладкости .
То
![]()
Естественная параметризация кривой
Определение:2.2.
Параметризация S
регулярной линии, называется естественной,
если векторная функция R=R(S),
заданная на промежутке I0
и определяющая кривую в этой параметризации
обладает свойством
![]()
Покажем что для
всякой регулярной кривой существует
естественная параметризация . Пусть S
естественная параметризация линии L,
тогда существует некоторая функция
s=s(t)
выражающая естественный параметр через
произвольный параметр
![]() s’=s’(t)
s’=s’(t)![]() 0,
по определению допустимой замены
параметра. Будем считать что
s’(t)>0
0,
по определению допустимой замены
параметра. Будем считать что
s’(t)>0![]() существует
функция ей обратная t=t-1(s)
–строго возрастающая. По естественному
параметру l:R=R(S)
по произвольному параметру l1
: r=r(t).
Если в записи кривой L
в уравнение включить оба параметра
R(S)=r(t(S))-получили
следующую функцию.
существует
функция ей обратная t=t-1(s)
–строго возрастающая. По естественному
параметру l:R=R(S)
по произвольному параметру l1
: r=r(t).
Если в записи кривой L
в уравнение включить оба параметра
R(S)=r(t(S))-получили
следующую функцию.
![]() т.к S
естественный параметр
т.к S
естественный параметр
![]()
![]()
![]()

![]() .
Из I0
.
Из I0![]() I
I
Т.к функция s=s(t)
является допустимой заменой параметра,
то s’(t)
>0 из
![]() =
=
![]() значит всегда существует допустимые
изменения параметра осуществляющие
переход от произвольной параметризации
к естественной.
значит всегда существует допустимые
изменения параметра осуществляющие
переход от произвольной параметризации
к естественной.
![]() переход
от t
к S.
переход
от t
к S.
Длина дуги является
геометрическим обоснованием естественной
параметризации. Определитель
![]()
![]() =1
– условие естественной параметризации.
=1
– условие естественной параметризации.
Вектор
![]() является
направляющим вектором касательной к
линии в соответствующей т.М, называется
единичным вектором касательной к линии
и обозначается
является
направляющим вектором касательной к
линии в соответствующей т.М, называется
единичным вектором касательной к линии
и обозначается
![]() .
.
Если даны для линии
две естественные параметризации S
и S*
то они
связанные соотношением S*=![]()
![]() и
и
![]() .
.
Кривизна и кручение линии в естественной параметризации.

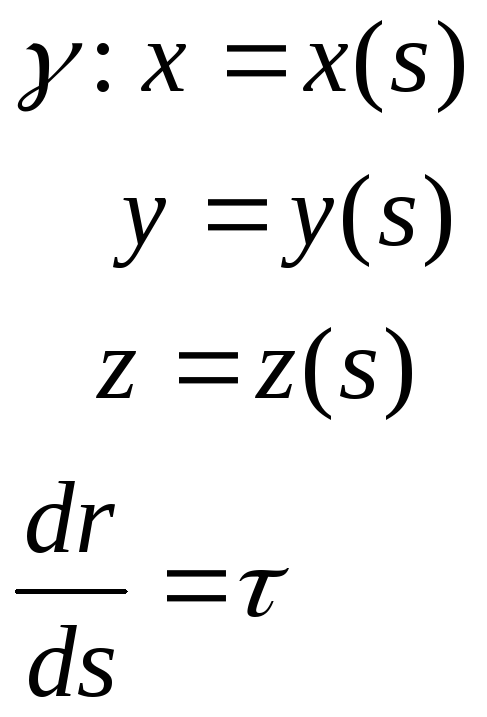
Определение 2.3
Вектор
![]() называется
вектором кривизны.Его длина обозначается
называется
вектором кривизны.Его длина обозначается
![]() и
называется кривизной линии
и
называется кривизной линии
![]() в точке М. На всей линии
в точке М. На всей линии
![]() кривизна
кривизна
![]() является
функцией параметра S.
является
функцией параметра S.
Определение 2.4.
Число
![]()
![]() ,
где
,
где
![]()
![]() 0
называется радиусом кривизны в данной
точке
0
называется радиусом кривизны в данной
точке
![]() (по
лемме 1.12)
(по
лемме 1.12)![]()
![]()
![]()
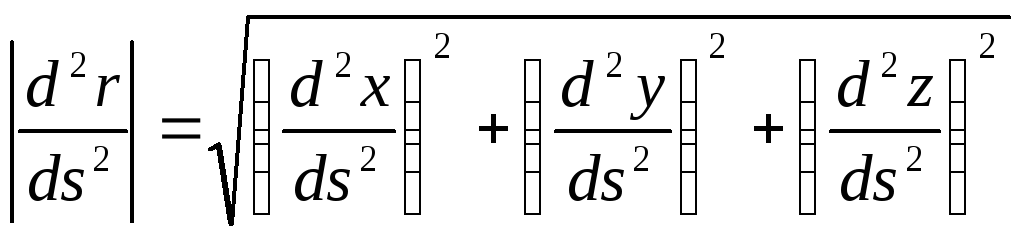
Теорема 2.5. Для того чтобы связанная линия была простейшей, необходимо и достаточно чтобы кривизна была равна нулю в каждой точки линии.
Связной линией называется линия, состоящая из точек распределения, т.е r’(s)║ r’’(s).
Доказательство:
1). Пусть
![]() -
простейшая (прямая), тогда
-
простейшая (прямая), тогда
![]() :
:
![]() 0
,где
0
,где
![]()
p
и r0
–постоянные
векторы
![]() точки.
точки.
2). Пусть кривизна
равна нулю, для любой точки из формулы
кривизны![]()
Параметрическое задание прямой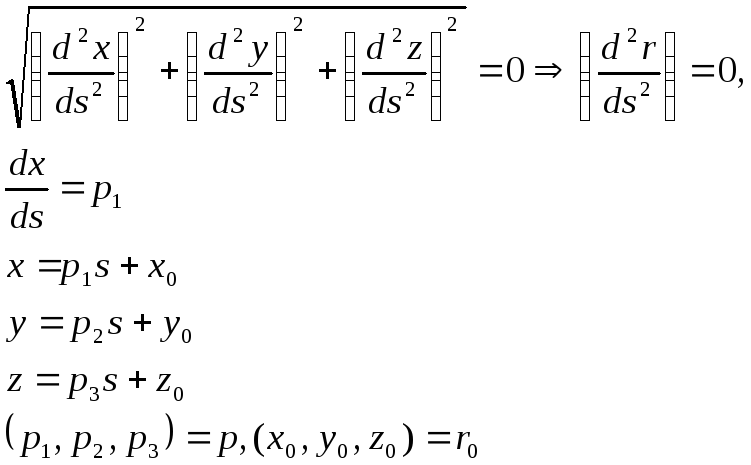
Определение 2.6.
Прямая проходящая через т.М ║![]() (M,N)
называется главной нормалью линии
(M,N)
называется главной нормалью линии
![]() т.М.
т.М.
![]()
![]() главная
нормаль
главная
нормаль
![]() касательной.
касательной.
Определение 2.7.
Вектор равный отношению
![]() называется единичным вектором главной
нормали
называется единичным вектором главной
нормали
![]()
Определение2.8.
Прямая проходящая через т.М и вектор
![]() называется бинормалью линии
называется бинормалью линии
![]() в точке М.
в точке М.
![]() -единичный
вектор бинормаль
-единичный
вектор бинормаль
По определению
векторное произведение
![]()
![]()
Определение
2.9.. Четверка
состоящая из т.М, векторов
![]() определяет прямоугольную систему
координат (ортонормированный репер) и
обозначается Rn
называемый
каноническим репером линии
определяет прямоугольную систему
координат (ортонормированный репер) и
обозначается Rn
называемый
каноническим репером линии
![]() в т.М.
в т.М.
Определение
2.10. Плоскости,
обратные: т.М,![]() -
соприкасающая плоскость, т.М, n,
-
соприкасающая плоскость, т.М, n,![]() -нормальная
плоскость т.М,
-нормальная
плоскость т.М,![]() -спрямляющая
плоскость.
-спрямляющая
плоскость.
Т.к точка М подвижна то Rn тоже подвижен.
Соприкасающая плоскость является единственной плоскостью имеющая с кривой точку касания 2го порядка.
Определение
2.11. Фигура
образованная тремя прямыми (М,n),
(M,![]() ),(M,b)
и тремя плоскостями называется
сопровождающим трехгранником кривой
),(M,b)
и тремя плоскостями называется
сопровождающим трехгранником кривой
![]() .
.
Спрямляющая
плоскость (М,![]() )
делит пространство, на два полу
пространства. Одно из которых является
полупространством вогнутости. Вектор
n
однозначно определяется кривой
относительно естественного параметра,
а вектор
)
делит пространство, на два полу
пространства. Одно из которых является
полупространством вогнутости. Вектор
n
однозначно определяется кривой
относительно естественного параметра,
а вектор
![]() и
и
![]() могут иметь свои направления.
могут иметь свои направления.
