
Лекция 2.
Координаты точки на проективной прямой и проективной плоскости. Условие коллинеарности трех точек прямой. Уравнение прямой. Преобразование проективных координат.
Определение 2.1. Точками общего положения называется система к-точек, причем К≥3, если никакие три из них не лежат на одной прямой.
Определение 2.2. Проективным репером или проективной системой координат на проективной плоскости называется упорядоченная система точек Е1 , Е2 , Е3 , Е.
Точки Е1 , Е2 , Е3 , называют координатными точками, а Е – единичной точкой репера.
Определение 2.3. Реперами согласованности называются векторы, порожденные проективным репером.
Если
![]() выбраны так, что
выбраны так, что
![]() ,
то говорят, что система этих векторов
согласована относительно репера R.
,
то говорят, что система этих векторов
согласована относительно репера R.
Лемма 2.4.
Если каждая из систем векторов (![]() )
и (
)
и (![]() )
согласованы относительно данного репера
)
согласованы относительно данного репера
![]() ,
то существует такое число
,
то существует такое число
![]() ,
не равное нулю, что
,
не равное нулю, что
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
В проективном пространстве Рn проективный репер задаётся n+2 точками общего положения [Р1: R=(Е1, Е2, Е)].
Координаты на проективной плоскости
Пусть некоторый
вектор
![]() порождает в проективной плоскости
точку Х.
В системе координат
порождает в проективной плоскости
точку Х.
В системе координат
![]() вектор
вектор
![]() можно выразить через базисные векторы
можно выразить через базисные векторы
![]() .
.
Но так как векторы
![]() порождают проективную плоскость и
проективную систему координат, то числа
порождают проективную плоскость и
проективную систему координат, то числа
![]() называются
проективными координатами точки Х
в проективном репере.
называются
проективными координатами точки Х
в проективном репере.
Х не является нулевым вектором, поэтому все его координаты не равны нулю, а, значит, координаты точки Х одновременно не могут равняться нулю.
Определение 2.5.
Проективными
координатами точки на проективной
прямой (проективной плоскости) относительно
проективного репера
![]() называют координаты вектора, порождающего
данную точку, относительно базиса
векторного пространства, согласованного
с репером
называют координаты вектора, порождающего
данную точку, относительно базиса
векторного пространства, согласованного
с репером
![]() .
.
Свойства координат:
-
В проективном пространстве
 точка имеет к+1
координату;
точка имеет к+1
координату; -
Нет точки с нулевыми координатами;
-
Координаты – однородный набор чисел, поэтому они определяются с точностью до числового множителя;
-
Пропорциональные наборы определяют одну и ту же проективную точку.
Лемма 2.6.
Если однородный набор
![]() является координатами некоторой точки
Х
в репере R,
а система векторов (
является координатами некоторой точки
Х
в репере R,
а система векторов (![]() )
является согласованной относительно
этого репера, то вектор
)
является согласованной относительно
этого репера, то вектор
![]() также
порождает точку Х,
следовательно, Х=λУ
(они порождают одну и ту же точку).
также
порождает точку Х,
следовательно, Х=λУ
(они порождают одну и ту же точку).
Задача:
построить точку
![]() относительно
проективного репера
относительно
проективного репера
![]() .
.
Теорема 2.7. (о принадлежности трёх точек одной прямой)
Три проективные точки Х, У, Z, заданные своими координатами
 ,
,

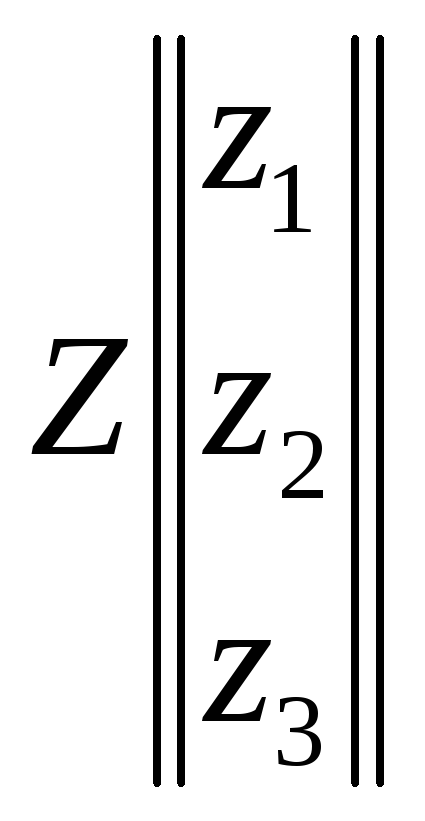 принадлежат одной прямой тогда и только
тогда, когда
принадлежат одной прямой тогда и только
тогда, когда
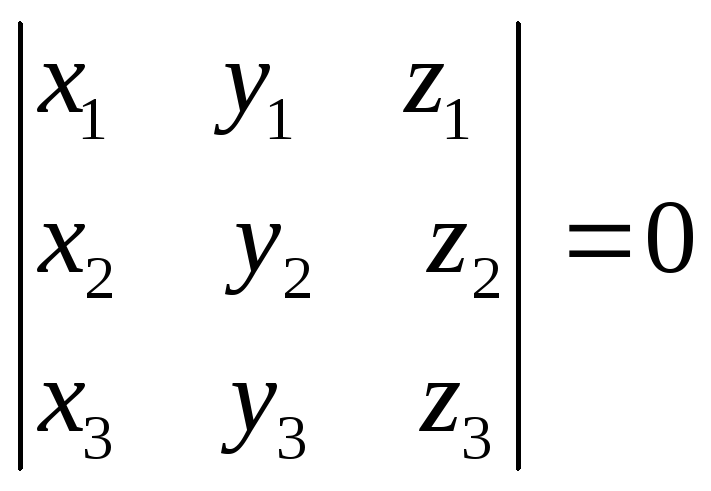

Доказательство
-
Пусть задан репер
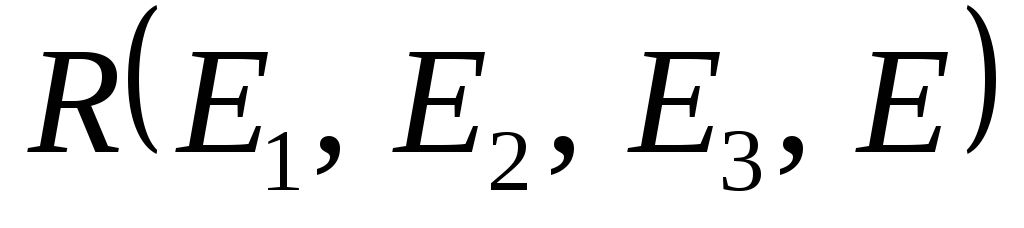 ,
его векторы
,
его векторы
 согласованы относительно R.
Отсюда следует, что вектор
согласованы относительно R.
Отсюда следует, что вектор
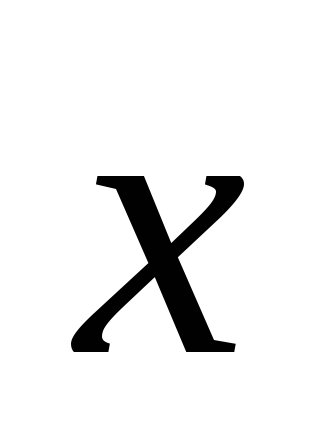 порождает точку Х,
порождает точку Х,
 -
У,
-
У,
 – Z;
– Z; -
Для того, чтобы точки Х, У, Z лежали на одной прямой необходимо, чтобы векторы
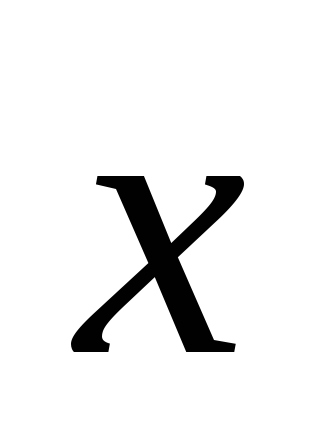 ,
,
 ,
,
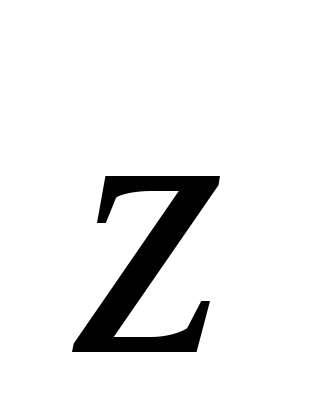 располагались в одной плоскости
аффинного пространства, т.е. они
компланарны, а, значит, определитель
располагались в одной плоскости
аффинного пространства, т.е. они
компланарны, а, значит, определитель
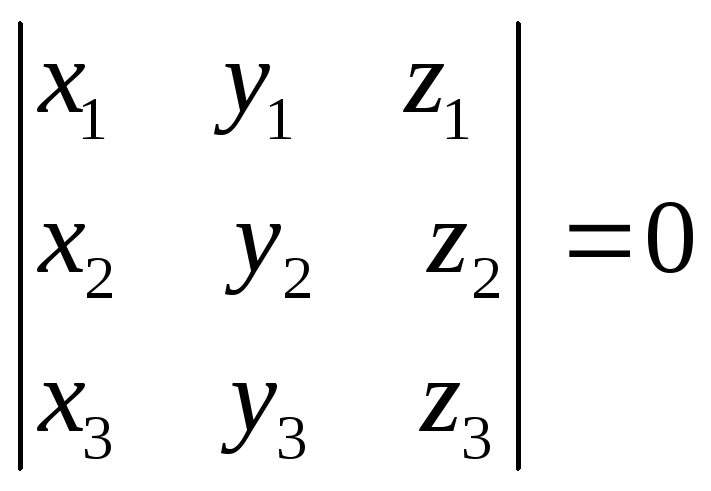
Проекция проективной точки на координатные прямые
П усть
задан репер R
= (A1,
A2,
A3,
E)
и Х
– произвольная точка проективного
пространства, Х3
= (A3X)
∩ (A1A2).
усть
задан репер R
= (A1,
A2,
A3,
E)
и Х
– произвольная точка проективного
пространства, Х3
= (A3X)
∩ (A1A2).
R1 = (A2, A3, Е1),
R2 = (A1, A3, Е2),
R3=(A1,A2,Е3) – проективные реперы.
Теорема 2.8. (о координатах проекции точки на координатную прямую)
Если произвольная точка Х (х1 : х2 : х3), не совпадающая с A3, в репере R спроецирована на прямую (A1A2), то в репере R3 её проекция Х3 будет иметь координаты (х1 : х2 ).
Доказательство
1. Т.к. точка Х3
принадлежит прямой (А1А2),
то в репере
![]() она имеет координаты (y1
: y2
: 0). Точки A3,
X3,
X
коллинеарны. Следовательно,
она имеет координаты (y1
: y2
: 0). Точки A3,
X3,
X
коллинеарны. Следовательно,

2. Т.к. точка Е3
принадлежит прямой (А1А2),
то в репере
![]() она имеет координаты (z1
: z2
: 0). Точки А3,
Е, Е3
коллинеарны. Следовательно,
она имеет координаты (z1
: z2
: 0). Точки А3,
Е, Е3
коллинеарны. Следовательно,
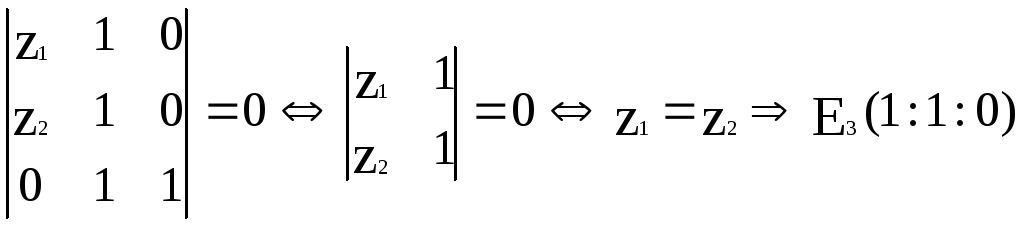
3. Пусть некоторая
согласованная система векторов
![]() порождает проективный репер R,
вектор
порождает проективный репер R,
вектор
![]() - точку Х3,
вектор
- точку Х3,
вектор
![]() - точку Е3.
Тогда имеем:
- точку Е3.
Тогда имеем:![]() (*),
(*),
![]() (**)
(**)
Из равенства (**)
следует, что система векторов
![]() согласована относительно репера R3.
Тогда из равенства (*) получаем, что
вектор
согласована относительно репера R3.
Тогда из равенства (*) получаем, что
вектор
![]() имеет координаты (х1,
х2).
Значит, точка Х3
имеет координаты (х1
: х2
) в репере R3.
имеет координаты (х1,
х2).
Значит, точка Х3
имеет координаты (х1
: х2
) в репере R3.
Однородные и неоднородные координат на расширенной прямой и расширенной плоскости
Рассмотрим на
расширенной прямой
![]() проективный
репер
проективный
репер
![]()
С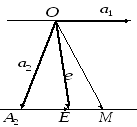 истема
векторов
истема
векторов
![]() согласована относительно данного
репера, т.е.
согласована относительно данного
репера, т.е.
![]()
М – произвольная
точка, имеющая координаты относительно
проективного репера
![]() .
.
На прямой
![]() рассмотрим
аффинный репер
рассмотрим
аффинный репер
![]() ,
порожденный проективным репером
,
порожденный проективным репером
![]() .
Пусть
.
Пусть
![]() - координата точки М в аффинном репере
- координата точки М в аффинном репере
![]() ,
т.е.
,
т.е.
![]() ,
,
![]() .
.
Следовательно,
точка М имеет координаты
![]() относительно репера
относительно репера
![]() .
Учитывая, введенные выше обозначения
для проективных координат точки М,
получили
.
Учитывая, введенные выше обозначения
для проективных координат точки М,
получили
![]() ,
,
![]() .
Отсюда
.
Отсюда
![]() и
и
![]()
Таким образом,
аффинные координаты собственной точки
М равны отношению проективных координат
этой точки в репере
![]() .
.
Проективные
координаты
![]() называют однородными координатами
точки М, аффинные
называют однородными координатами
точки М, аффинные
![]() - неоднородными координатами точки М.
- неоднородными координатами точки М.
Аналогичная связь
между аффинными координатами и
проективными координатами собственной
точки прослеживается и на расширенной
плоскости в репере
![]() :
:
![]() .
.
Уравнение прямой
Рассмотрим
проективный репер R
= (A1,
A2,
A3,
E)
на проективной плоскости. Прямая
![]() задана точками
задана точками
![]() и
и
![]() .
Точка
.
Точка
![]() -
произвольная точка прямой
-
произвольная точка прямой
![]() .
По теореме 2.7. имеем:
.
По теореме 2.7. имеем:
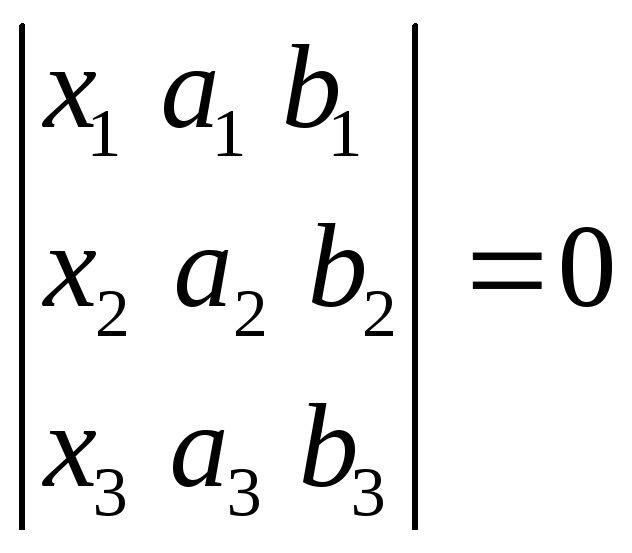 - уравнение прямой
проходящей через две точки.
- уравнение прямой
проходящей через две точки.
Разложив определитель
по элементам первого столбца, имеем:
![]() ,
где
,
где
![]() - соответствующие разложению определители
второго порядка.
- соответствующие разложению определители
второго порядка.
![]() - координаты прямой.
- координаты прямой.
Точки
![]() прямой
прямой
![]() порождены линейно зависимыми векторами
порождены линейно зависимыми векторами
![]() соответственно, а значит справедливы
равенства:
соответственно, а значит справедливы
равенства:
![]() - векторное уравнение
прямой;
- векторное уравнение
прямой;
 -
параметрические уравнения прямой.
-
параметрические уравнения прямой.
Преобразование проективных координат.
Рассмотрим
на проективной плоскости
![]() два проективных репера
два проективных репера
![]() и
и
![]() .
Точки
.
Точки
![]() порождаются системой согласованных
векторов
порождаются системой согласованных
векторов
![]() ,
т.е.
,
т.е.
![]() .
Известно положение нового репера
относительно старого, то есть известны
координаты новых координатных точек
.
Известно положение нового репера
относительно старого, то есть известны
координаты новых координатных точек
![]() и
и
![]() относительно репера
относительно репера
![]() ,
порожденных соответственно системой
векторов
,
порожденных соответственно системой
векторов
![]() :
:
|
|
|
|
|
|
|
|
|
Задача. Найти
связь между координатами точки М
относительно реперов
![]() и
и
![]()
1.
Выразим
векторы, репера
![]() через векторы репера
через векторы репера
![]() :
:
![]()
![]()
![]() (*)
(*)
![]()
2. Рассмотрим два случая.
1 случай.
Система векторов
![]() согласована относительно репера
согласована относительно репера
![]() ,
т.е.
,
т.е.
![]() .
(**)
.
(**)
-
Из (*) и (**) следует, что в этом случае выполняется совокупность равенств:
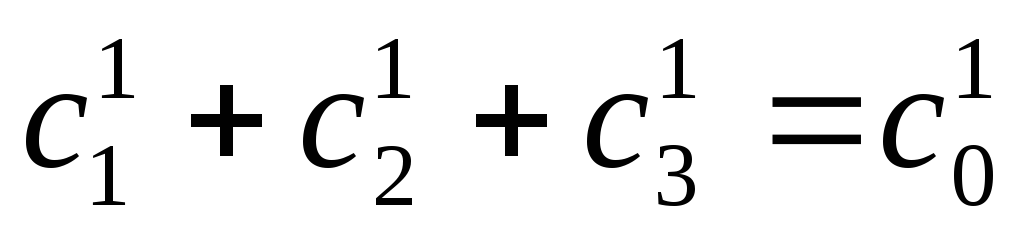 ,
,
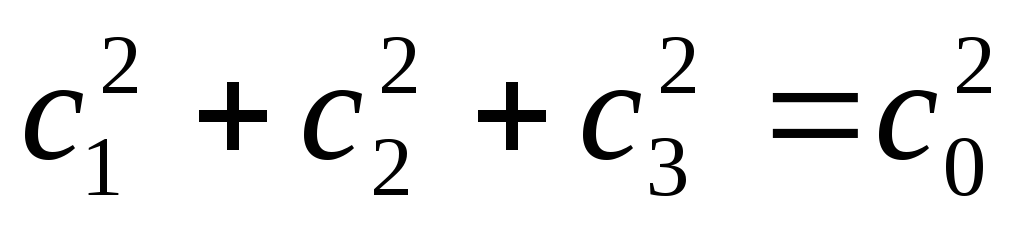 ,
,
 .
. -
Так как произвольная точка
 проективной
плоскости порождается различными
векторами
проективной
плоскости порождается различными
векторами
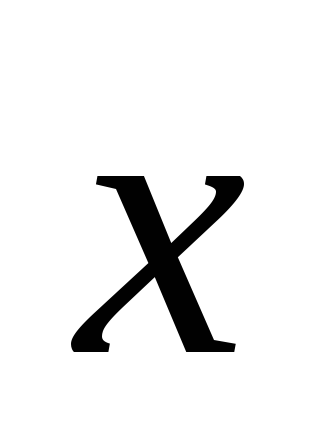 и
и
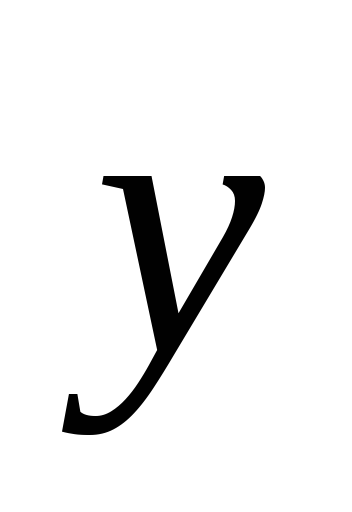 в реперах
в реперах
 и
и
 ,
то по лемме
2.6.
,
то по лемме
2.6.
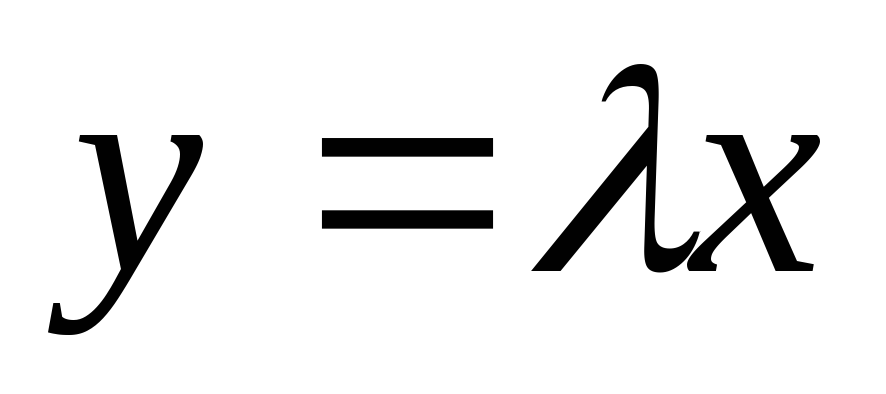 ,
где
,
где
 .
Разложим векторы
.
Разложим векторы
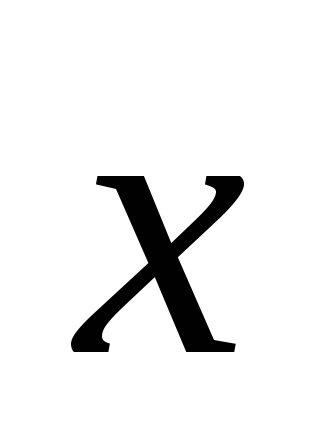 и
и
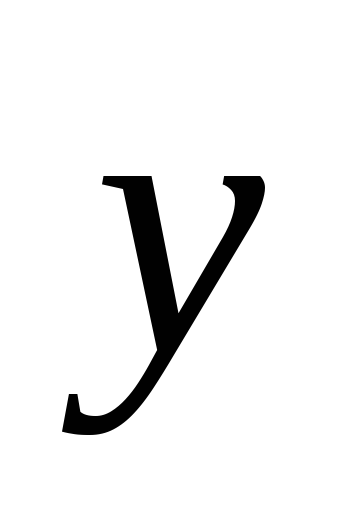 по векторам соответствующих базисов:
по векторам соответствующих базисов:
 .
Подставим вместо
.
Подставим вместо
 их
разложения из формул (*):
их
разложения из формул (*):
![]() (
(![]() )+
)+![]() (
(![]() )+
)+![]() (
(![]() )=
)=![]()
-
Так как векторы
 линейно независимы, то, приравнивая
коэффициенты при соответствующих
векторах в левой и правой частях
получившегося выражения, имеем искомые
формулы преобразования координат:
линейно независимы, то, приравнивая
коэффициенты при соответствующих
векторах в левой и правой частях
получившегося выражения, имеем искомые
формулы преобразования координат:

![]()
![]()
-
Матрица перехода от нового проективного репера к старому:
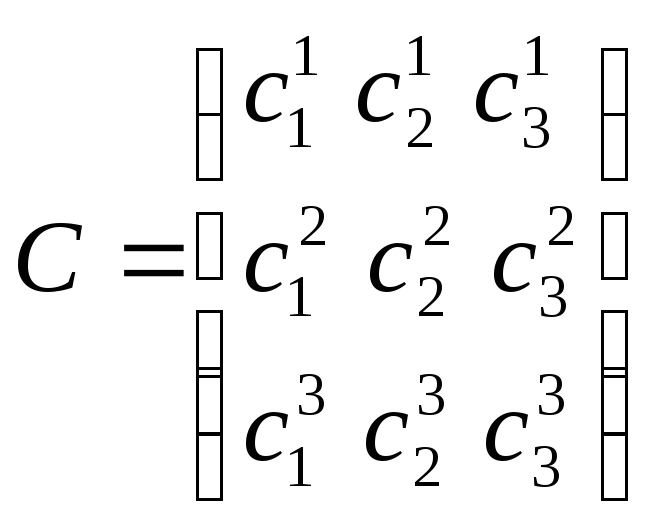 .
Определитель матрицы
.
Определитель матрицы
 отличен от нуля, так как точки
отличен от нуля, так как точки
 - неколлинеарные, векторы их порождающие
- неколлинеарные, векторы их порождающие
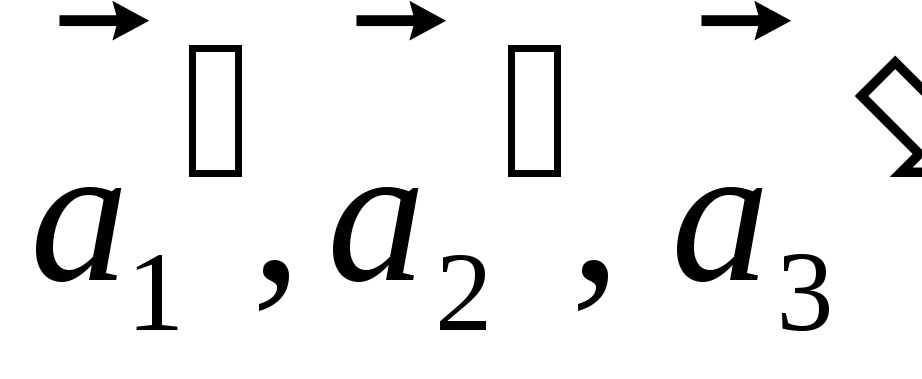 - линейно независимы.
- линейно независимы.
2 случай.
Система векторов
![]() не согласована относительно репера
не согласована относительно репера
![]() ,
т.е.
,
т.е.
![]() .
.
-
Согласуем систему векторов
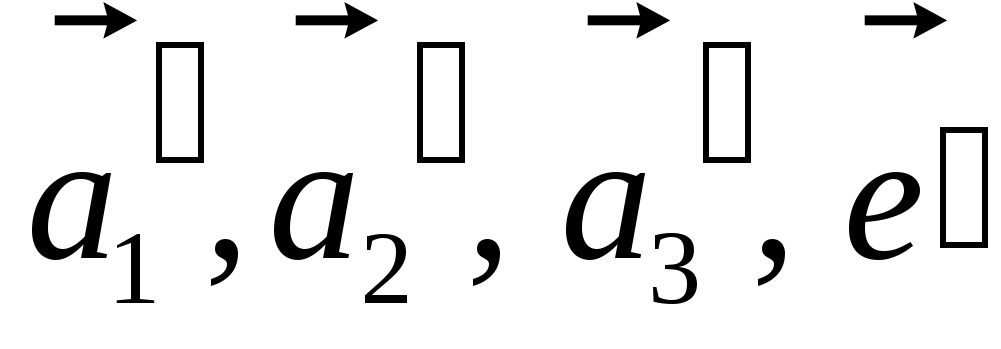 относительно репера
относительно репера
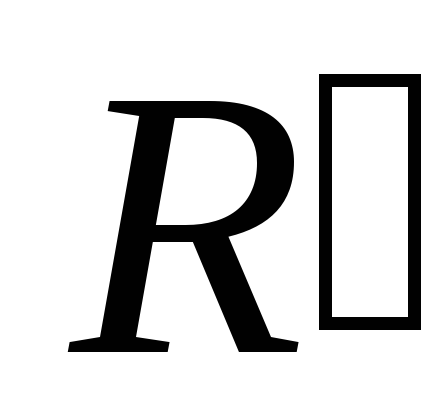 :
возьмем вместо векторов
:
возьмем вместо векторов
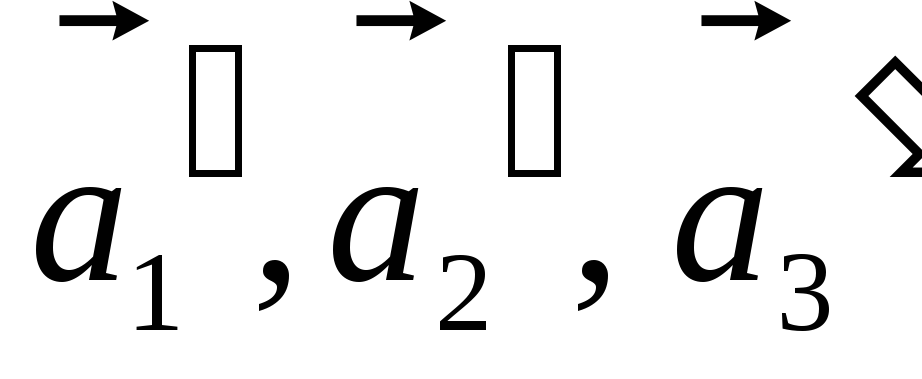 векторы
векторы
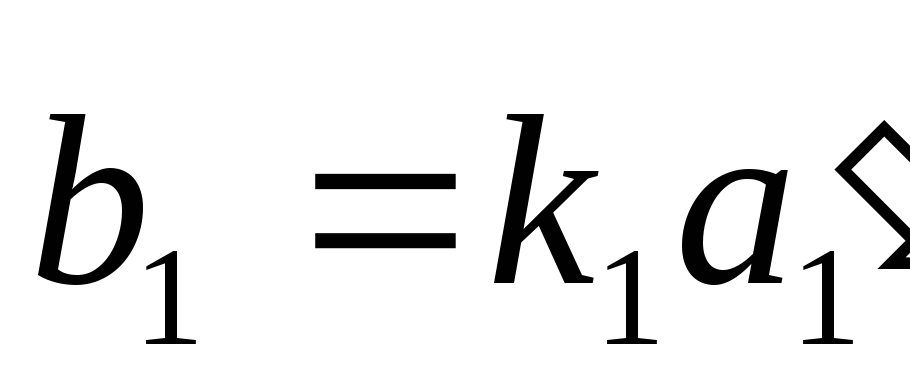 ,
,
 ,
,
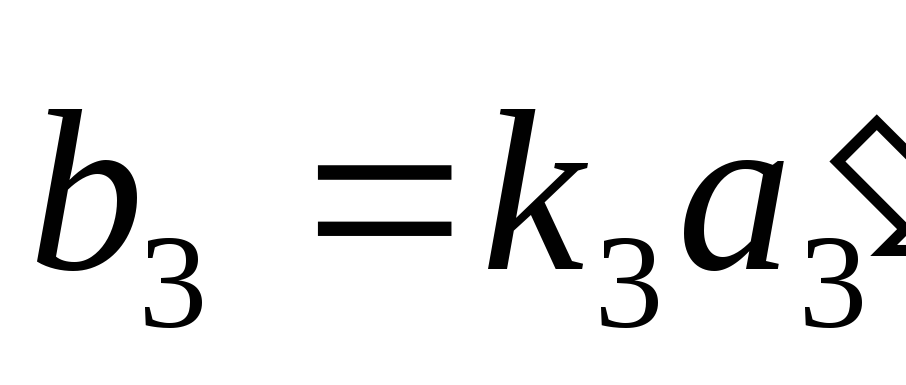 согласованные относительно репера
согласованные относительно репера
 и порождающие
точки
и порождающие
точки
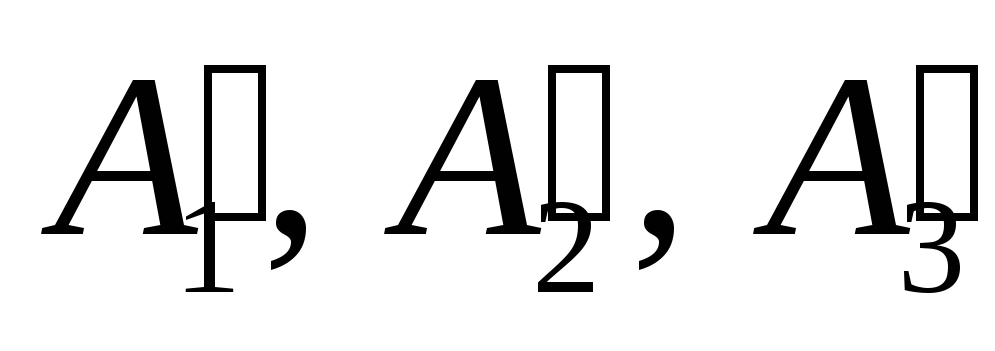 соответственно, т.е.
соответственно, т.е.
 (***).
(***). -
Запишем равенство (***)в координатной форме:
![]() ,
,
![]() ,
(****)
,
(****)
![]()
-
Рассмотрим (****) как систему с неизвестными
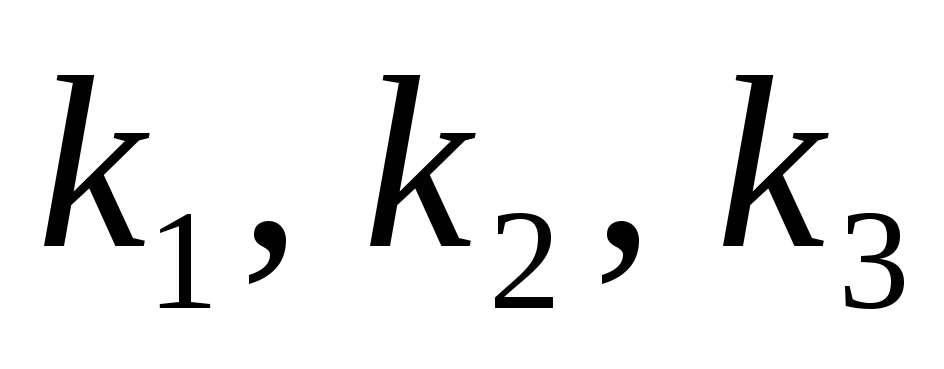 .
Так как система - неоднородна и
определитель отличен от нуля, то
.
Так как система - неоднородна и
определитель отличен от нуля, то
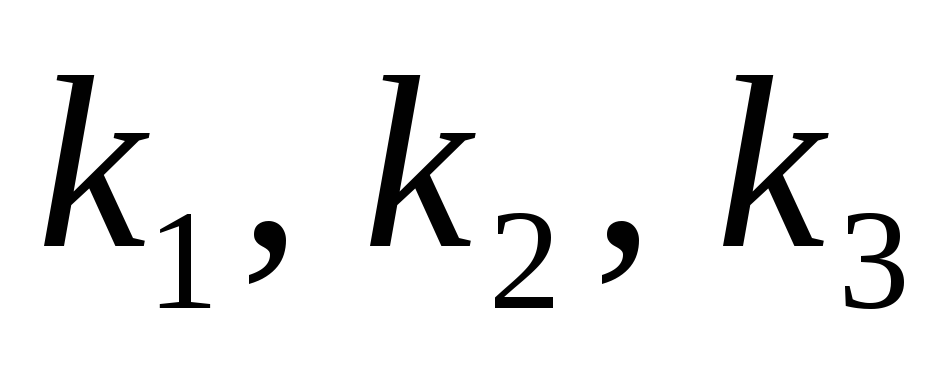 определяются однозначно, причем
определяются однозначно, причем
 не равны нулю одновременно.
не равны нулю одновременно. -
Матрица
 - матрица перехода от репера
- матрица перехода от репера
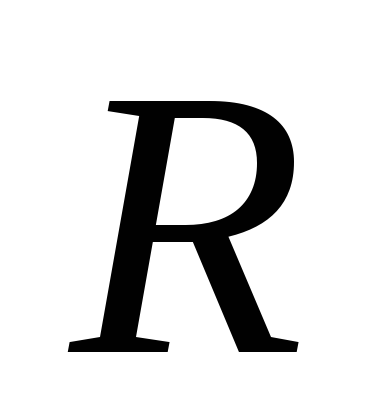 к реперу
к реперу
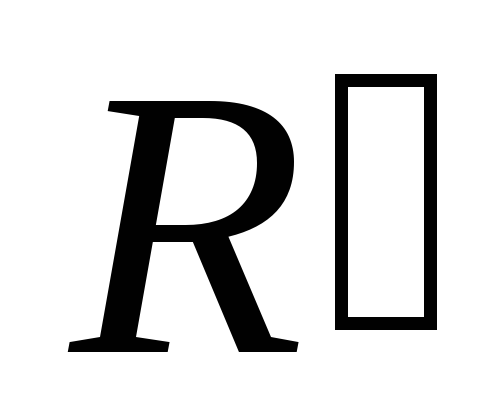
Замечание.
Аналогичные рассуждения приводят к
формулам преобразования координат на
проективной прямой:
![]()
![]() .
.
