Решение задач оптимизации с использованием MS Excel

Решение задач оптимизации с использованием MS Excel

С помощью инструмента «Поиск решения» решаются задачи оптимизации следующих типов.

1. Имеется функция одной или нескольких переменных и необходимо найти значения переменных, при которых функция равна либо минимуму или максимуму.

2. Имеется функция одной или нескольких переменных и необходимо найти значения переменных, при которых функция равна либо минимуму либо максимуму с учётом дополнительных ограничений.

Функция, значение которой отыскивается с помощью инструмента «Поиск решения» называется целевой функцией, а ячейка, где содержится формула для вычисления значений функции, называется целевой ячейкой.

Ограничение состоит из левой части, в которой содержится формула для вычисления некоторой величины, и правой части, в которой указывается величина ограничения. Левая и правая части соединяются либо знаком равенства, либо знаком неравенства.

Пример 1. Надо найти максимум функции при следующих ограничениях:

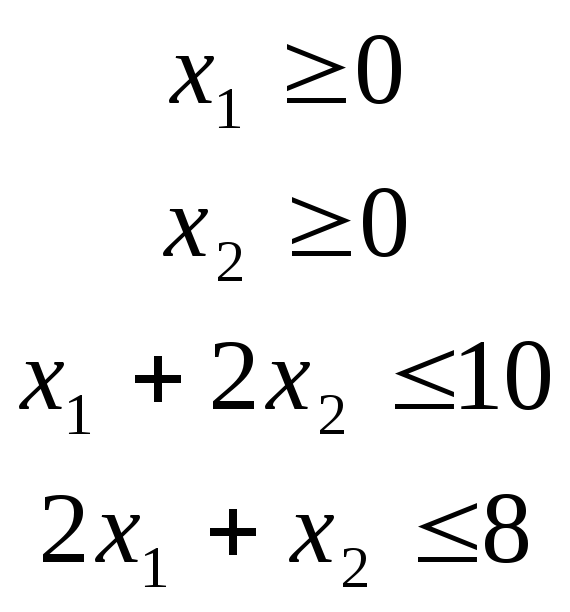
Эти данные можно внести на лист следующим образом:

	А	В
1	Переменные
2	Х1	Х2
3	0	0
4	Целевая функция
5	=300*А3+200*В3
6	Ограничения
7	=А3+2*В3	10
8	=2*А3+В3	8

После внесения исходных данных надо сделать активной целевую ячейку и вызвать «Поиск решения» через меню «Сервис\Поиск решения».

В появившемся диалоговом окне надо заполнить ряд полей.

Поле «Установить целевую ячейку» должно содержать адрес целевой ячейки. В нашем случае это адрес А5.

Затем установить переключатель «Равной» в положение «Максимальному значению».

Поле «Изменяя ячейки» должно содержать диапазон ячеек, содержащих независимые переменные. В нашем случае это А3:В3.

П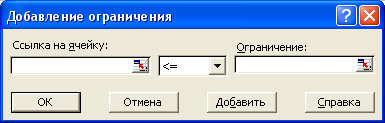оле «Ограничения» должно содержать все ограничения, если они имеются. В нашем случае, по условию задачи имеются четыре ограничения. Чтобы внести в это поле ограничения надо щелкнуть по кнопке «Добавить».

Появится диалоговое окно с тремя полями расположенными в ряд. Самое левое поле «Ссылка на ячейку», среднее поле со списком, и правое поле «Ограничение».

Поле «Ссылка на ячейку» должно содержать адрес ячейки с формулой ограничения. В поле со списком выбирается знак ограничения. Поле «Ограничение» содержит либо величину ограничения, либо адрес ячейки, где эта величина содержится.

В нашем случае, формула первого ограничения представляет собой просто переменную х1, поэтому указываем адрес А3, затем выбираем из списка неравенство больше или равно и величину ограничения указываем равной нулю. Чтобы добавить следующее ограничение надо в этом же окне щелкнуть по кнопке «Добавить» и внести новые данные. И так, до тех пор, пока не будут набраны данные по всем ограничениям. После внесения данных по последнему ограничению надо щелкнуть по кнопке ОК.

После этого можно щелкнуть по кнопке «Выполнить».

Через некоторое время появиться окно с результатом поиска решения. Возможны два варианта.

Если в окне будет сообщение «Решение найдено», то можно нажимать на кнопку ОК и в ячейках на листе будут содержаться найденные значения.

В нашем случае ячейки должны содержать: А3=2, В3=4, А5=1400, А8=10, А9=8.

Если появится сообщение «Процесс не сходится», то это означает, что решения не существует или оно не найдено при установленных параметрах поиска. Эти параметры можно изменить, если до щелчка по кнопке «Выполнить» нажать кнопку «Параметры». Можно попробовать изменить параметры «Максимальное время», «Предельное число итераций», «относительная погрешность» и «Допустимое отклонение».

Пример 2.

Авиакомпания М* по заказу армии должна перевезти на некотором участке 700 человек. В распоряжении компании имеется два типа самолетов, которые можно использовать для перевозки. Самолет первого типа перевозит 30 пассажиров и имеет экипаж 3 человека, второго типа – 65 и 5 соответственно.

Эксплуатация 1 самолета первого типа обойдется 5000$, а второго 9000$. Сколько надо использовать самолетов каждого типа, если для формирования экипажей имеется не более 60 человек.

Для начала, обозначим переменные: пусть X₁ – это оптимальное количество самолетов первого типа, X₂ – оптимальное количества самолетов второго типа. Очевидно, что стоимость эксплуатации самолетов должна быть минимальной. Следовательно,

5000X₁ + 9000X₂→min

Теперь определим ограничения. Для формирования экипажей имеется не более 60 человек, следовательно:

3X₁+5X₂<=60

Пассажиров надо перевезти не менее 700 человек, следовательно:

30X₁+65X₂>=700

Сформируем страницу электронной таблицы и постановку задачи линейного программирования в диалоговом окне:

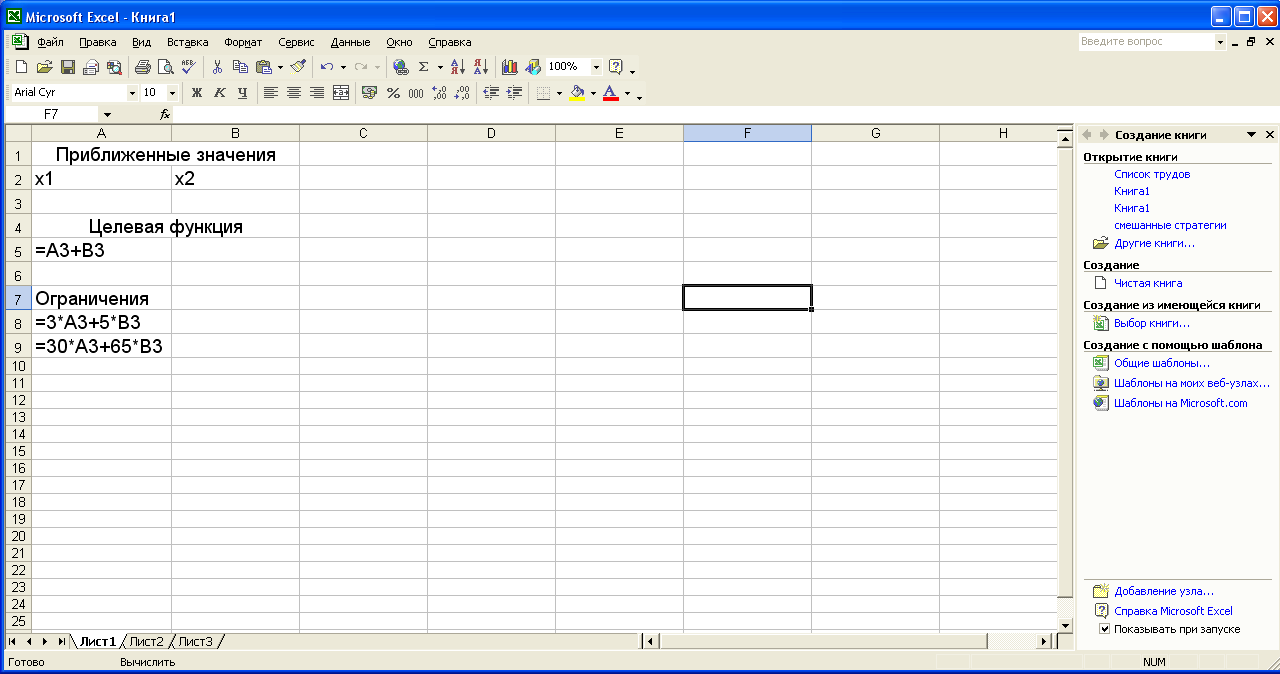
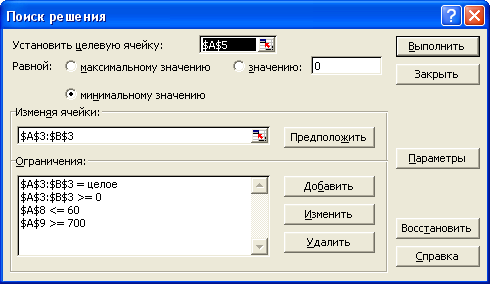
После выполнения поставленной задачи получаем следующие значения переменных. Как показано на рисунке

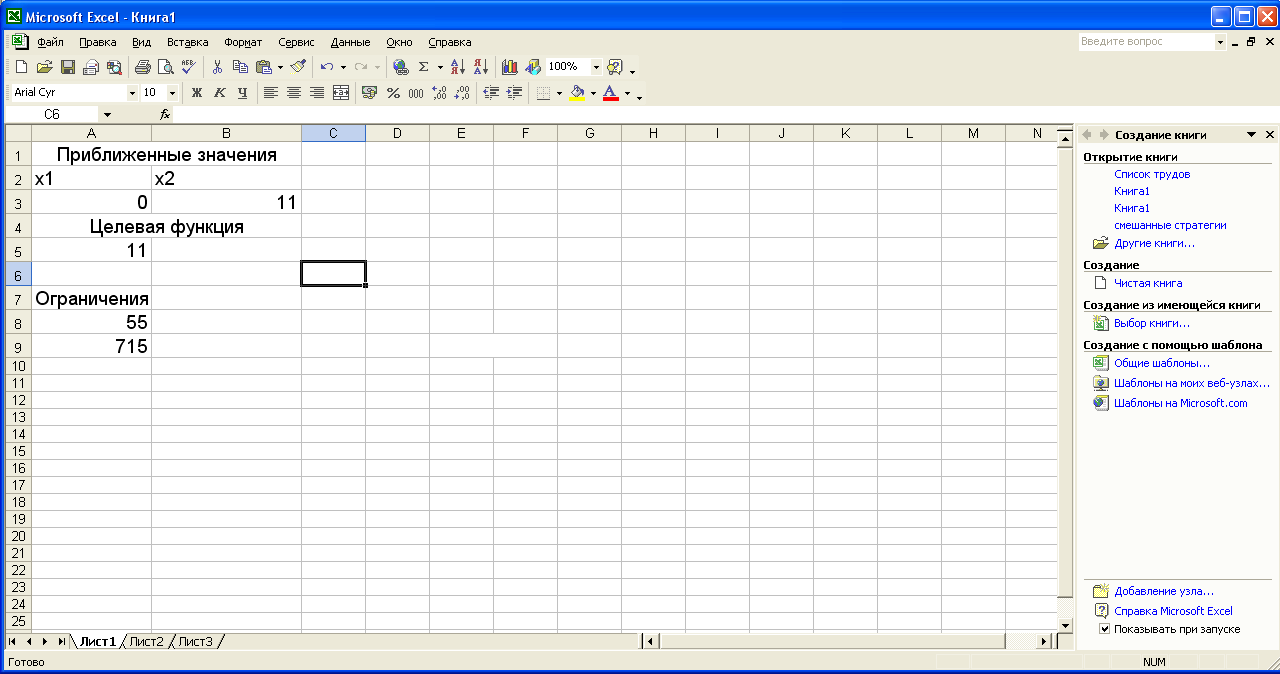
Т.е. нам необходимо (X₁=0) 0 самолётов первого класса и (X₂=11) 11 самолётов второго класса, для перевозки пассажиров.