
Электр. машины. / Электрические машины - книги / Электрические машины - Лекции
.pdfМинистерство образования и науки Российской Федерации Федеральное агенство по образованию
Государственное образовательное учреждение высшего профессионального образования
Северо-Западный государственный заочный технический университет
Кафедра электротехники и электромеханики
Е.П. Брандина
Электрические машины
Письменные лекции Примеры решения задач
Санкт–Петербург
2004
Е.П. Брандина
Электрические машины
Письменные лекции Примеры решения задач
Санкт–Петербург
2004
2
Утверждено редакционно-издательским советом университета УДК 621.313 (07)
Электрические машины. Письменные лекции. Примеры решения задач. -
СПб.: СЗТУ, 2004. - 152 с.
Рассматриваются принципы устройства, основные вопросы теории, режимы работ, эксплуатационные свойства трансформаторов и электрических машин. Приведены численные примеры решения задач.
Издание предназначено для студентов, изучающих дисциплины: ″Электромеханика″, ″Электрические машины″, ″Электрические машины специального назначения″, ″Электрические машины и аппараты″, ″Технические средства управления и информатики″.
Рассмотрено на заседании кафедры ″Электротехника и электромеханика″ 8.02.99 г., одобрено методической комиссией энергетического факультета
6.06.99 г.
Рецензенты: кафедра ″Электротехника и электромеханика″ СЗТУ (зав. Кафедрой профессор В.И.Рябуха); Ю.Ф.Кокунов, ст. преп. кафедры ″Электрические машины″ СПГПТУ.
Составитель : Е.П. Брандина, канд. техн. наук, доц
©Северо-Западный государственный технический университет, 2004
©Брандина Е.П. 2004
1.Трансформаторы
1.1.Общие сведения
1.1.1. Определение
Трансформатор - электромагнитный статический аппарат, который преобразует параметры переменного тока : напряжение, ток, частоту, число фаз .
В простейшем случае трансформа - тор представляет собой магнитопровод, с размещенными на нем двумя обмотками (рис.1.1).
Рис.1.1
1.1.2. Принцип работы
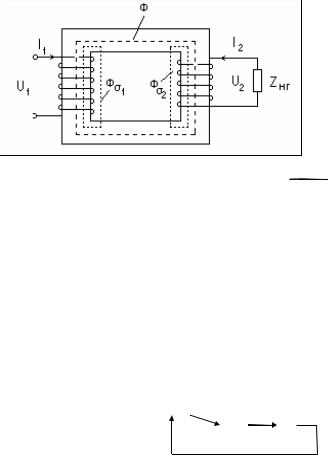
При включении первичной обмотки на переменное напряжение U1 возникает ток I1, который создает переменное магнитное поле. Это поле наводит в обеих обмотках ЭДС (Е1 и Е2 ). Если вторичную обмотку включить на нагрузку (ZНГ), то возникает ток I2. Основной магнитный поток Ф создается суммарным действием токов I1 и I2 (рис.1.2).
Е1
U1  I1
I1 Ф
Ф 
Е2 I2
Рис.1.2
1.1.3. Классификация трансформаторов
Классификация трансформаторов возможна по признакам [9] :
-по области применения (силовые, измерительные, специальные);
-по конструкции (стержневые, броневые, тороидальные),
-по способу охлаждения (сухие, масляные),
-по электрическим параметрам (по мощности, числу фаз, напряжению, частоте, числу обмоток).
Различают трансформаторы
-по числу фаз : однофазные, трехфазные и многофазные;
-по числу обмоток : двухобмоточные и многообмоточные;
-по напряжению: повышающие ( U2 > U1) и понижающие (U2 < U1).
Наибольшее применение находят силовые трансформаторы напряжения [ 9 ]. Суммарная мощность таких трансформаторов, установленных в электрических сетях, превышает мощность источников энергии в 7...10 раз. Это обусловлено необходимостью многоступенчатого повышения и понижения уровня напряжения.
Магнитопровод силового трансформатора выполняется шихтованным, т.е. набранным из отдельных листов электротехнической стали.
При f = 50 Гц толщина листов обычно составляет 0,5 мм, при повышении частоты толщина листов уменьшается. Шихтовка применяется для уменьшения потерь в стали на вихревые токи.
1.1.4. Схемы и группы соединения обмоток трансформатора
Для однофазного трансформатора возможны 2 случая намотки вторичной обмотки (рис.1.3 ) [1]. При этом ЭДС первичной обмотки Е1 и вторичной обмотки Е2 будут находиться соответственно в фазе или в противофазе. Группа соединения обмоток определяется углом сдвига фаз между первичным и вторичным линейными напряжениями. При этом вектор первичной линейной ЭДС эквивалентируется минутной стрелкой часов, расположенной на цифре 12, а вектор вторичной линейной ЭДС эквивалентируется часовой стрелкой. Таким образом , для однофазного трансформатора возможны две группы соединения: 0
и 6.
ГОСТ 11677-85 допускает для промышленного использования только нулевую группу соединения.
Рассмотрим трехфазный трансформатор при соединении первичных и вторичных обмоток в ‘’ звезду ’’ ( Y ) . Если одноименные фазы находятся на одном и том же стержне , то аналогично однофазному трансформатору получаем две группы соединений: 0 и 6. Если же одноименные фазы будут находится на разных стержнях, то получим остальной спектр четных групп: 2 и 8, 4 и 10. Например, на рис. 1.4 показано соединение обмоток для группы 0 [1]. При наличии вывода нулевой точки соединение обмоток обозначается Y0
Рассмотрим соединение фаз первичной обмотки в Y , а фаз вторичной обмотки в ″треугольник″ (∆). На рис. 1.5 показано соединение обмоток, соответствующее группе 11. Если поменять начала и концы фаз, например вторичной обмотки, то получим группу соединений 5. Если поменять местами фазировку, то можно получить все остальные нечетные группы: 7 и 1, 9 и 3 [1].
ГОСТ [ ] допускает для промышленного использования только 0 и 11 группы соединений . Итак, по ГОСТу предусматривается применение следующих групп: Y / Y0 - 0, ∆ / Y0 - 11, Y / ∆ -11, Y0 /∆ -11, Y/Z - 11.
Схема соединения Z (зигзаг) показана на рис. 1.6 [1]. Эта схема может применяться при несимметричной нагрузке фаз.
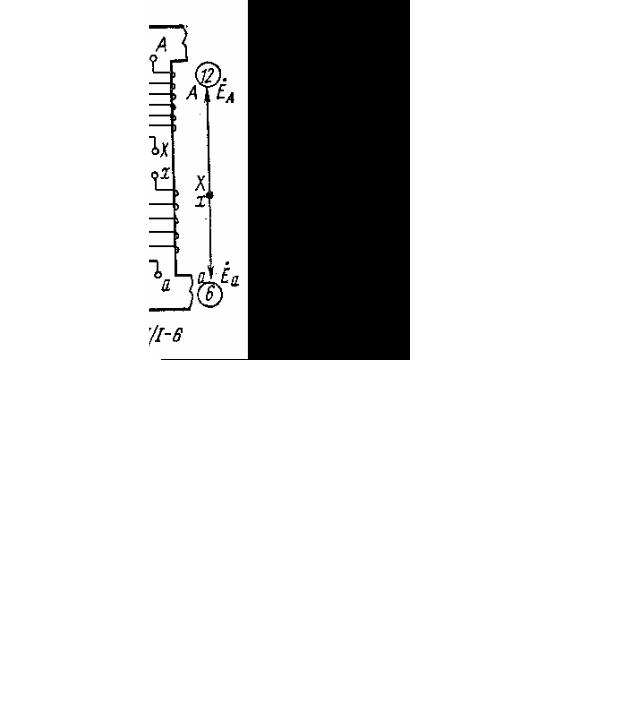
Рис.1.3
|
|
|
|
|
|
Рис.1.4 |
Рис.1.5 |
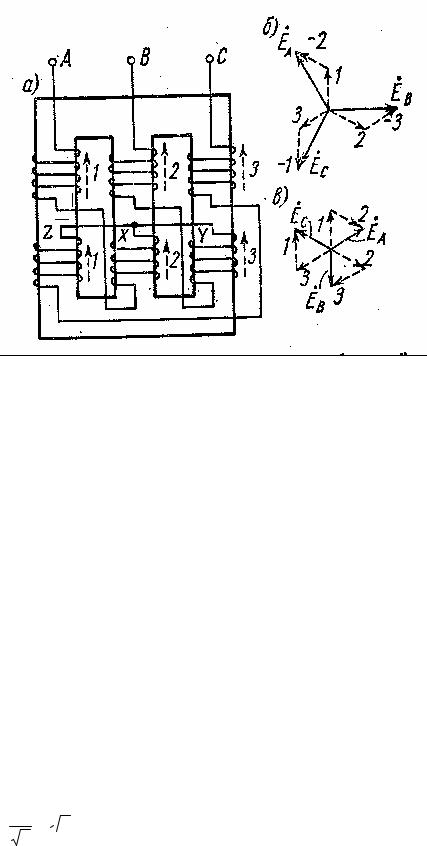
Рис. 1.6
1.2. Основные уравнения
1.2.1. ЭДС обмоток
По закону Максвелла ЭДС, индуктируемая в контуре с числом витков W переменным магнитным потоком Ф, равна
е = −W |
dФ |
, |
(1.1) |
|
dt |
||||
|
|
|
||
Примем, что Ф = Фm sin ωt , |
|
|||
где круговая частота |
ω = 2πf, |
|
||
|
|
|
||
f - частота питающей сети. |
|
|||
Тогда |
|
|
||
e = - WωФm cosωt = - W ωФm sin (90° -ωt) = WωФmsin(ωt - 90°) |
(1.2) |
|||
Амплитуда ЭДС |
|
|
||
Еm = WωФm
Действующее значение ЭДС
E = E2m =  2πfФmW ≈ 4,44 fФmW .
2πfФmW ≈ 4,44 fФmW .
(1.3)
Индекс ‘’ m ‘’ у потока Ф обычно опускают.
По фазе ЭДС Е отстает от потока Ф на 90° , что следует из сравнения формул (1.1) и (1.2).

На векторной диаграмме (рис.1.7) показано расположение векторов Е и Ф.
•Ф&
Е& Рис.1.7
Согласно (1.3) ЭДС первичной и вторичной обмоток имеют вид
Е1 = 4,44fФW1 ; |
|
|
|
Е2 = 4,44fФW2 |
|
|||||
Коэффициент трансформации |
|
|||||||||
k = |
E1 |
= |
|
W1 |
≈ |
U1 |
. |
(1.4) |
||
|
W |
|
||||||||
|
E |
2 |
|
U |
2 |
|
|
|||
|
|
|
2 |
|
|
|
|
|||
Обмотки трехфазного трансформатора могут быть соединены в «звезду» (Y) или в «треугольник» (∆) .
Соотношение линейных и фазных напряжений и токов:
для Y - U Л =  3 UФ , I Л = IФ ;
3 UФ , I Л = IФ ;
для ∆ - U Л =UФ , I Л = 3 IФ |
|
Полная мощность : |
|
однофазного трансформатора |
S =U I |
трехфазного трансформатора |
S = 3 UФ IФ = 3 U Л I Л |
Активная мощность нагрузки P = S cosϕ, реактивная мощность Q = S sinϕ,
где ϕ - угол нагрузки.
1.2.2. Уравнения напряжений
Магнитный поток трансформатора (рис.1.1) можно представить в виде основного магнитного потока Ф , созданного совместным
действием токов I1 и I2, |
и сцепляющегося с обеими обмотками, и |
||
потоков рассеяния Фσ1 и |
Фσ2 , каждый из которых создается только |
||
своим током (I1 |
Фσ1 и |
I2 |
Фσ2) и сцепляющихся только со своей |
обмоткой. Основной магнитный поток Ф наводит основные ЭДС Е 1 и Е2. Потоки рассеяния Фσ1 и Фσ2 наводят соответственно ЭДС рассеяния Еσ1 и Еσ2 (каждый поток - в своей обмотке).
Потокосцепление рассеяния ψσ = L i ,
где i = Im sinωt,
L - коэффициент самоиндукции обмотки.
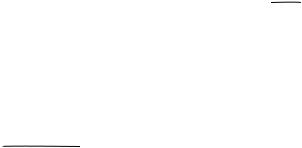
ЭДС рассеяния
eσ |
= − |
dψσ |
= −L |
di |
= −ω LIm cosω t = ω LIm sin(ω t − 90°) . |
|
dt |
dt |
|
||||
|
|
|
|
|
||
Действующее значение ЭДС в комплексном виде |
|
|||||
|
E&σ = − jxI = − jω LI& , |
(1.5) |
||||
где x = ωL - индуктивное сопротивление рассеяния (самоиндукции). Наличие (-j) в формуле (1.5) означает, что вектор ЭДС E&σ отстает по
фазе от вектора тока I& на 90°. Согласно (1.5) можно записать
E&σ1 = − jx1I&1 , E&σ 2 = − jx2 I&2 . |
(1.6) |
Применим закон Кирхгофа к первичной и вторичной обмоткам:
U&1 + E&1 + E&σ1 = I&1r1 , E&2 + E&σ 2 =U&2 + I&2 r2 .
С учетом (1.6) можно записать
|
U& |
= −E& |
+ I& |
r + jI& |
x |
1 |
, |
|
|
|
1 |
1 |
1 |
1 |
1 |
|
|
|
|
|
U&2 |
= E&2 − I&2 r2 − jI&2 x2 . |
|
|
|
(1.7) |
|||
где r1 и |
r2 -активные сопротивления обмоток |
||||||||
Полное сопротивление обмоток |
z1 = r1 + jx1 ; z2 = r2 + jx2. |
||||||||
Тогда |
U&1 |
= −E&1 + I&1 z1 |
, |
|
|
|
|
|
|
|
U&2 = E&2 − I&2 z2 . |
|
|
|
|
|
|||
1.2.3.Уравнение токов
Рассмотрим уравнение напряжения
U&1 = −E&1 + I&1 z1 .
Величина I1z1 для трансформаторов средней мощности составляет 5-10% U1, поэтому можно принять, что U1 ≈ E1 = 4,44 fФW. Так как напряжение сети U1=const, то отсюда следует, что поток , определяемый напряжением сети, Ф =const. Следовательно для всех режимов работы постоянна МДС, создающая этот поток.
МДС при нагрузке F& = I&1W1 + I&2W2 .
МДС при холостом ходе (х.х.) F = I10W1, где I10 - ток х.х. , I 2 = 0. Приравнивая эти МДС, получаем уравнение
I&1W1 + I&2W2 = I&10W1 .
Разделим на W1 и, с учетом k = W1 , получим уравнение токов
W2
& |
& |
1 |
& |
|
I1 |
+ I2 |
k |
= I10 . |
(1.8) |
1.3. Схема замещения. Приведенный трансформатор
Уравнения напряжений (1.7) и токов (1.8) позволяют определить все режимы работы трансформатора. Однако неудобство этих расчетов заключается в первую очередь, как правило, значительным отличием параметров и следовательно токов и напряжений первичной и вторичной обмоток, что затрудняет построение векторной диаграммы и т. д. Кроме того, в данном случае между обмотками существует не только электрическая, но и магнитная связь.
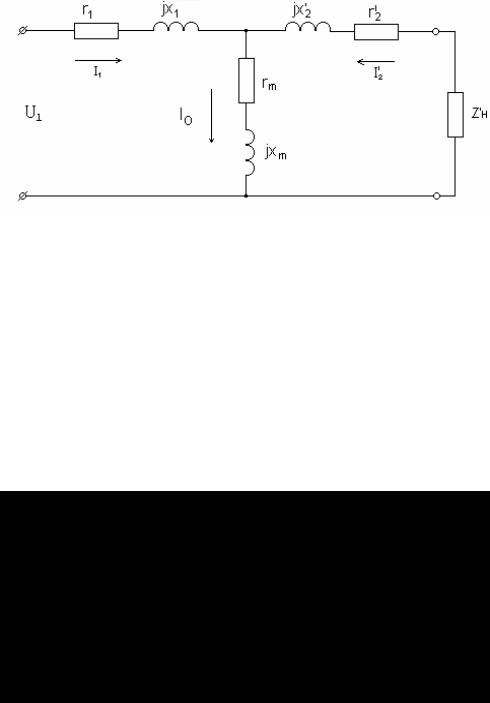
Для того, чтобы можно было связать первичную и вторичную обмотки электрически, устранить их магнитную связь и воспользоваться схемой замещения, принимают, что Е1 = Е2 и W1=W2 . Такой трансформатор называется приведенным. Параметры вторичной обмотки приведенного трансформатора обозначаются со штрихами. Схема замещения имеет вид, показанный на рис.1.8. Схема замещения относится к одной фазе
трансформатора. Параметры обмоток z1 и z2′ на схеме замещения выносят отдельно [2].
Рис.1.8
Активное сопротивление rm определяется потерями в стали
Pст = m1 Iо2 rm ,
где m1 - число фаз трансформатора.
Индуктивное сопротивление xm отражает взаимоиндукцию обмоток. Коэффициенты перехода от приведенного трансформатора к
реальному определяются из условия сохранения энергетических
