
- •Введение Модели и моделирование
- •Преимущества электрической энергии перед другими ее видами
- •Этапы развития электрической и электронной техники
- •Основные понятия и определения
- •Классификация электрических цепей
- •Топологические понятия теории электрических цепей
- •Электрические цепи постоянного тока Основные законы
- •Методы расчета электрических цепей
- •Пример расчет электрических цепей постоянного тока
- •Однофазные цепи синусоидального тока Общие сведения
- •Получение синусоидальной эдс
- •Основные параметры синусоидально изменяющихся величин
- •Представление синусоидального тока в различных формах
- •Активное сопротивление, индуктивность, емкость в цепях синусоидального тока
- •Последовательное включение активного, индуктивного и емкостного сопротивлений в цепи синусоидального тока. Резонанс напряжений
- •Параллельное соединение активного, индуктивного и емкостного сопротивлений в цепи синусоидального тока. Резонанс токов
- •Мощность цепи синусоидального тока
- •Расчет однофазных цепей синусоидального тока символическим методом
- •Пример расчета однофазной цепи синусоидального тока
- •Цепи периодического несинусоидального тока Основные характеристики несинусоидальных периодических токов и напряжений
- •Мощность цепи несинусоидального тока
- •Расчет электрической цепи с несинусоидальными эдс и токами
- •Пример расчет однофазной цепи периодического несинусоидального тока
- •Переходные процессы в линейных электрических цепях
- •Законы коммутации
- •Независимые и зависимые начальные условия
- •Характеристическое уравнение электрической цепи
- •Классический метод расчета переходных процессов
- •Переходные процессы вRl-цепях постоянного тока
- •Заряд и разряд конденсатора
- •Примеры расчета переходных процессов Расчет переходных процессов в цепях, содержащих активное сопротивление и индуктивность
- •Расчет переходных процессов в цепях, содержащих активное сопротивление и емкость
- •Литература Основная
- •Дополнительная
- •Приложение Моделирующий пакетElectronicsWorkbench ВозможностиElectronicsWorkbench
- •Компоненты и проведение экспериментов
- •КомпонентыElectronicsWorkbench
- •Технология подготовки схем
Параллельное соединение активного, индуктивного и емкостного сопротивлений в цепи синусоидального тока. Резонанс токов
Рассмотрим электрическую цепь синусоидального тока, содержащую две параллельно включенные ветви: одна содержит активно-индуктивное сопротивление, другая - активно-емкостное (рис. 32).
К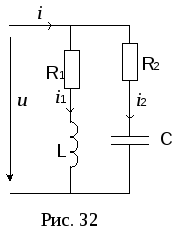 цепи подключен источник синусоидального
напряжения, изменяющегося по закону:
цепи подключен источник синусоидального
напряжения, изменяющегося по закону:![]() .
.
По I
закону Кирхгофа для мгновенных значений
токов:
![]() ,
а для комплексов -
,
а для комплексов -![]() Разделим обе части последнего уравнения
на одно и то же напряжение
Разделим обе части последнего уравнения
на одно и то же напряжение![]()
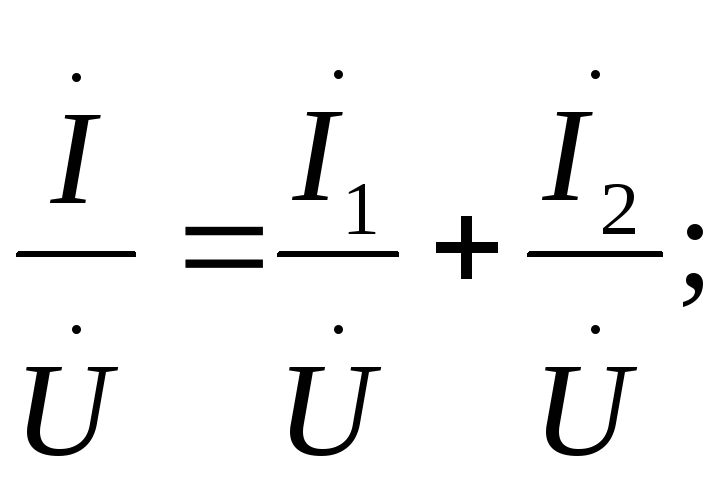
![]()
![]() ,
,
где
![]() -
полная проводимость.
-
полная проводимость.![]() ,
,![]() -
активная проводимость,
-
активная проводимость,
![]() - реактивная проводимость.
- реактивная проводимость.
![]() .
.
Если известны параметры цепи, то проводимости:
![]()
![]()
![]()
![]() .
.
Построим векторную диаграмму токов.
Пусть вектор приложенного напряжения
совпадает с положительным направлением
оси действительных чисел, т.е.
![]() (рис. 33). Ток
(рис. 33). Ток![]() отстает от
отстает от![]() на угол
на угол![]() ,
ток
,
ток![]() опережает
опережает![]() на
на![]()
У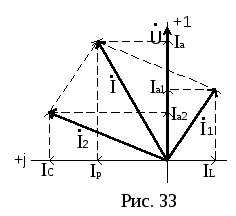 гол
сдвига фаз между током в неразветвленном
участке цепи и напряжением на концах
этого участка определяется следующим
образом:
гол
сдвига фаз между током в неразветвленном
участке цепи и напряжением на концах
этого участка определяется следующим
образом: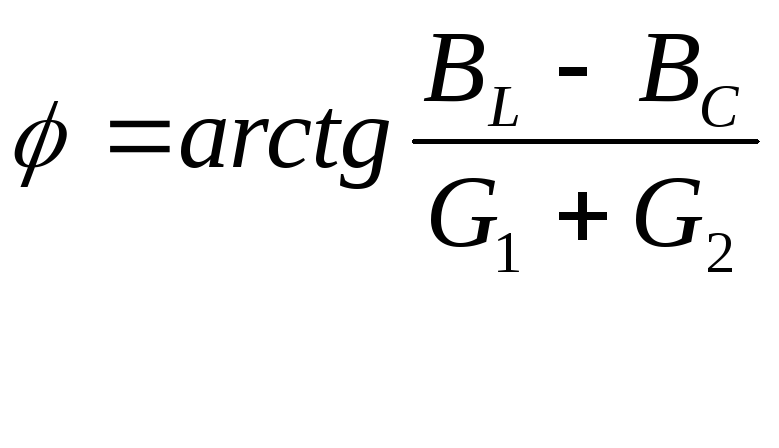 .
.
Проекции вектора тока в неразветвленной
части цепи на оси действительных и
мнимых чисел:
![]()
![]() .
Действующее значение этого тока
.
Действующее значение этого тока![]() .
.
Е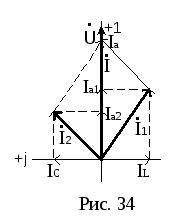 сли
сли![]() вектор тока отстает от вектора напряжения,
цепь носит активно-индуктивный характер.
вектор тока отстает от вектора напряжения,
цепь носит активно-индуктивный характер.
Если
![]() вектор тока опережает вектор напряжения,
цепь носит активно-емкостный характер.
вектор тока опережает вектор напряжения,
цепь носит активно-емкостный характер.
Если
![]() -
цепь носит активный характер, в цепи
наблюдается резонанс токов (рис. 34). При
этом
-
цепь носит активный характер, в цепи
наблюдается резонанс токов (рис. 34). При
этом![]() ,
,![]() ,
,![]() ,
,![]() .
.
Выводы:
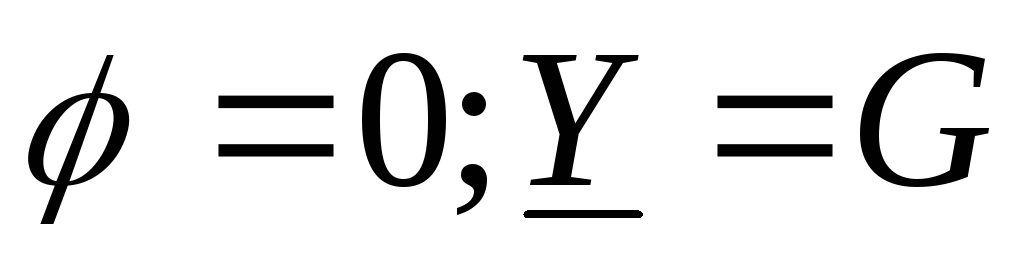 -
полная проводимость минимальна.
-
полная проводимость минимальна.Ток в неразветвленной части цепи минимален
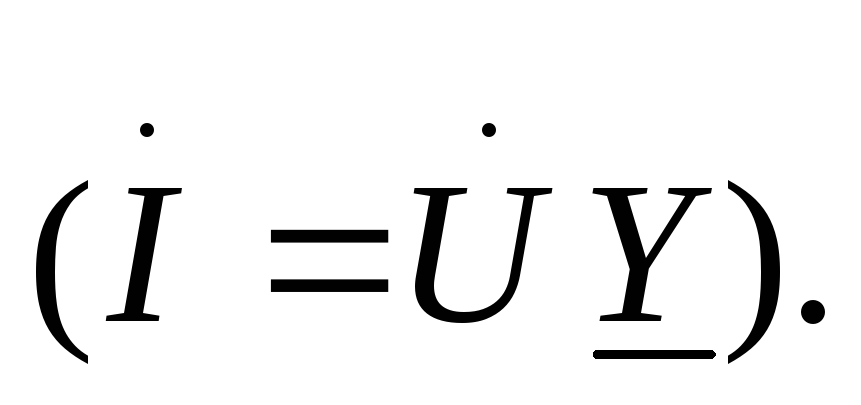
Если
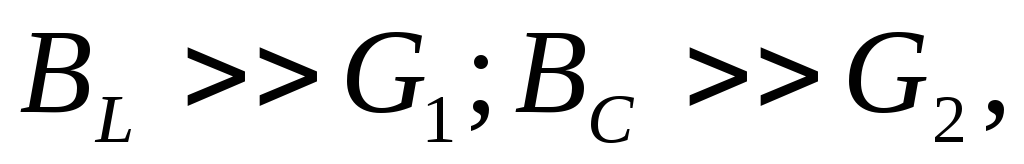 то
то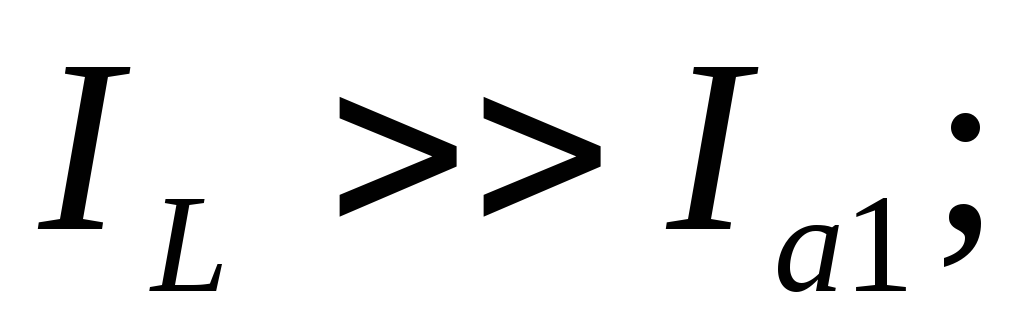
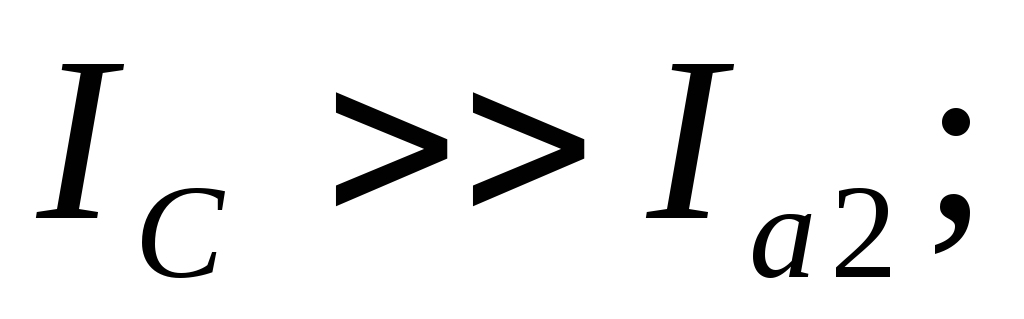
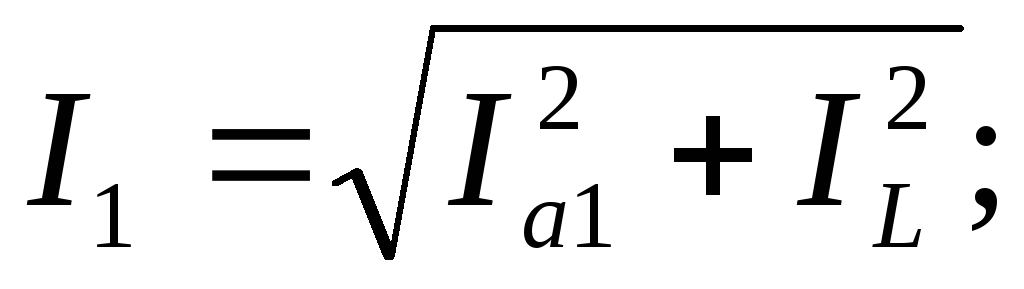
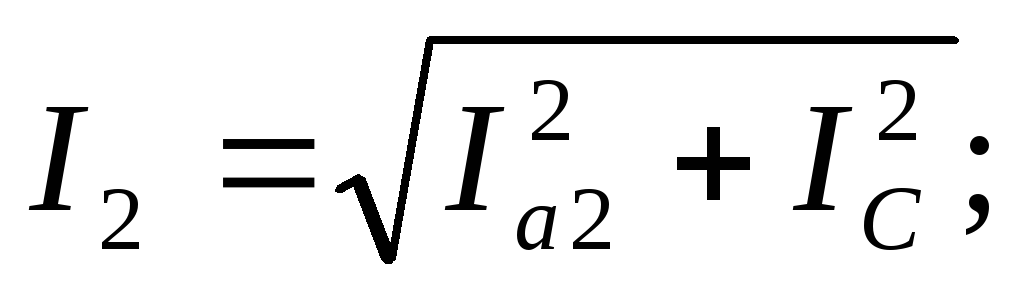
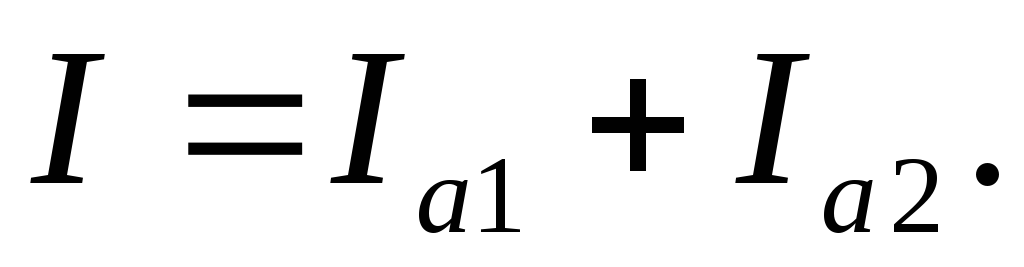 Следовательно,
Следовательно,
 то есть токи в ветвях значительно
больше, чем ток в неразветвленной части
цепи. Применяется в радиотехнике.
то есть токи в ветвях значительно
больше, чем ток в неразветвленной части
цепи. Применяется в радиотехнике.
Мощность цепи синусоидального тока
Под мгновенной мощностью (мощностью в данный момент времени) понимается произведение мгновенных значений тока и напряжения:
![]()
Если
![]() или
или![]() то
то![]() и в рассматриваемый участок цепи
поступает энергия.
и в рассматриваемый участок цепи
поступает энергия.
Если
![]() или
или![]() ,
то
,
то![]() и участок отдает энергию.
и участок отдает энергию.
Однако среднее значение мощности за период всегда положительное, т. к. на участке всегда есть необратимые преобразования энергии.
Средняя за период мощность называется активной и определяется следующим образом:
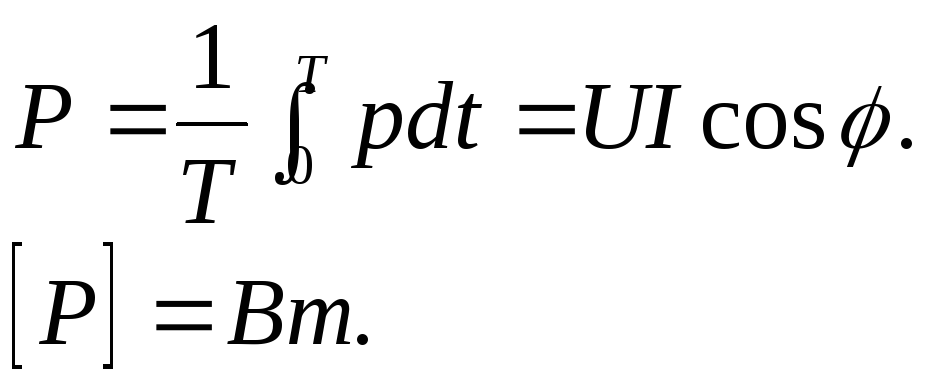
Мощность реактивных элементов
![]() в среднем за период равна 0, но в течение
четверти периода она положительна, что
физически означает накопление энергии
в магнитном поле катушки или в электрическом
поле конденсатора, а в течении следующей
четверти – отрицательна, что соответствует
расходу энергии.
в среднем за период равна 0, но в течение
четверти периода она положительна, что
физически означает накопление энергии
в магнитном поле катушки или в электрическом
поле конденсатора, а в течении следующей
четверти – отрицательна, что соответствует
расходу энергии.
Таким образом, имеет место процесс колебания энергии, но необратимых преобразований энергии нет.
Мощность колебаний энергии называют реактивной:
![]()
![]() -
(вольт-ампер реактивный).
-
(вольт-ампер реактивный).
Кроме
активной и реактивной мощностей цепь
синусоидального тока характеризуется
и полной мощностью
![]() Это максимально возможная мощность при
заданных напряжении
Это максимально возможная мощность при
заданных напряжении![]() и токе
и токе![]()
![]()
![]() .
.
Связь между различными мощностями:
![]() ,
,![]() .
.
В комплексной форме полная мощность
определяется следующим образом:
![]()
где
![]() сопряженный ток;
сопряженный ток;![]() ;
;![]()
![]()
Расчет однофазных цепей синусоидального тока символическим методом
Суть метода: если в цепи переменного тока токи, напряжения, сопротивления записаны в комплексной форме, то для этих цепей справедливы законы и методы расчета цепей постоянного тока.
Порядок расчета:
Записать в комплексной форме сопротивления всех ветвей.
Задать направление на комплексной плоскости известного тока или напряжения; представить в комплексной форме этот ток или напряжение.
Любым способом определить комплексы остальных токов и напряжений.
Правильность решения проверить, составив уравнения баланса активной и реактивной мощностей.
Смоделировать данную электрическую цепь средствами моделирующего пакета ElectronicsWorkbench, определить показания приборов, сравнить полученные результаты с расчетными, сделать выводы.
