
Elektromagnetizm_Optika_2006
.pdf
Оптическая разность хода интерферирующих лучей 2d 2 при этом учтено, что при отражении от пластинки фаза волны меняется на , а разность хода на 2 .
Запишем условия максимумов и минимумов интерференции соответственно
2dm / 2 |
m, |
где m=1,2… |
(2) |
|
2dm / 2 |
(2m 1) / 2, |
где m=0,1,2… |
||
|
Выражая d m из (2) и подставляя в (1), получим формулы расчѐта
радиусов тѐмных и светлых колец Ньютона, наблюдаемых в отражѐнном свете:
r 2 |
(2m 1)R / 2, |
(для светлых колец) |
(3) |
m |
|
|
|
r 2 |
mR, |
(для тѐмных колец) |
(4) |
m |
|
|
|
Так как между линзой и пластинкой в точке касания всегда остаѐтся зазор (менее / 4 ), то, для исключения его влияния, вычтем из уравнения, записанного для m-го кольца, то же уравнение, записанное для k-го кольца. В результате получим расчѐтную формулу:
r 2 |
r 2 |
(m k)R |
(5) |
m |
k |
|
|
Для наблюдения интерференционных эффектов необходимо, чтобы волны при наложении имели одну и ту же частоту, и чтобы разность фаз между ними оставалась постоянной (такие волны называются когерентными). Однако волны от обычного (не лазерного) источника света лишь частично когерентны. Поэтому чѐткая интерференционная картина будет наблюдаться при выполнении следующих условий:
1)Расстояние между лучами должно быть меньше радиуса
когерентности ког / , что ограничивает угловой размер источника света .
2)Разность хода лучей должна быть меньше длины когерентности
ког |
2 / |
(6), |
что |
приводит к ограничению числа видимых колец m |
|
||
mmax |
/ , |
(7) |
|
где - интервал длин волн, пропускаемых светофильтром.
Порядок выполнения работы
1.Для наблюдения колец Ньютона включите осветитель. При необходимости картину колец сфокусируйте.
2.Положите на окуляр микроскопа красный фильтр и измерьте диаметры 4 -5 тѐмных колец в делениях шкалы. Используя цену деления шкалы (написана на микроскопе), рассчитайте радиусы колец.
3.Подсчитайте число видимых тѐмных колец.
4.Замените красный фильтр другим (по указанию преподавателя) и подсчитайте снова число видимых тѐмных колец.
5.Результаты измерений занесите в таблицу 1 рабочей тетради.
6.Рассчитайте радиус кривизны линзы по формуле (5), используя не менее 3 комбинаций пар радиусов колец Ньютона
7.Найдите среднее значение радиуса кривизны линзы - <R>.
8.Используя формулу (7), по числу видимых темных колец для каждого светофильтра определите полосу пропускания Δλ, то есть интервал длин волн, который воспринимается глазом как один цвет.
9.Результаты расчѐтов занесите в таблицу 2 рабочей тетради.
10.Сделайте выводы.
ЛАБОРАТОРНАЯ РАБОТА № 34 Определение длины световой волны и характеристик дифракционной
решетки
Цель работы: применение дифракции света для определения длины волны; оценка характеристик дифракционной решетки
Методика эксперимента
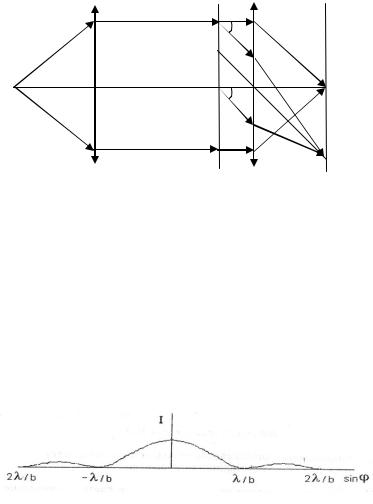
Экспериментальная установка (гониометр) состоит из источника света S, который помещают в фокусе линзы объектива 1, дифракционной решетки 2, окулярной линзы 3 и экрана 4, расположенного в фокальной плоскости окуляра (рис.34.1).
|
|
φ |
|
|
У |
|
|
|
|
|
глы |
S |
|
|
|
|
повор |
|
|
|
|
ота |
|
|
|
φ |
|
|
тубус |
|
|
|
|
|
а |
|
|
|
|
|
гонио |
|
|
|
|
|
метра |
|
|
|
|
|
с |
1 |
|
2 |
3 |
4 |
линзо |
й 3, равные углам дифракции, измеряют по шкале. |
|
Рис.34.1 |
|||
Расчет дифракционной картины от одной щели приводит к |
|||||
условию минимумов и максимумов соответственно: |
|
|
|||
b sin 2k , |
|
k 1,2,... , |
|
|
(1) |
2 |
|
|
|
|
|
b sin 2k 1 |
, |
k 1,2,... , |
|
|
(2) |
2 |
|
|
|
|
|
где b- ширина щели, λ- длина волны света, κ- порядок минимума и максимума интерференции.
Распределение интенсивности света при дифракции Фраунгофера от щели показано на рис.34.2
Рис.34.2
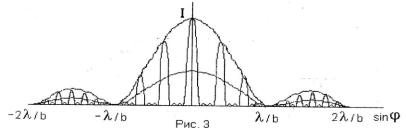
Дифракционная картина от дифракционной решетки при дифракции Фраунгофера аналогична рис. 2, но более сложная (рис.34.3).
Условие минимумов дифракционной решетки определяется |
||
|
|
дифрак |
|
|
цией |
|
|
света |
|
|
от |
|
|
одиноч |
|
|
ной |
|
|
щели, а |
|
Рис. 34.3 |
главны |
|
х |
|
|
|
|
максимумов и дополнительных минимумов – интерференцией света от различных щелей.
Условие главных максимумов для дифракционной решетки задаѐтся
уравнением: |
|
|
d sin k, |
k 1,2,..., |
(3) |
где d- период решетки, κ- порядок главных максимумов дифракции,- угол дифракции,
а условия минимумов – уравнением:
b sin k, |
k 1,2,... |
(4) |
Порядок выполнения работы
Задание 1. Определение длины световой волны
1.Включите осветитель и наблюдайте через окуляр гониометра дифракционный спектр.
2.Установите ноль шкалы на центральный максимум.
3.Поворачивая тубус гониометра, измерьте углы (в делениях шкалы), под которыми наблюдаются спектральные линии трехчетырех основных цветов (по заданию преподавателя) для порядка k=1 слева от центрального максимума.
4.Продолжая поворачивать тубус гониометра, проведите такие же измерения для порядка k=2 слева от центрального максимума.
5.Проведите аналогичные измерения для порядка k=1 и k=2 справа от центрального максимума.
6.Результаты измерений занесите в таблицу 1 рабочей тетради.

7. Рассчитайте длину волны для каждого цвета для k=1 и k=2 по формуле
d sin
k
(5)
(d – задано на установке). Определите среднюю длину волны для каждого цвета.
8. Результаты расчетов занесите в таблицу 2 рабочей тетради.
Задание 2.
Определение угловой дисперсии и оценка разрешающей способности решетки
1.Измерьте углы дифракции двух близко расположенных участков спектра одного цвета и одного порядка (в радианах).
2.Определите 1 и 2 , соответствующие углам дифракции 1 и 2 по формуле (5) и найдите 2 1 и 1 2
3.Данные измерений занесите в таблицу 3 рабочей тетради.
4.Определите дисперсию по формуле: D1 .
5. |
Рассчитайте |
дисперсию |
по |
формуле |
D2 |
k |
, |
||||||
|
|||||||||||||
d cos |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
где |
1 2 |
|
|
|
|
|
|
|
|
|
|||
2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
6. |
Рассчитайте |
разрешающую |
способность решетки |
по |
формуле |
||||||||
R k N для разных порядков. |
|
|
|
|
|
|
|||||||
7. |
Из формулы |
R |
|
для |
заданной |
длины волны λ |
найдите |
||||||
|
|
||||||||||||
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
наименьшую разность длин волн Δλ, которую может разрешить решетка в первом и во втором порядке.
8.Результаты расчетов занесите в таблицу 4 рабочей тетради.
ЛАБОРАТОРНАЯ РАБОТА № 35 Определение концентрации растворов сахара и постоянной вращения.
Методика эксперимента
Метод определения концентрации растворов основан на свойстве ряда веществ, называемых оптически активными, поворачивать на некоторый
угол плоскости колебаний векторов напряженности электрического поля E
и магнитного поля H . Это явление называется вращением плоскости поляризации. К числу веществ, способных поворачивать плоскость поляризации, относится сахар, оптическая активность которого обусловлена ассиметричным строением его молекул. В растворах оптически активных
веществ угол поворота плоскости поляризации |
пропорционален |
концентрации раствора C и длине пути света l в этом растворе. |
|
Cl , |
(1) |
где - постоянная вращения, величина которой зависит от строения молекул оптически активного вещества.
Зависимость (1) позволяет определить концентрацию раствора, если измерены угол φ и l. Для этого необходимо иметь поляризованный свет. Для его получения используется призма Николя. Она состоит из двух кристаллов исландского шпата, склеенных канадским бальзамом.
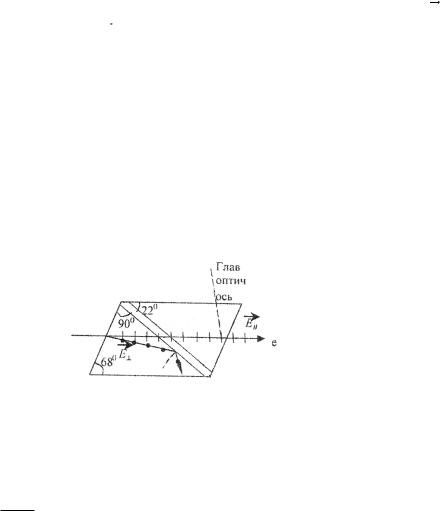
Рис.35.1 о
Луч естественного света разделяется в кристалле на два луча, поляризованные во взаимно перпендикулярных плоскостях. Один из них обыкновенный “o”, другой необыкновенный “e”. Необыкновенный луч не подчиняется законам преломления, его скорость и показатель преломления различны в разных направлениях:
sin n const sin e
Для обыкновенного луча |
sin |
n |
const , показатель преломления |
|
|||
|
sin |
0 |
|
|
|
|
n 0 не зависит от направления.
Клей подобран таким образом, что его показатель преломления имеет промежуточное значение между показателями преломления обыкновенного
луча – n0 и необыкновенного - |
ne |
ne < n < n0 |
(2) |
При падении на границу с клеем под углом, большим предельного, обыкновенный луч испытывает полное внутреннее отражение от оптически менее плотной среды (клея), а необыкновенный луч проходит через призму.
Таким образом, призма Николя является поляризатором: из неѐ выходит плоско поляризованный свет.
Прибор для определения концентрации растворов сахара называется сахариметром. Он позволяет измерить углы поворота плоскости поляризации . По графику зависимости от Сl, построенному с
помощью эталонных растворов, можно определить постоянную вращенияи концентрацию исследуемого раствора.
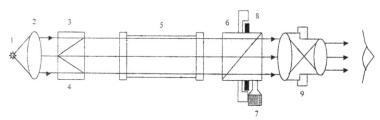
Принципиальная схема устройства полутеневого сахариметра представлена на рис. 35.2
Рис. 35.2
Свет от источника 1, находящегося в фокусе линзы 2, параллельным пучком попадает на поляризатор 3-4, после которого поляризованный свет проходит через трубку с раствором сахара 5, затем через анализатор 6 и, проходя систему линз в окуляре 9, попадает в глаз наблюдателя. Винт 7 служит для поворота анализатора 6. Отсчет угла поворота проводится по
шкале нониуса 8; Отсчет по шкале показан на рисунке 3
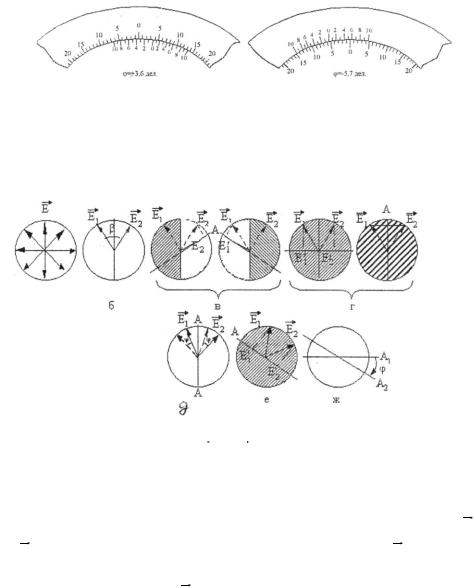
Рис. 35.3
Основными узлами прибора являются поляризатор (3,4) и анализатор
(6). Поляризатор состоит из двух призм Николя (3 и 4), позволяющих получить два пучка поляризованного света, в которых
Рис. 35.4
плоскости колебаний векторов E 1 и E 2 образуют между собой небольшой
угол β. (рис 35.4б). Анализатор – одна призма Николя, через которую проходят оба пучка света, выходящие из призм 3-4. Интенсивности обоих пучков после анализатора зависят от положения главной плоскости
анализатора А относительно направления колебания световых векторов E 1
и E 2 (рис 35.4в). Если плоскость А перпендикулярна E 1 , то левая половина поля зрения будет темной, правая – светлой.
Если А перпендикулярна E 2 , то правая половина поля зрения будет
темной, левая – светлой.
Если плоскость А расположена по биссектрисе угла β, то обе половины поля зрения будут освещены одинаково и ярко Если А расположить перпендикулярно биссектрисе угла β, то обе половины поля зрения будут

освещены одинаково и слабо (рис. 35.4г). В работе следует ориентироваться на слабую освещенность, так как к изменению еѐ глаз более чувствителен.
Если вставить между поляризатором и анализатором трубку с раствором сахара, то плоскости колебаний E 1 и E 2 повернутся на угол
и яркости полей изменятся. Чтобы восстановить одинаковую освещенность поля зрения, плоскость анализатора нужно повернуть на такой же угол
(рис.35.4д,е,ж).
Порядок выполнения работы
1.Определите начальный отсчет прибора при отсутствии в нем трубки с раствором. Для этого поверните анализатор винтом 7, найдите такое его положение, чтобы освещенность поля зрения менялась при повороте анализатора на небольшой угол: вначале левая половина светлая, правая темная, затем – наоборот. После этого установите анализатор в промежуточное положение, добиваясь одинаковой освещенности всего поля зрения.
Запишите отсчет по шкале. Измерение проведите три раза. Для этого поворотом винта слегка измените освещенность поля зрения и вновь добейтесь одинаковой освещенности обеих его половин.
2.В световой канал прибора вставляйте поочередно трубки с известной и неизвестной концентрацией сахарных растворов и для каждой трубки проведите три раза измерения угла, как описано в пункте1.
3.Результаты изменений занесите в таблицу 1 рабочей тетради.
4.Рассчитайте средние значения каждой серии измерений, затем вычтите из средних значений < > показания прибора без трубки с сахаром
< 0 >, получите углы поворота плоскости поляризации света каждым раствором.
5.Постройте график зависимости углов φ поворота плоскости поляризации растворов от произведения их концентрации С на длину трубок l.
6.Зная величину х угла поворота плоскости поляризации раствором
неизвестной концентрации, определите концентрацию по графику (рис.
35.5)
7. Определите постоянную вращения сахара по двум произвольно выбранным точкам на графике (рис.35.5)

2 1
(Cl) C2l2 C1 l1
Сl, % дм
С1l1 |
|
С2l2 |
|
|
|
Рис.35.5
