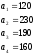- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
Вариант 19
Решить графическим методом задачу линейного программирования:

 max
max

Решить графическим методом задачу линейного программирования:

 min
min
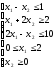
Для изготовления изделий вида А и В используются три типа технологического оборудования. В таблице приведены лимиты времени (в часах) работы на оборудовании каждого типа, выделяемые администрацией предприятия; нормативы затрат времени (в часах) на производство единицы изделия каждого вида на каждом виде оборудования. Известно, что прибыль от реализации одного изделия типа А составляет 18 ден. ед., а от реализации изделия типа Б - 10 ден. ед.
|
Типы оборудования
|
Лимиты времени (час.) |
Нормы расхода времени на изготовление одного изделия (час.) | |
|
Изделие А
|
Изделие В | ||
|
Оборудование 1-го типа
|
196 |
4 |
5 |
|
Оборудование 2-го типа
|
168 |
6 |
6 |
|
Оборудование 3-го типа
|
182 |
12 |
3 |
Составить план производства изделий А и В, обеспечивающий максимальную прибыль от их реализации.
1) Решить задачу графически.
2) Выполнить исследование на чувствительность полученного оптимального плана на основе графического решения. Для этого:
а) выявить активные и пассивные ограничения, дефицитные и недефицитные ресурсы;
б) как влияет увеличение запасов дефицитных видов ресурсов на оптимальное решение;
в) указать на сколько можно уменьшить запасы (лимиты) недефицитного ресурса без изменения оптимального плана и уменьшения дохода (в каждом случае менять запасы по одному виду ресурсов);
г) оценить границы изменения коэффициентов выражения целевой функции, при которых оптимальное решение не меняется.
3) Решить задачу симплексным методом.
4) Составить для данной задачи двойственную ей задачу и найти ее оптимальное решение.
Решить методом искусственного базиса задачу линейного программирования:

 min
min

Составить задачу, двойственную к данной

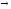 max
max

Составить задачу, двойственную к данной

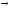 max
max

Решить задачу линейного программирования двойственным симплексным методом:

 max
max

Имеется m пунктов производства однородного груза
 иn
пунктов потребления груза
иn
пунктов потребления груза
 .
.
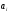 (тонн)
–количество
груза в пункте
(тонн)
–количество
груза в пункте
 ;
;
 (тонн)
- потребность в грузе пункта
(тонн)
- потребность в грузе пункта
 .
.
Известна
матрица затрат (тарифов)
 .
.
|
|
|
|
Найти оптимальный план перевозок.
По исходным данным транспортной задачи найти оптимальный план перевозок
|
|
|
|
Решить задачу № 9 при дополнительном условии: из второго пункта отправления груз должен быть вывезен полностью.