§ 12.14 Пондеромоторные силы
Обкладки конденсатора, заряженные разноимённо, притягиваются друг к другу.
Механические силы, действующие на макроскопические заряженные тела, называют пондеромоторными.
Рассчитаем пондеромоторные силы, действующие на обкладки плоского конденсатора. При этом возможны два варианта:
Конденсатор заряжен и отключён от заряженной батареи ( в этом случае количество зарядов на пластинах остаётся постоянным q = const).
При удалении одной обкладки конденсатора от другой совершается работа
dA=Fdx
за счёт которой увеличивается потенциальная энергия системы:
При этом dA = dW . Приравнивая правые части этих выражений, получаем
(12.67)
В данном случае при дифференцировании расстояние между пластинами обозначилось х.
Конденсатор заряжен, но не отключён от батареи (в этом случае при перемещении одной из пластин конденсатора будет сохраняться постоянным напряжение ( U = const ). В этом случае при удалении одной пластины от другой потенциальная энергия поля конденсатора уменьшается, так как происходит «утечка» зарядов с пластин, поэтому
Откуда
Но
,
тогда
Полученное
выражение совпадает с формулой
.
Оно может быть представлено и в другом
виде, если вместо зарядаq
ввести поверхностную плотность:
(12.68)
Поле
однородно. Напряжённость поля конденсатора
равна
,
где х – расстояние между пластинами.
Подставив в формулу
U2=E2x2,
получим, что сила притяжения пластин
плоского конденсатора
(12.69)
Эти силы действуют не только на пластины. Так как пластины, в свою очередь, давят на диэлектрик, помещённый между ними, и деформируют его, то в диэлектрике возникает давление
(S - площадь каждой пластины).
Давление, возникающее в диэлектрике, равно
(12.70)
Примеры решения задач
Пример 12. 5. К пластинам плоского воздушного конденсатора приложена разность потенциалов 1,5 кВ. Площадь пластин 150см2 и расстояние между ними 5 мм. После отключения конденсатора от источника напряжения в пространство между пластинами вставили стекло (ε2=7).Определите:
1) разность потенциалов между пластинами после внесения диэлектрика; 2) ёмкость конденсатора до и после внесения диэлектрика; 3) поверхностную плотность заряда на пластинах до и после внесения диэлектрика.
Дано: U1=1,5кВ=1,5∙103В; S=150см2=1,5∙10-2 м2; ε1=1; d=5мм=5∙10-3 м.
Найти: 1) U2; 2) С1 С2; 3) σ1, σ2
Решение.
Так
как
(σ-
поверхностная плотность зарядов на
обкладках конденсатора), то до внесения
диэлектрика σd=U1ε0ε1
и после внесения диэлектрика σd=U2ε0ε2,
поэтому
Ёмкость конденсатора до и после внесения диэлектрика
и
Заряд пластин после отключения от источника напряжения не меняется, т.е. q=const. Поэтому Поверхностная плотность заряда на пластинах до и после внесения диэлектрика
Ответ: 1) U2=214В; 2) С1=26,5пФ; С2=186пФ; 3) σ1= σ2=2.65 мкКл/м2.
Пример 12.7. Зазор между обкладками плоского конденсатора заполнен анизотропным диэлектриком, проницаемость ε которого изменяется в перпендикулярном к обкладкам направлении по линейному законуε = α + βх от ε1 до ε2, причём ε2 > ε1. Площадь каждой обкладки S, расстояние между ними d. Найти ёмкость конденсатора.
Дано: S; d; ε1; ε2
Найти: С.
Решение.Диэлектрическая проницаемостьε
изменяется по линейному закону , ε =
α + βх, где х отсчитывается от обкладки,
у которой проницаемость равна ε1.
Учитывая, что ε (0) = ε1, ε
(d) = ε2, получаем
зависимость
.
Найдём разность потенциалов между
обкладками:
Ёмкость конденсатора будет равна
Ответ:
Пример 12.7. Между пластинами плоского конденсатора, заряженного до разности потенциалов U , параллельно его обкладкам помещены два слоя диэлектриков. Толщина слоёв и диэлектрическая проницаемость диэлектриков соответственно равны d1, d2, ε1, ε2. Определите напряжённость электростатических полей в слоях диэлектриков.
Дано: U; d1, d2, ε1, ε2
Найти: E1, E2.
Решение.Напряжение на пластинах конденсатора, учитывая, что поле в пределах каждого из диэлектрических слоёв однородно,
U=E1d1+E2 d2. (1)
Электрическое смещение в обоих слоях диэлектрика одинаково, поэтому можем записать
D=D1=D2 = ε0 ε1E1= ε0 ε2E2 (2)
Из выражения (1) и (2) найдём искомое
(3)
Из формулы (2) следует, что
Ответ:
;
Пример 12.7. Площадь пластин S плоского конденсатора равна 100см2. Пространство между пластинами заполнено вплотную двумя слоями диэлектриков – слюдяной пластинкой (ε1=7) толщиной d1=3,5 мм и парафина (ε2=2) толщиной d2=5 мм. Определите ёмкость этого конденсатора..
Дано: S=100см2=10-2м2; ε1=7; d1=3,5мм=3.5∙10-3м;, ε1=2; d1=3,5мм=5∙10-3м;
Найти: С.
Решение.Ёмкость конденсатора
где = - заряд на пластинах конденсатора ( - поверхностная плотность заряда на пластинах); =- разность потенциалов пластин, равная сумме напряжений на слоях диэлектрика: U=U1+U2. Тогда
(1)
Напряжения U1 и U2 найдём по формулам
;
(2)
где Е1 и Е2 – напряжённость электростатического поля в первом и втором слоях диэлектрика; D - электрическое смещение в диэлектриках (в обоих случаях одинаково). Приняв во внимание, что
D = σ,
И учитывая формулу (2), из выражения (1) найдём искомую ёмкость конденсатора
Ответ: С=29,5пФ.
Пример 12.7. Батарея из трёх последовательно соединённых конденсаторов С1=1мкФ; С2=2мкФ и С3=4мкФ подсоединены к источнику ЭДС. Заряд батареи конденсаторов q =40мкКл. Определите: 1) напряжения U1, U2 и U3 на каждом конденсаторе; 2) ЭДС источника; 3) ёмкость батареи конденсаторов.
Дано: С1=1мкФ=1∙10-6Ф; С2=2мкФ=2∙10-6Ф и С3=4мкФ=4∙10-6Ф;q=40мкКл=40∙10-6Ф.
Найти: 1) U1, U2, U3 ; 2) ξ; 3) С.
Решение.При последовательном соединении конденсаторов заряды всех обкладок равны по модулю, поэтому
q1=q2=q3=q.
Напряжение на конденсаторах
ЭДС источника равна сумме напряжений каждого из последовательно соединённых конденсаторов:
ξ = U1+ U2 +U3
При последовательном соединении суммируются величины, обратные ёмкостям каждого из конденсаторов:
Откуда искомая ёмкость батареи конденсаторов
Ответ: 1) U1= 40В; U2= 20В, U3 = 10В; 2) Ɛ= 70В; 3) С= 0,571мкФ.
Пример 12.7. Два плоских воздушных конденсатора одинаковой ёмкости соединены последовательно и подключены к источнику ЭДС. Как и во сколько раз изменится заряд конденсаторов, если один из них погрузить в масло с диэлектрической проницаемостью ε=2,2 .
Дано: С1=С2= С;q=40мкКл=40∙10-6Ф; ε1=1; ε2=2,2.
Найти:
.
Решение. При последовательном соединении конденсаторов заряды обоих конденсаторов равны по модулю. До погружения в диэлектрик (в масло) заряд каждого конденсатора
где ξ = U1+ U2 (при последовательном соединении конденсаторов ЭДС источника равна сумме напряжений каждого из конденсаторов).
После погружения одного из конденсаторов в диэлектрик заряды конденсаторов опять одинаковы и соответственно на первом и втором конденсаторах равны
q= CU1=ε2CU2
(учли, что ε1=1), откуда, если учесть, что ξ = U1+ U2, найдём
(2)
Поделив (2) на (1), найдём искомое отношение
Ответ:
,
т.е. заряд конденсаторов возрастает в
1,37 раз.
Пример 12.7. Конденсаторы ёмкостями С каждый соединены так, как указано на рис.а. определите ёмкость Собщ этого соединения конденсаторов. .
Решение.
Если
отключить от цепи конденсатор С4,
то получится соединение конденсаторов,
которое легко рассчитывается. Поскольку
ёмкости всех конденсаторов одинаковы
(С2=С3
и С5=С6),
обе параллельные ветви симметричны,
поэтому потенциалы точек А и В, одинаково
расположенные в ветвях, должны быть
равны. Конденсатор С4
подключен, таким образом, к точкам с
нулевой разностью потенциалов.
Следовательно, конденсатор С4
не заряжен, т.е. его можно исключить и
схему, представленную в условии задачи,
упростить (рис.б).
Эта схема- из трёх параллельных ветвей, две из которых содержат по два последовательно включённых конденсаторов
Ответ: Собщ=2С.
Пример 12.7. Плоский воздушный конденсатор ёмкостью С1=4пФ заряжен до разности потенциалов U1=100В. После отключения конденсатора от источника напряжения расстояние между обкладками конденсатора увеличили в два раза. Определите: 1) разность потенциалов U2 на обкладках конденсатора после их раздвижения; 2) работу внешних сил по раздвижению пластин.
Дано: С1=4пФ=4∙10-12Ф; U1=100В;d2 =2d1.
Найти: 1) U2;2)A.
Решение. Заряд обкладок конденсатора после отключения от источника напряжения не меняется, т.е. Q=const. Поэтому
С1U1= С2U2, (1)
где С2 и U2 - соответственно ёмкость и разность потенциалов на обкладках конденсатора после их раздвижения.
Учитывая,
что ёмкость плоского конденсатора 
,
из формулы (1) получим искомую разность
потенциалов
(2)
После отключения конденсатора от источника напряжения систему двух заряженных обкладок можно рассматривать как замкнутую, для которой выполняется закон сохранения энергии: работа А внешних сил равна изменению энергии системы
А= W2 - W1 (3)
где W1 и W2 – соответственно энергия поля конденсатора в начальном и конечном состояниях.
Учитывая,
что
и
(q
– const),
из формулы (3) получим искомую работу
внешних сил
А=W2-
[учли, что q=C1U1 и формулу (2)].
Ответ: 1) U2=200В;2)A=40нДж.
Пример 12.7. Сплошной шар из диэлектрика радиусом R=5см заряжен равномерно с объёмной плотностью ρ=5нКл/м3. Определите энергию электростатического поля, заключённую в окружающем шар пространстве.
Дано: R=5см=5∙10-2м; ρ=5нКл/м3=5∙10-9 Кл/м3.
Найти: W.
Решение. Поле заряженного шара сферически симметрично, поэтому объёмная плотность заряда одинакова во всех точках, расположенных на равных расстояниях от центра шара.
Э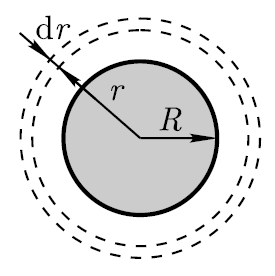
нергия
в элементарном сферическом слое (он
выбран за пределами диэлектрика, где
следует определить энергию) объёмомdV
(см. рисунок)
dW=ωdV, (1)
где
dV=4πr2dr
(r
– радиус элементарного сферического
слоя; dr
- его толщина);
(ε=1
– поле в вакууме; Е – напряженность
электростатического поля).
Напряжённость Е найдём по теореме Гаусса для поля в вакууме, причём в качестве замкнутой поверхности мысленно выберем сферу радиусом r (см. рисунок). В данном случае внутрь поверхности попадает весь заряд шара, создающий рассматриваемое поле, и, по теореме Гаусса,
Откуда
Подставив найденные выражения в формулу (1), получим
Энергия, заключённая в окружающем шар пространстве,
Ответ: W=6,16∙10-13Дж.
Пример 12.7. Плоскому конденсатору с площадью обкладок S и расстоянием между ними ℓ сообщён заряд q , после чего конденсатор отключён от источника напряжения. Определите силу притяжения F между обкладками конденсатора, если диэлектрическая проницаемость среды между обкладками равна ε.
Дано: S; ℓ; q; ε.
Найти: F.
Решение. Заряд обкладок конденсатора после отключения от источника напряжения не меняется, т.е. q=const. Предположим, что под действием силы притяжения F расстояние между обкладками конденсатора изменилось на d ℓ. Тогда сила F совершает работу
dA=Fdℓ (1)
Согласно закону сохранения энергии, эта работа равна убыли энергии конденсатора, т.е.
dA=-dW, (2)
откуда, исходя из выражений (1) и (2), получим
.
(3)
Подставив
в формулу для энергии заряженного
конденсатора
выражение для ёмкости плоского
конденсатора
,
получим
(4)
Подставив в формулу (3) значение энергии (4) и выполнив дифференцирование, найдём искомую силу притяжения между обкладками конденсатора
где знак «-» указывает на то, что сила F является силой притяжения.
Ответ:
Пример 12.7. Плоский конденсатор площадью обкладок S и расстоянием между ними ℓ подключен к источнику постоянного напряжения U. Определите силу притяжения F между обкладками конденсатора, если диэлектрическая проницаемость среды между обкладками равна ε.
Дано: S; ℓ; U; ε.
Найти: F.
Решение. Согласно условию задачи, на обкладках конденсатора поддерживается постоянное напряжение, т.е. U=const. Предположим, что под действием силы притяжения F расстояние между обкладками конденсатора изменилось на dℓ. Тогда сила F совершает работу
dA=Fdℓ (1)
Согласно закону сохранения энергии, эта работа в данном случае идёт на увеличение энергии конденсатора (сравните с предыдущей задачей), т.е.
dA=dW (2)
откуда, исходя из выражений (1) и (2), получим
(3)
Подставив
в формулу для энергии конденсатора
выражение
для ёмкости плоского конденсатора
,
получим
(4)
Подставив в формулу (3) значение энергии (4) и выполнив дифференцирование, найдём искомую силу притяжения между обкладками конденсатора
.
где знак «-» указывает на то, что сила F является силой притяжения.
Ответ:
