4.4 Поиск в глубину. Нахождение остовного дерева с помощью поиска в глубину.

Вход алгоритма: неориентированный граф и фиксированная вершина .

Выход алгоритма: компонента связности графа, в которую входит вершина .

Описание алгоритма: алгоритм передвигается по ребрам графа, оставляя пометки в вершинах графа. Начальную вершину пометим номером этой же вершины . Рекурсивный шаг алгоритма описывается следующим образом: Есть текущая вершина . Рассмотрим вершины графа, смежные с текущей. Если среди этих вершин найдется вершина без пометки (обозначим ее ), то передвигаемся в вершину и помечаем ее предыдущей вершиной .

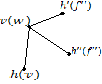
Если все вершины, смежные с вершиной помечены, то переходим обратно в вершину , которой была помечена текущая вершина . Алгоритм заканчивает свою работу тогда, когда текущей вершиной является начальная, а все смежные с ней вершины помечены.

Пример. Рассмотрим граф:

Начальная вершина . Выбираем смежные вершины: . Они непомечены. Двигаемся в любую из непомеченных вершин.

Возвращаемся обратно до тех пор, пока у текущей вершины есть непомеченные смежные с ней вершины.

Возвращаемся обратно.

Помеченные вершины - компонента связности.

Покажем корректность данного алгоритма.

Покажем, что отмеченные вершины есть компонента связности, в которой находится исходная вершина .

Пусть вершина была отмечена на некотором шаге алгоритма. Следовательно, эта вершина связана с исходной вершиной , т.к. по построению алгоритма движение происходило непрерывно по ребрам графа, и путь до исходной вершины из можно получить, двигаясь в обратном направлении по меткам вершин. Наоборот, существует вершина , связанная с вершиной . Покажем, что она будет помечена на некотором шаге алгоритма.

Предположим противное: вершина не была помечена алгоритмом. Рассмотрим первую вершину на пути из начальной вершины в вершину , которая не была помечена. Пусть это будет вершина . Вершину и все вершины между и помечены.

Рассмотрим последний шаг алгоритма, когда текущая вершина была . Тогда в очередной момент времени обязательно будет рассмотрена вершина, из которой была помечена вершина , т.е. происходило обратное движение при непомеченной смежной вершине.

Это противоречит построению алгоритма. Что и требовалось доказать.

Свойство алгоритма поиска в глубину.

Рассмотрим граф – исходный граф. Будем считать его связным. будем обозначать граф с тем же множеством вершин и множеством ребер (это ребра, по которым происходит движение алгоритма поиска в глубину хотя бы один раз). Тогда справедливо свойство:

– граф без циклов

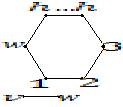
Рассмотрим произвольное ребро , по которому движение происходит хотя бы один раз, следовательно, либо вершина будет иметь метку , либо наоборот. Действительно, рассмотрим один момент, когда алгоритм проходил по ребру . Если это движение было из в , тогда вершина получила метку , либо наоборот – движение было из в , а вершина получила метку .

Предположим противное. содержит некоторый цикл. Пусть – первая вершина цикла, которую посетил алгоритм. Это значит, что метка вершины будет отлична от всех остальных вершин цикла. Тогда последовательно перебираем вершины цикла. Тогда, вершина должна иметь метку , вершина метку и т.д. Рассмотрим последнюю вершину в цикле. Она будет иметь метку предыдущей вершины . Следовательно, для каждой вершины ребра имеем противоречие с предложением выше. Метка каждой вершины отлична от и от , хотя по этому ребру проходило движение алгоритма.

Определение. Деревом называется связный граф без циклов.

Пример. Простая цепь есть дерево:

Утверждение. Минимальное число ребер в графе на вершинах (), которые обеспечивают связность графа равно .

Доказательство

1. Очевидно, что ребро достаточно, чтобы связать вершин. такое соединение есть цепь из последовательных ребра. Покажем, что меньшим числом ребер обойтись невозможно. Покажем это математической индукцией по числу вершин в графе. Для двух вершин в графе это очевидно. С двумя вершинами без ребер граф связным не является.

Допустим, утверждение доказано для вершин, т.е. минимальное число ребер для связности вершин будет равно . Рассмотрим вершину и предположим противное, что для вершины можно обойтись ребром, чтобы их связать. Рассмотрим соответствующий граф , , . Этот граф не имеет циклов (в противном случае можно удалить любое ребро из цикла и граф останется связным – любые две вершины соединены двумя не пересекающимися путями, следовательно, если граф содержит цикл, то можно было бы уменьшить число ребер, которые связывают вершины этого графа). Теперь покажем, что в связном графе без цикла обязательно существует висячая вершина (имеющая только одну смежную с ней вершину). Предположим противное – граф без циклов висячих вершин не имеет, т.е. каждая вершина смежна по крайней мере с двумя другими. Рассмотрим движение по ребрам графа. Из текущей вершины v передвигаемся в вершину отличную от той, из которой мы попали в v (так как число смежных вершин не менее двух, такое движение возможно

Как только попадем в вершину, где были ранее, остановимся. Не трудно видеть, что такая ситуация неизбежна в силу конечности числа вершин. В результате получим простой цикл – противоречие исходному графу.

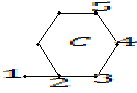
Таким образом, рассмотренный граф обязательно содержит висячую вершину . Удалим вершину вместе с ребром, инцидентным ей. Очевидно, в результате получается связный граф с числом ребер на вершинах, что противоречит предположению индукции (для связности вершин необходимо ребро).

Рассмотрим граф с числом вершин . Рассмотрим следующие 3 свойства графа:

1) Связность

2) Отсутствие циклов

3) Число ребер в графе (далее будем рассматривать графы без петель).

Утверждение. Любые два свойства из указанных порождают третье.

Доказательство:

(a)

Покажем, что связный граф на вершинах, не имеющий циклов, содержит ребро. То есть, любое дерево на вершинах имеет ребро. Доказательство будем проводить по индукции по числу вершин в дереве.

Дерево с единственной вершиной не имеет ребер. Допустим, что доказано, что любое дерево на вершинах имеет ребро. Рассмотрим дерево на вершине. Как было замечено раньше, в любом дереве есть висячая вершина, т.е. вершина, которой инцидентно не более чем одно ребро. Удалим висячую вершину вместе с инцидентным ребром из дерева . В результате получим граф , который является связным и без циклов. По предположению индукции, число ребер в этом графе равно . Поэтому, в первоначальном дереве число ребер равно .

Что и требовалось доказать.

(b)

Покажем, что связный граф на вершинах, содержащий ребро не имеет циклов.

Предположим противное: рассматриваемый граф содержит цикл . Удалим какое-либо ребро из данного цикла. При этом связность графа не нарушится, т.к. любая пара вершин в цикле графа соединена не пересекающимися путями в цикле. Поэтому полученный граф будет связным, имеющим то же число вершин , и ребра. Получаем противоречие с тем, что минимальное число ребер для связности графа на вершинах равно .

Что и требовалось доказать.

(c) 2

Покажем, что граф на вершинах и ребре, в котором отсутствуют циклы, является связным.

Предположим противное: рассматриваемый граф не является связным. Рассмотрим компоненты связности графа с числом вершин в компонентах связности соответственно. Компоненты связности являются деревьями, т.к. это связные графы без циклов. Поэтому, по доказанному, компоненты связности имеют соответственно ребро. Тогда общее число ребер в таком графе равно

Так как граф не связный, то число компонент связности равно, по крайней мере, двум, то есть, . Поэтому число ребер , что противоречит третьему свойству нашего графа: число ребер в нем равно .

Что и требовалось доказать.

Таким образом, любые два из перечисленных трех свойств можно взять за основу определения дерева.

Рассмотрим граф .

Определение. Подграфом графа называется граф , где , а . Причем каждое ребро из подмножества имеет оба конца в множестве .

Определение. Пусть граф связный. Тогда остовным деревом графа называется подграф графа на том же самом множестве вершин , который является деревом.

Пример. Рассмотрим граф на множестве, состоящем из вершин. Остовным графом этого графа является граф, представленный справа:

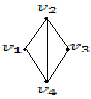
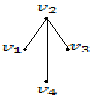
Утверждение. Любой связный граф имеет остовное дерево.

Доказательство:

Остов связного графа можно получить поиском в глубину, а именно, рассматривая все ребра , которые были пройдены алгоритмом поиска в глубину. Все такие ребра содержат все вершины графа, и данное множество ребер не содержит циклов. Также остовное дерево связного графа можно получить последовательно удаляя ребра из имеющихся в графе циклов до тех пор, пока не получится граф без циклов.