Все полные системы для классов t0, t1, s, m, l в утверждениях выше являются базисами для этих систем.

Доказательство:

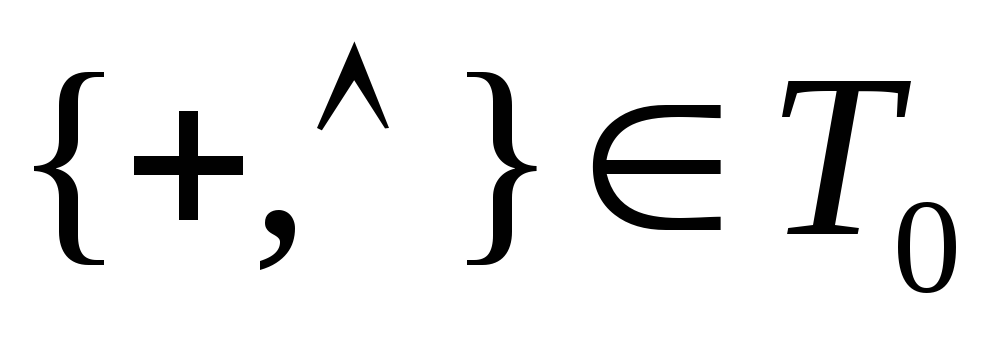1. - эта система полна в Т₀ . Покажем, что любая собственная подсистема полной в Т₀ не является. Рассмотрим . Т.к.,тогда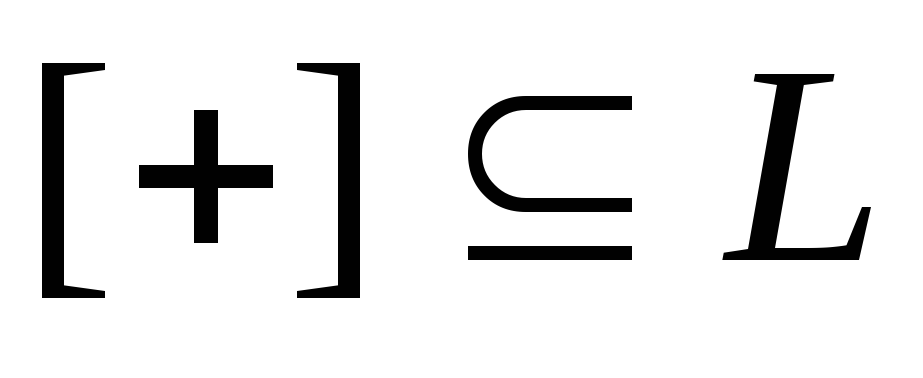, но функция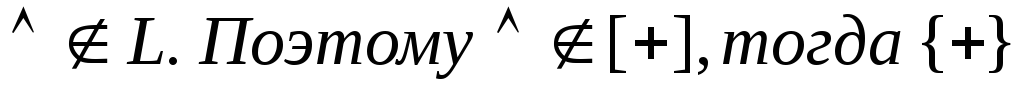не является полной в классеТ₀ .

Рассмотрим в силу того, чтоне является полной в классеТ₀ . Таким образом все собственные подсистемы не полны в классе Т₀, поэтому - базис вТ₀ .

2) 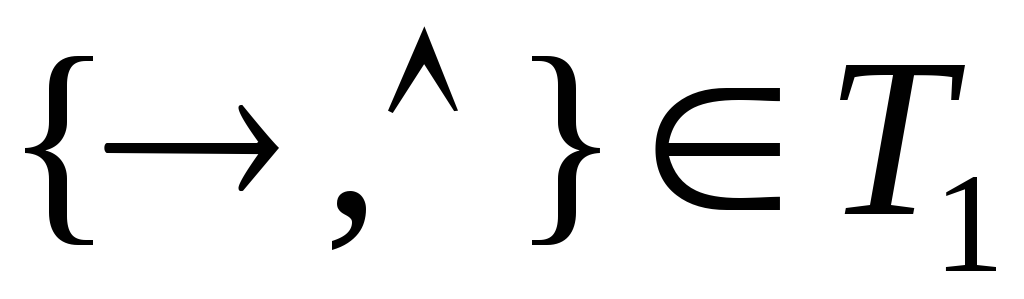- эта система полна вТ₁ . Покажем, что все собственные подсистемы не полны в Т₁. Покажем, что не полна вТ₁ , а именно . Для этого рассмотрим классК следующих функций: , если и только если для любых 2-х наборов значений переменных, на которых значение функции равно 0 существует переменная равная 0 в обоих наборах, причем наборы не обязательно различные:

Например

0 0 1 1 0 0

0 1 1 1 0 0

1 0 0

1 1 1 в обоих наборах.

Из определения следует, что на единичном наборе функция из К равна единице.

0 0 0

0 1 1

1 0 1 0 0 в обоих наборах

1 1 1 0 0

0 0 0

0 1 0 0 1

1 0 0 1 0

1 1 1

Утверждение:

Класс К замкнут относительно суперпозиции функций.

Доказательство: Пусть

Образуем их суперпозицию:

Пусть верно противное - суперпозиция , тогда существует пара наборов значений переменных

:

для любогои для любого

Обозначим

.

Тогда на обоих наборах значениеравно 0. В силу того, что, и т.к. в наборахнет переменной, равной нулю, такой переменной должна быть последняя переменная, т. е.. Но для наборовнет переменной, равной нулю в обоих наборах, следовательно получаем противоречие с тем, что. Утверждение доказано.

В силу того, что . Но.

Рассмотрим в силу того, что, имеем,. Таким образом все собственные подсистемы системыполными вТ₁ не являются, и тогда является базисом вТ₁ .

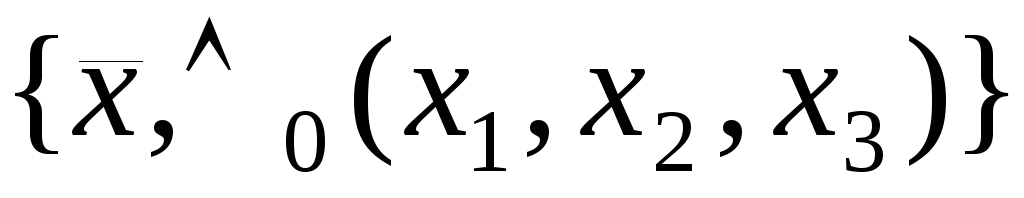2. есть базис в S. Эта система полна в классе S. Покажем, что все собственные подсистемы данной системы в классе S полными не являются - эта функции у которых ровно одна существенная переменная, а функция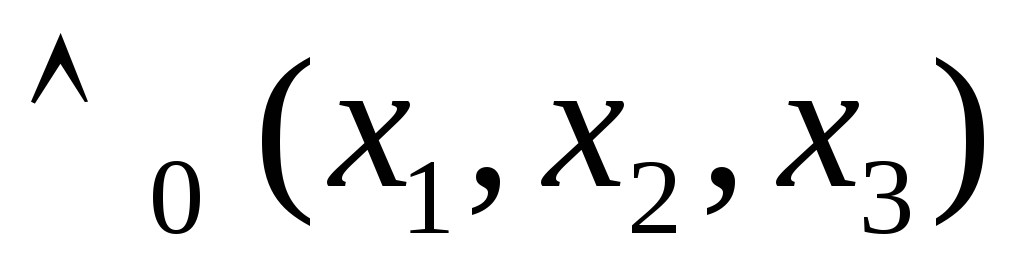имеет три существенные переменные. Поэтому.

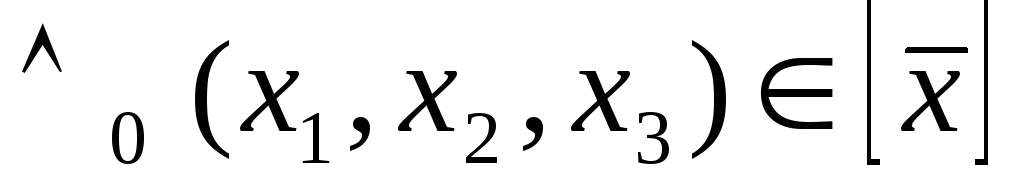3. Рассмотрим функцию

, поэтому система - базис вS .

4) Покажем, что 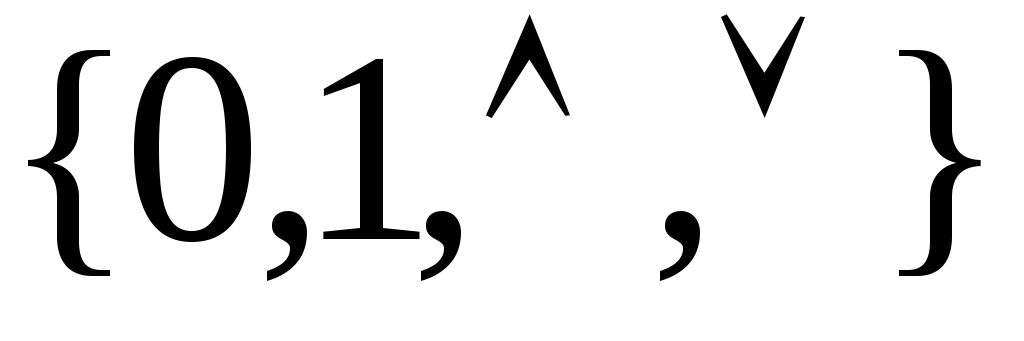- базис вМ. Во-первых эта система полна в классе М . Покажем, что все собственные подсистемы не полные.

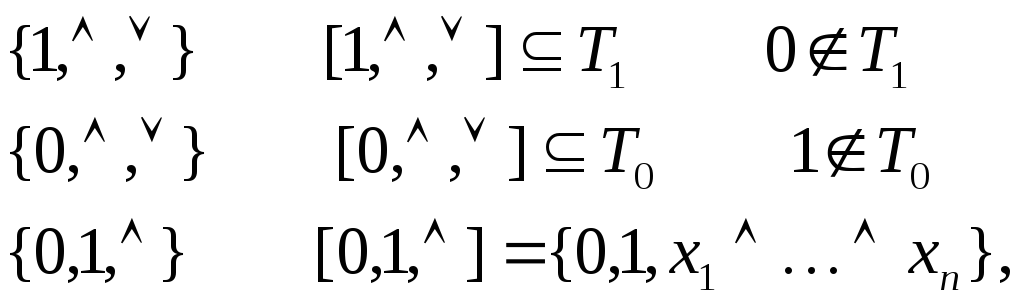
а функции дизъюнкции в замыкании нет поэтому система 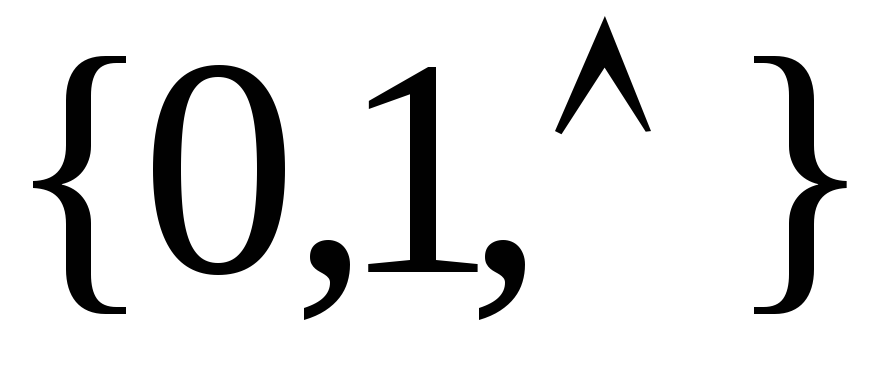не полна в классеМ.

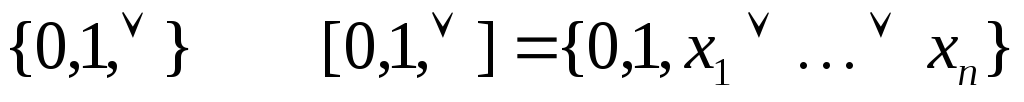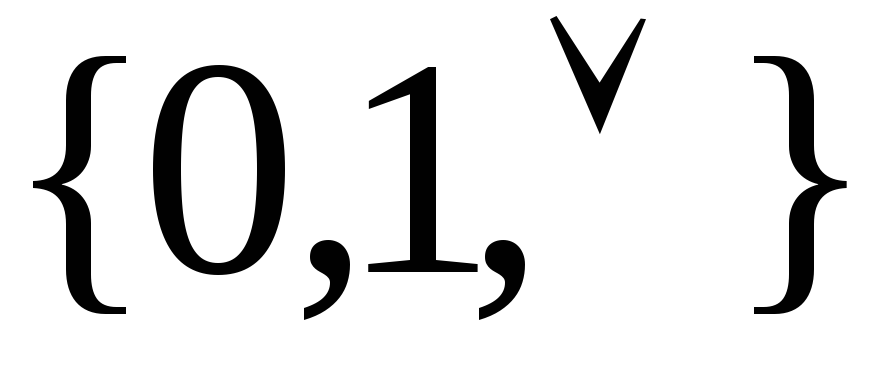, а функции в замыкании нет, следовательно системане полна в классеМ следовательно начальная система 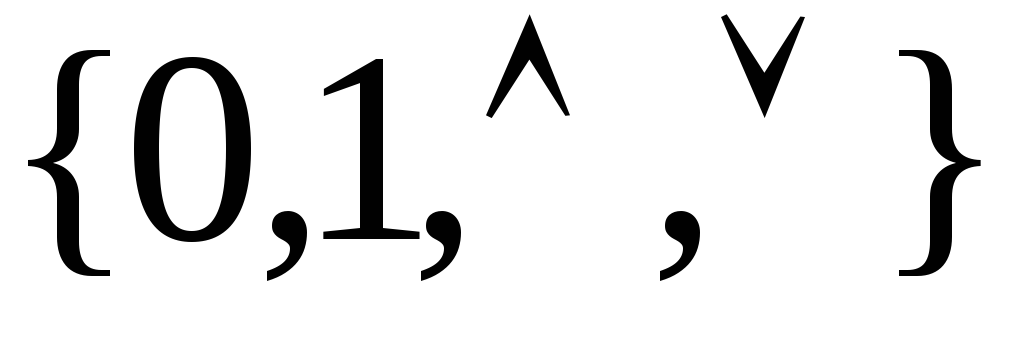есть базис в классе монотонных функций.

5) Система полна в классеL . Покажем, что все собственные подсистемы в классе линейных полными не являются:

следовательно начальная система является базисом в классе линейных функций.

Замечание

Вопросы о представлении функций в монотонном базисе потребуются в следующем разделе минимизации двоичных фукций.

Замечание

Пост нашел все замкнутые классы в классе двоичных функций и описал структуру их взаимных вложений.