
- •2. Жидкости, их виды и свойства.
- •3. Течение жидкости, ее количественная оценка.
- •4. Ламинарное и турбулентное течение и их характеристики.
- •Число рейнольдса.
- •6. Внутренне трение ( вязкость) и факторы её опредляющие. Уравнение ньютона. Виды вязкости и их характеристика.
- •7. Коэффициенты абсолютной и относительной вязкости.
- •8. Закон гагена – пуазейля и следствия из него.
- •9. Ньютоновские и неньютоновские жидкости, их виды и характеристика.
- •Ньютоновские жидкости
6. Внутренне трение ( вязкость) и факторы её опредляющие. Уравнение ньютона. Виды вязкости и их характеристика.
Внутренним трением (вязкостью) – называется свойство сред оказывать сопротивление при перемещении их частиц относительно друг друга под действием внешней силы.
Вязкость обусловлена силами межмолекулярного взаимодействия.
Опыт: поместим слой жидкости между двумя параллельными твердыми пластинами на расстоянии X . Нижняя пластина закреплена.

 F
F

 1
1
 2
2

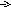 3
3

 X
4
X
4




Если потянуть за верхнюю пластину силой F, то она приобретает скоростьV1, и с такой же скоростью двигается самый верхний слой жидкости, прилегающий к пластине.
Этот слой влияет на лежащий под ним слой жидкости и заставляет его двигаться со



скоростью V2 (причем V2<V1) и т.д.
Каждый слой ускоряет нижележащий, но замедляет вышележащий. Слой «прилипший» к нижней пластине, неподвижен. Силы, действующие между слоями и направленные по касательной к поверхности слоев, называются
силами внутреннего трения (вязкости).
У читывая
расстояние «∆Х» между двумя пластинами,
Ньютон установил, что силы вязкости
пропорциональны площади взаимодействующих
слоев «S»
и будут тем больше, чем больше отношение
разности скоростей ∆V
к расстоянию между слоями «∆Х».
читывая
расстояние «∆Х» между двумя пластинами,
Ньютон установил, что силы вязкости
пропорциональны площади взаимодействующих
слоев «S»
и будут тем больше, чем больше отношение
разности скоростей ∆V
к расстоянию между слоями «∆Х».

 F~S
F~
∆/
∆X·S
F~S
F~
∆/
∆X·S
F~ ∆/ ∆X
F=·![]()
![]() x·S
x·S
Т.о. уравнения Ньютона.
“”коэффициент абсолютной (динамической) вязкости
Если поделить на “S”, то:
F/S=·![]()
![]() X
X
F/S= м² - напряжение сдвига,
![]() /
/![]() =
=
![]()
- скорость сдвига.
- скорость сдвига.
Т
=·
реологическая форма уравнения Ньютона
7. Коэффициенты абсолютной и относительной вязкости.
1. “”- абсолютная (динамическая) вязкость.
= [Пас]
Этот коэффициент зависит от состояния жидкости и от силы межмолекулярного взаимодействия.
При t0 = 360 С воды =1·10 -³ [Пас]
При t0 = 360 С крови=4·10 -³ [Па·с]
2. « » - относительная вязкость.
жидкводы
- безразмерная величина
8. Закон гагена – пуазейля и следствия из него.
В 1839 г. Гаген, а затем в 1841 г. Пуазейль независимо друг от друга установили, что объемный расход ламинарно текущей жидкости (Q=V/t) прямо пропорционален разности давлений на концах трубки тока и радиусу этой трубки в «4-ой» степени и обратно пропорционален длине трубки и коэффициенту динамической вязкости.
Q=(/8)(∆
p·![]() )/ l·
)/ l·![]() /l·
- закон
Гагена-Пуазейля.
/l·
- закон
Гагена-Пуазейля.
Следствия:
!
10
Т.к Q~![]() , то при незначительном уменьшении
радиуса трубки , будет значительно
уменьшаться количество жидкости,
прошедшей через сечение.
, то при незначительном уменьшении
радиуса трубки , будет значительно
уменьшаться количество жидкости,
прошедшей через сечение.
 !
20 Линейная
скорость течения жидкости «
» будет прямопропорциональна квадрату
радиуса трубки « r²
».
!
20 Линейная
скорость течения жидкости «
» будет прямопропорциональна квадрату
радиуса трубки « r²
».


Q
=
∆p·r²/8··l![]() )
/·l
V/t=(/8)·(∆
p·
)
/·l
V/t=(/8)·(∆
p·![]() /·l)
/·l)
Q
 =V/t
S·l/t=(/8)(
∆p·
=V/t
S·l/t=(/8)(
∆p·![]() /·l)
/·l)
V=S·l
·r²=(/8)(∆p·![]() /·l)
/·l)
S=r²
30 Время прохождения равных объемов жидкостей через трубки одинакового сечения тем больше, чем больше вязкость жидкости.
V/t1=(/8)·(
∆p·![]() )/l·1
V/t2=(/8)·(
∆p·
)/l·1
V/t2=(/8)·(
∆p·![]() )/l·2
)/l·2
η1/t1=(π/8)·(
∆p·![]() /)l·V
η2/t2=(π/8)·(
∆p·
/)l·V
η2/t2=(π/8)·(
∆p·![]() )/l·V
)/l·V

t1/t2=η1/η2

40 Расстояния, пройденные одинаковыми объемами разных жидкостей по трубкам одного сечения обратно пропорциональны их вязкости.
V/t=(π/8)·(
∆p·![]() )/l1·η1
V/t=(π/8)·(
∆p·
)/l1·η1
V/t=(π/8)·(
∆p·![]() )/l2·η2
)/l2·η2
l1·η1=(π/8)·(
∆p·![]() ·t)/V
l2·η2=(π/8)·(
∆p·
·t)/V
l2·η2=(π/8)·(
∆p·![]() ·t)/V
·t)/V
l1/l2=η2/η1
l1·η1=l2·η2
