
- •Комплект
- •Индивидуальных заданий
- •По дисциплине «Математика»
- •Для первого курса технических специальностей
- •1 Семестр
- •Выполнение действий над действительными числами
- •Нахождение приближенных значений величин и погрешностей вычислений
- •Выполнение действий над комплексными числами
- •Нахождение значений корней и степеней
- •Преобразование степенных и показательных выражений
- •Решение рациональных уравнений и неравенств
- •Решение иррациональных уравнений и неравенств
- •Вычисление значений логарифмов
- •Преобразование логарифмических выражений
- •Решение показательных уравнений и неравенств
- •Решение логарифмических уравнений и неравенств
- •Нахождение углов и расстояний в пространстве
- •Нахождение двугранных углов
- •Изображение пространственных фигур
- •Нахождение числа перестановок, размещений, сочетаний
- •Решение комбинаторных задач
- •Выполнение действий над координатами
- •Выполнение действий над векторами
- •Измерения углов
- •Вычисление значений тригонометрических функций
- •Решение треугольников
- •Преобразования тригонометрических выражений
- •Решение тригонометрических уравнений
Нахождение двугранных углов
|
|
1 |
2 |
3 |
|
|
Решите задачу |
Решите задачу |
Решите задачу |
|
* |
Основание пирамиды SABC– прямоугольный треугольник с прямым угломB,SO– высота пирамиды. Построить ЛУДУ при ребрахABиBC. |
Через вершину квадрата АВСDпроведён к его плоскости перпендикулярDМ равный 10см. Угол между плоскостями АВС иMDCравен 45º. Найти площадь треугольника ВСM |
Через вершину Dтупого угла ромба АВСDпроведен перпендикулярDKравный 9 см. Диагонали ромба равны 12 см и 16 см. Вычислить углы между плоскостями АВС иKВС |
|
1 |
Основание пирамиды MNPK-прямоугольный треугольникNPKс прямым углом К. Высота МО падает в центр описанной окружности. Постройте ЛУДУ при ребрахNKиPK. |
Отрезки АС и ВС, лежащие в гранях прямого двугранного угла перпендикулярны к его ребру. Вычислите расстояние между точками А и В, если АС=10 см, ВС=24 см |
Дан треугольник MNP, у которого угол М равен 90º;MN=9 см. Через сторону РМ проведена плоскость α под углом 60º к плоскости треугольникаMNP. Найти расстояние от вершиныN до плоскости α. |
|
2 |
Основанием пирамиды SABCDявляется квадрат. ВысотаSOпадает в точку пересечения диагоналей. Построить ЛУДУ при ребрах АВ и ВС. |
Точка К, лежащая в грани
двугранного угла удалена от другой
грани на 12 см, а от ребра на 8 |
Катет прямоугольного треугольника APNс прямым угломNлежит в плоскости α, а угол между плоскостями α иAPNравен 60º. Найти расстояние от точки Р до плоскости α, еслиAN=12 см , АР=13 см. |
|
3 |
Основание пирамиды SABC– треугольник, у которогоAB=BC, высотой служит реброSB. Построить линейный угол двугранного угла при ребреAC. |
В грани двугранного угла равного 30º расположена точка A. Вычислить расстояние от точкиAдо второй грани, если она удалена от ребра двугранного угла на 16 см. |
Правильные треугольники ABCиDBCрасположены так, что вершинаDпроектируется в центр треугольникаABC. Найти угол между плоскостями этих треугольников. |
|
4 |
Основание пирамиды SABC– прямоугольный треугольник с прямым угломABC,SO– высота пирамиды. Построить линейные углы двугранных углов при ребрахABиBC. |
Угол между плоскостями α и β равен 60º. Точка С принадлежит ребру этого угла, отрезки АС и ВС перпендикулярны этому ребру и равны соответственно 5 см и 8 см. Вычислить расстояние между концами этих перпендикуляров. |
Через сторону ABтреугольникаABCпроведена плоскость α , расстояние от вершиныCдо плоскости α равно 7,5 см. Найти угол между плоскостью α и плоскостью треугольника, еслиAB=16 см.,AC=BC=17 см. |
|
|
1 |
2 |
3 |
|
5 |
Основание пирамиды SABCправильный треугольник,SO-высота. Постройте линейные углы двугранных углов при ребрах основании пирамиды. |
Внутри прямого двугранного угла взята точка А, удаленная от его граней на 12 см и 16 см. Вычислите расстояние от точки А до ребра двугранного угла. |
Двугранный угол между
плоскостями треугольников MNPиMNKравен 60º. Найти РК,
если МК=NK=5см,MN=6см,MP=NP=3 |
|
6 |
Основанием пирамиды является прямоугольник. АВСD. ВысотаSOпадает в точку пересечения диагоналей. Постройте ЛУДУ при ребрахBC иCD. |
На ребре двугранного угла, равного 180º расположена точка А. В его гранях проведены перпендикуляры к ребру АВ и ВС, равные соответственно 10 см и 8 см . Найти расстояние между точками В и С. |
Точка К удалена от каждой стороны равностороннего треугольника АВС на 8 см; АВ=24 см. Найти величину двугранного угла с ребром ВС, грани которого содержат точки К и А. |
|
7 |
Основание пирамиды SABCD-равнобедренная трапеция, у которой АD//ВС. Величина пирамиды проецируется в середину ребра АД. Построить ЛУДУ при ребре ВС. |
Через вершину квадрата АВСД проведён к его плоскости перпендикуляр РК равный 10см. Угол между плоскостями АВС и RDCравен 45 . Найти площадь треугольника ВСК |
Сторона (АВ) квадрата АВСД лежит в плоскости. Прямая СД удалена от этой плоскости на 18см. ВС=36см.Вычислите угол между плоскостью квадрата и плоскостью |
|
8 |
Основание пирамиды SАВС прямоугольный треугольник АВС с прямым углом С. ВысотаSо падает в центр описанной окружности. Построить линейные углы двугранных углов при рёбрах АС и ВС |
Через вершину острого угла прямоугольного треугольника АВС проведён перпендикуляр АД к его плоскости. АД=6см; АСВ=90; АВС=30. Угол между плоскостями DCLи АВС равен 60. Найти длины ДС и ДВ. |
Через центр О квадрата АВСД проведён к его плоскости перпендикуляр КО угол между прямой КС и плоскостью квадрата равен 60 . АВ=18см,.Найти угол между плоскостями АКС и ОКВ. |
|
9 |
Основание пирамиды SАВСД - квадрат. ВысотаSО падает в центр вписанной в квадрат окружности . Построить линейные углы двугранных углов при рёбрах основания пирамиды. |
Через вершину квадрата ABCDпроведен перпендикулярDK= 10 см. Угол между плоскостямиABCиKBCравен 45º. Найти площадь квадрата. |
Стороны АС правильного треугольника АВС лежит в плоскости α. Угол между плоскостями треугольника 4α равен 60º; АС=12 см. Найти расстояние от точки в до плоскости α. |
|
10 |
Основание пирамиды АВСД- прямоугольник АВСД; высота SА. Построить линейные углы двугранных углов при рёбрах АВ и АС |
Угол между плоскостями α и β равен 60º точка А, лежащая в плоскости α удалена от β на 12 см. Найти расстояние от точки А до линии пересечения. |
Через вершину Dтупого угла ромба АВСDпроведен перпендикулярDMравный 9,6 см. Диагонали ромба равны 12 см и 16 см. Вычислить углы между плоскостями АВС и МВС |

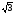 см. вычислите величину двугранного
угла.
см. вычислите величину двугранного
угла.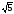 см.
см.