
- •Министерство образования и науки российской федерации
- •Раздел I. Теория вероятностей
- •Тема 1. Случайные события
- •1.1 Классификация событий
- •1.2. Вероятность событий
- •Свойства вероятности
- •1.3. Элементы комбинаторики
- •1.4. Операции над событиями
- •Тема 2. Основные теоремы
- •2.1. Теорема сложения вероятностей несовместных событий
- •2.2. Теорема умножения вероятностей
- •2.3. Формула полной вероятности. Формулы Байеса
- •Тема 3. Повторные независимые испытания
- •3.1. Формула Бернулли
- •3.2. Формула Пуассона
- •3.3. Локальная теорема Муавра-Лапласа
- •Свойста функци , ее график
- •3.4. Интегральная теорема Муавра-Лапласа
- •Свойства функции :
- •Тема 4. Дискретная случайная величина и её характеристики
- •4.1. Понятие случайной величины
- •4.2. Закон распределения дискретной случайной величины
- •4.3. Математические операции над случайными величинами
- •4.4. Числовые характеристики дискретной случайной величины
- •Свойства
- •Свойства
- •4.5. Биноминальный закон распределения и закон Пуассона
- •4.6. Функция распределения случайной величины
- •Свойства функции распределения
- •Тема 5. Непрерывные случайные величины.
- •5.1. Плотность распределения вероятностей непрерывных случайных величин
- •Свойства плотности распределения
- •5.2. Числовые характеристики непрерывных случайных величин
- •5.3. Нормальный закон распределения
- •Свойства случайной величины, распределенной по нормальному закону
- •5.4. Центральная предельная теорема. Теорема Ляпунова
- •Тема 6. Двумерные (n-мерные) случайные величины
- •6.1. Способы задания двумерной случайной величины
- •Свойства двумерной функции распределения
- •6.2. Условные законы распределения
- •6.3. Ковариация и коэффициент корреляции
- •Свойства коэффициента корреляции
- •6.4. Двумерный нормальный закон распределения
- •Тема 7. Закон больших чисел
- •Неравенство Маркова (лемма Чебышева)
- •Неравенство Чебышева
- •Теорема Чебышева
- •Раздел II. Математическая статистика Тема 8. Выборочный метод. Общие вопросы
- •8.1. Понятие о вариационных рядах
- •8.2. Эмпирическая функция распределения
- •Свойства :
- •8.3. Числовые характеристики вариационного ряда
- •Основные свойства
- •Основные свойства дисперсии
- •Упрощённый способ расчёта средней арифметической и дисперсии
- •8.4. Выборочный метод
- •Тема 9. Оценка доли признака и генеральной средней
- •Точечные оценки генеральной совокупности. Свойства оценок
- •Интервальная оценка параметров
- •Доверительный интервал для генеральной средней и генеральной доли по большим выборкам
- •Объём выборки
- •Тема 10. Статистическая проверка гипотез
- •10.1. Статистическая гипотеза и общая схема её проверки
- •1) - То нулевую гипотезуотвергают,
- •2) - То нет оснований отвергнуть.
- •10.2. Построение теоретического закона распределения по опытным данным. Критерий согласия Пирсона
- •Правило проверки нулевой гипотезы
- •Тема 11. Корреляция и регрессия
- •11.1. Линейная парная регрессия
- •11.2. Оценка тесноты корреляционной зависимости
- •Свойства выборочного коэффициента корреляции r
- •Проверка значимости выборочного коэффициента корреляции
4.2. Закон распределения дискретной случайной величины
Определение. Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Закон распределения дискретной случайной величины Х (д.с.в. Х ) удобно задавать в виде таблицы, первая строка которой содержит возможные значения Х , а вторая – соответствующие им вероятности.
|
Х |
х1 |
х2 |
… |
хn |
|
Р |
p1 |
p2 |
… |
pn |
Такая таблица называется рядом распределения д.с.в. Х.
Так как в одном
испытании случайная величина принимает
только одно возможное значение, то
события
![]() образуют полную группу. Следовательно,
сумма вероятностей этих событий равна
единице:
образуют полную группу. Следовательно,
сумма вероятностей этих событий равна
единице:![]() .
.
Ряд распределения можно изобразить графически: по оси абсцисс откладывают значения случайной величины, а по оси ординат – соответствующие им вероятности. Соединяя полученные точки, получим ломаную, которая называется многоугольником распределения (рис. 4.1).

Пример 4.1.Вероятности того, что студент сдаст экзамены по математике и физике равны 0,8 и 0,9, соответственно. Составить закон распределения числа экзаменов, которые сдаст студент.
Решение. Пусть
![]() - число сданных экзаменов. Возможными
значениями д.с.в.Х
являются числа
- число сданных экзаменов. Возможными
значениями д.с.в.Х
являются числа
![]() .
Соответствующие им вероятности найдем
воспользовавшись правилом умножения
вероятностей:
.
Соответствующие им вероятности найдем
воспользовавшись правилом умножения
вероятностей:
![]() ,
,
![]() ,
,
![]() .
.
Т.о. ряд распределения с.в. Х имеет вид
|
Х |
0 |
1 |
2 |
|
Р |
0,02 |
0,26 |
0,72 |
Контроль:
![]() .
.
4.3. Математические операции над случайными величинами
Пусть д.с.в. Х задана в виде ряда распределения
|
Х |
х1 |
х2 |
… |
хn |
|
Р |
p1 |
p2 |
… |
pn |
Произведениемслучайной величины
 на постоянную величину
на постоянную величину называется случайная величина
называется случайная величина ,
которая принимает значения
,
которая принимает значения с теми же вероятностями
с теми же вероятностями .
.m - й степеньюслучайной величины
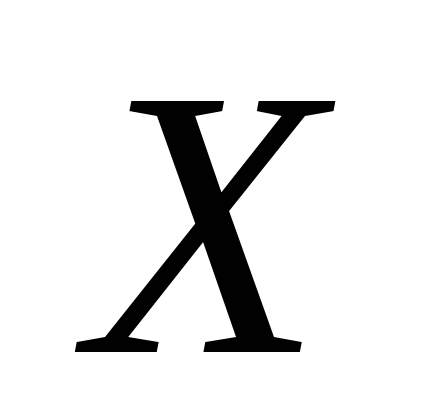 ,
то есть
,
то есть называется случайная величина, которая
принимает значения
называется случайная величина, которая
принимает значения с теми же вероятностями
с теми же вероятностями .
.
Пример 4.2.Задана случайная величинаХ
|
|
-2 |
1 |
2 |
|
|
0,5 |
0,2 |
0,3 |
Найти закон
распределения случайных величин а)
![]() ,
б)
,
б)![]() .
.
Решение.
а)Возможные
значения с.в.![]() таковы:
таковы:![]() .
.
Вероятности этих значений равны вероятностям соответствующих значений с.в.Х.
|
|
-6 |
3 |
6 |
|
|
0,5 |
0,2 |
0,3 |
б)Возможные
значения с.в.Z таковы:![]() .
.
При этом
![]() .
.
|
|
1 |
4 |
|
|
0,2 |
0,8 |
3) Суммой (разностьюилипроизведением)случайных величин![]() и
и![]() называется случайная величина, которая
принимает все возможные значения вида
называется случайная величина, которая
принимает все возможные значения вида![]() (
(![]() ,
,![]() )
с вероятностями
)
с вероятностями![]() того, что случайная величина
того, что случайная величина![]() примет значение
примет значение![]() ,
а
,
а![]() - значение
- значение![]() :
:
![]() ,
,
где
![]() ,
,![]() .
.
Пример 4.3.Заданы
законы распределения случайных величин![]() и
и![]() :
:
|
|
0 |
1 |
|
|
0,2 |
0,8 |
|
|
-1 |
0 |
1 |
|
|
0,3 |
0,5 |
0,2 |
Найти закон
распределения с.в.![]() .
.
Решение. Найдем возможные значения с.в.С:
-1 = 0 + (-1); 0 = 0 + 0; 1 = 0 + 1; 0 = 1 + (-1); 1 = 1 + 0; 2 = 1 + 1, т.е.
с.в.Спринимает
значения:![]() .
.
Находим вероятности этих значений:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
|
|
-1 |
0 |
1 |
2 |
|
|
0,06 |
0,34 |
0,44 |
0,16 |
