Свойства вероятности

1. Вероятность любого события заключена между нулем и единицей

.

2. Вероятность достоверного события равна единице.

3. Вероятность невозможного события равна нулю.

Действительно,

1. Т.к., то разделив обе части неравенства наn, получим 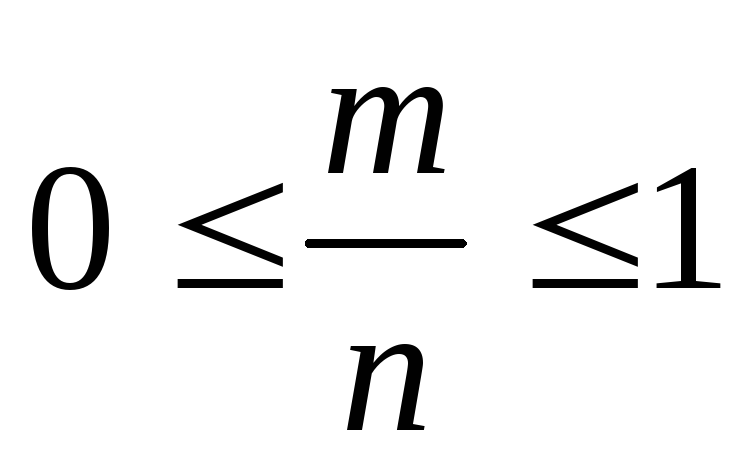. Следовательно,.

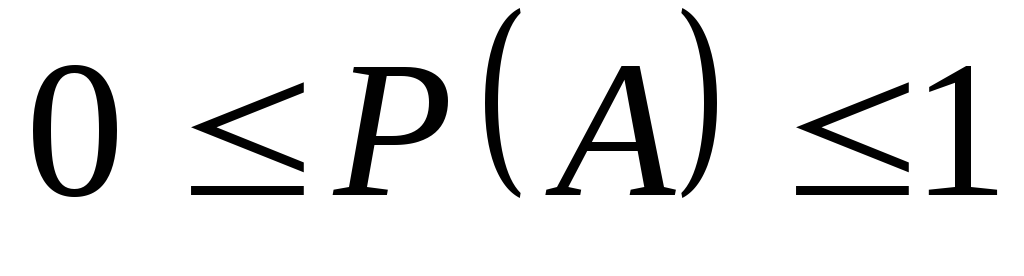2. Если событие достоверное, то 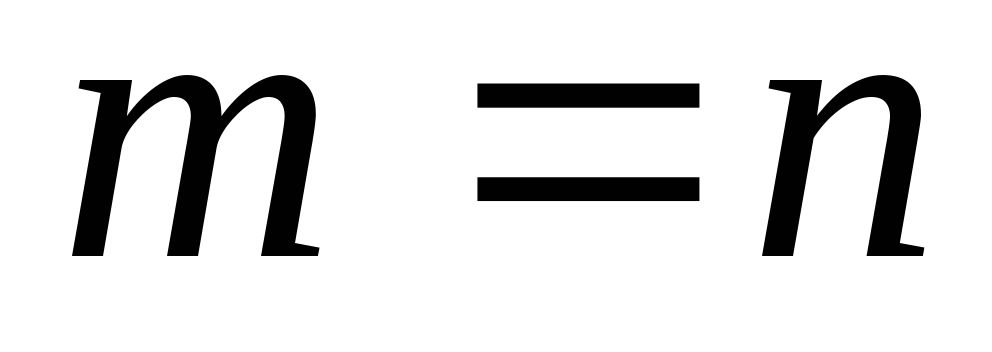. Следовательно,.

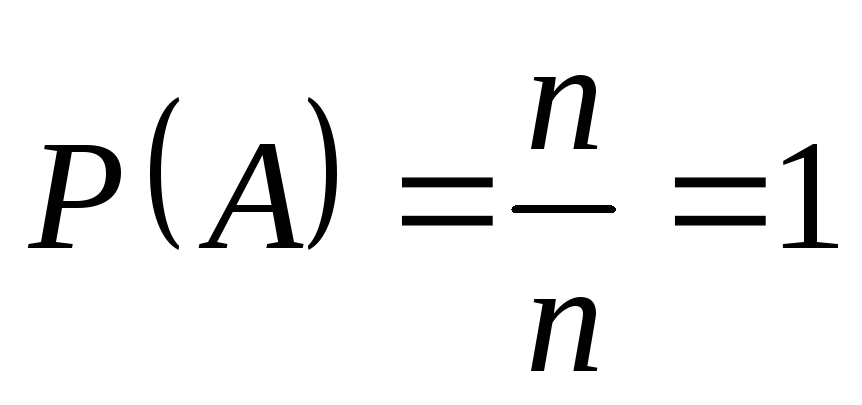3. Если событие невозможное, то 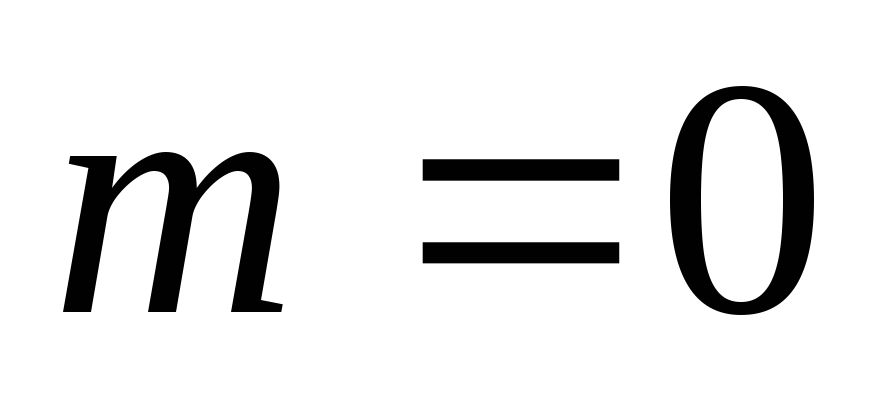. Следовательно,.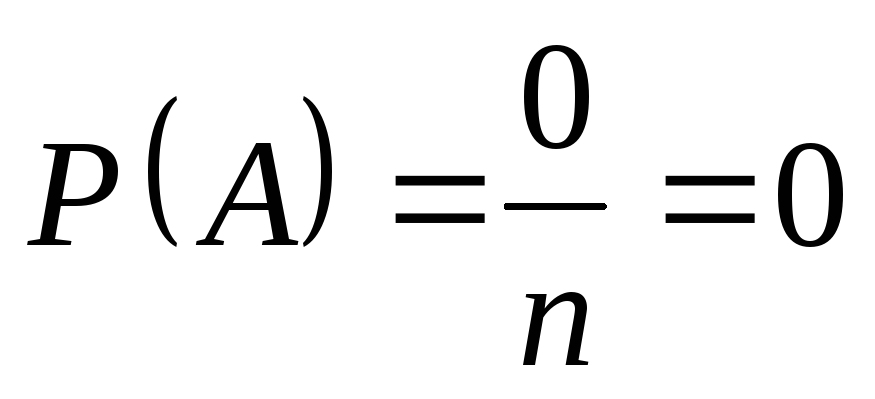

Определение. Пусть проведено испытаний, в которых событиеосуществилосьраз. Тогдаотносительной частотой события называется отношение числа испытаний, в которых осуществилось событие, к общему числу всех испытаний

.

Многочисленные наблюдения показали, что если в одинаковых условиях производят опыты, в каждом из которых число испытаний достаточно велико, то относительная частота в различных опытах колеблется около некоторого постоянного числа, которое и является вероятностью события.

Определение. Статистической вероятностью называют относительную частоту события или число, близкое к ней.

Все свойства классической вероятности сохраняются и для статистической вероятности.

1.3. Элементы комбинаторики

Для вычисления вероятности события необходимо уметь рассчитывать число различных комбинаций, т.е. уметь определять значения и.

Определение. Размещением из различных элементов поэлементов называется соединение, которое отличается либо составом, либо порядком своих элементов.

Число размещений обозначается символом и вычисляется по формуле

,

где , причем 1! = 1, 0! = 1.

Пример 1.2. Сколько трехзначных чисел с неповторяющимися цифрами можно составить из цифр 1,2,3…9?.

Решение. Каждое трехзначное число является размещением из девяти цифр по три. Их число равно.

Определение. Сочетаниями из элементов поэлементов называются соединения, которые различаются только составом своих элементов.

Число сочетанийобозначается символом и вычисляется по формуле

.

Пример 1.3. Сколькими способами можно выбрать 2 детали из ящика, содержащего 10 деталей?

Решение. Т.к. порядок выбора деталей неважен, то взять 2 детали из имеющихся десяти можно способами.

Определение. Перестановками из элементов называются всевозможные соединения из этихэлементов.

Число перестановок обозначается символом и вычисляется по формуле

.

Пример 1.4. В конкурсе выступают 7 участников. Порядок их выступления определяется жребием. Сколько различных вариантов жеребьёвки при этом возможно? Решение. Каждый вариант жеребьёвки отличается только порядком участников конкурса, т.е. является перестановкой .

1.4. Операции над событиями

Определение. Суммой нескольких событий называется событие, состоящее в наступлении хотя бы одного из данных событий.

Если события и несовместные, то их суммаобозначает наступление или событияили события.

Определение. Произведением нескольких событий называется событие, состоящее в совместном наступлении всех этих событий.

Если и совместные события, то их произведениеозначает наступление и событияи события.

Тема 2. Основные теоремы

2.1. Теорема сложения вероятностей несовместных событий

Теорема. Вероятность суммы несовместных событий равна сумме вероятностей этих событий

.

В частности .

Доказательство рассмотрим на примере суммы 2-х событий и .

Пусть - общее число возможных исходов некоторого испытания;- число исходов, благоприятствующих событию;- число исходов, благоприятствующих событию. Тогда- число исходов, благоприятствующих наступлению либо события, либо события, т.е. события.

Следовательно, .

Следствие 1. Сумма вероятностей событий, образующих полную группу, равна единице.

Если А, В,…, К образуют полную группу, то .

Следствие 2. Сумма вероятностей противоположных событий равна единице

или .

Пример 2.1. В ящике 30 шаров: 10 красных, 5 синих, 15 белых. Найти вероятность появления цветного шара.

Решение. Пусть событие С = {появление цветного шара}.Появление цветного шара означает появление либо красного шара (событие), либо синего шара (событие).,. Т.к. событияи несовместные, то

.

Пример 2.2. Вероятность того, что день будет пасмурным равна . Найти вероятность того, что день будет ясным.

Решение. События день дождливый () и день ясный () – противоположные. Следовательно, ,.