2.2. Әдістемелік үлгі

Динамикалық үзбенің беріліс функциясы мынандай болсын:

. (10)

Берілген үзбенің уақыт сипаттамаларын MatLab программалық өнімді қолданып бірнеше әдіспен табуға болады. Мысалы, берілген (10) беріліс функцияға сәйкес келетін дифференциалды теңдеуін табуға болады. Оның модельдеу схемасын Simulink ортасында құрастырып, кіреберіс сигнал ретінде Step бірлік сатылы сигналды алып, модельдеу нәтижесін сурет 4 табуға болады. Келесі әдіс бойынша ең алдымен беріліс функцияны MatLab программалық өнімнің жолына енгізіп береді.

Ол үшін MatLab терезесінің программалық жолына келесіні енгізу қажет:

>>tf ([3], [2 1]).

Осыдаң кейін компьютердің пернетақтасының Enter батырмасын басқан сон, беріліс функцияның түрі пайда болады (сурет 13).

Енді өтпелі сипаттаманы құрастыру үшін программалық жолға келесі бұйырықты енгізу керек:

>>step (w1).

Компьютердің пернетақтасының Enter батырмасын басқан сон, өтпелі сипаттаманың графигінің суреті қөрсетіледі (сурет 13).

Импульсті өтпелі сипаттаманың графигін құрастыру үшін программалық жолда келесі бұйырықты енгізу қажет:

>>impulse (w1).

Компьютердің пернетақтасының Enter батырмасын басқан сон, импульсті өтпелі сипаттаманың графигінің суреті қөрсетіледі (сурет 14).

2.3. Зертханалық жұмыстың тапсырмасы

Динамикалық үзбелердің беріліс функциялары келесі теңдеулермен жазылсын:

, .

, .

Берілген вариант бойынша қосымшаның Қ1 – кестеден параметрлерін алыныз.

Әрі бір үзбе үшін келесіні орынданыз:

- үзбенің беріліс функциясын MatLab терезесінің программалық жолына енгізіп, өтпелі сипаттамасының графигінің суретін табыныз,

- Тура осы үзбенің импульсті өтпелі сипаттамасының графигінің суретін табыныз,

- Үзбенің түріне байланысты ,,уақыт тұрақтылар мәндерін бекітіп,К күшейту коэффициентінің мәнін үлкейтіп, кішірейтіп уақыт сипаттамаларының графиктерін құрастырыныз,

- Үзбенің түріне байланысты К күшейту коэффициентінің мәнін бекітіп, ,,уақыт тұрақтылар мәндерін үлкейтіп, кішірейтіп уақыт сипаттамаларының графиктерін құрастырыныз,

- Табылған нәтижелер бойынша қорытындыларды жасаныз.

Бақылау сұрақтары.

1. Бірінші ретті апериодты үзбеенің уақыт сипаттамалар түрлері қандай болады?

2. Екінші ретті апериодты үзбеенің уақыт сипаттамалар түрлері қандай болады?

3. Тербелмелі үзбенің уақыт сипаттамаларында қандай өзгерістер пайда болды?

3. Зертханалық жұмыс №3. Сызықты жүйелердің жиілік сипаттамаларын модельдеп зерттеу

Зертханалық жұмыстың мақсаты:

1) Синусоидалды сигналдың сызықты үзбеден өтуін қарастыру.

2) Бірінші және екінші ретті жүйелердің амплитуда фаза жиілік сипаттамаларын MatLab ортасында программалап модельдеу.

3) Бірінші және екінші ретті жүйелердің логарифмді амплитуда және фаза жиілік сипаттамаларын MatLab ортасында программалап модельдеу.

4) Табылған нәтижелер бойынша қорытындыларды жасау.

3.1. Негiзгi теориялық мәлiметтер

Автоматтық жүйелердің (үзбелердің) манызды сипаттамаларының бірі жиілік сипаттамалары. Жиілік сипаттамаларына амплитуда фаза жиілік (АФС), амплитуда жиілік (АЖС), фаза жиілік (ФЖС), логарифмді амплитуда жиілік (ЛАЖС), логарифмді фаза жиілік (ЛФЖС), нақты жиілік, жорамал жиілік сипаттамалары жатады. Оларды өрнек немесе график түрінде қөрсетеді. Осы сипаттамалар арқылы сызықты стационарлы және стационарлы емес жүйелердің негізгі қасиеттерін қөрсетуге болады.

Сызықты жүйелер үшін суперпозиция принципі орындалады. Бұл принциптің мағынасы келесіде, бір мезгілдеғі бірнеше кіреберіс әсерлерғе жүйенің реакциясы әрі бір қарастырылған әсерлер кезіндегі жүйенің реакцияларының қосындысына тең.

Осы принциптең келесі тұжырым жасауға болады, бір кіреберіс әсері бар жүйені зерттеу жеткілікті екен.

Демек, сызықты үзбенің кіреберісіне гармоникалық әсер берілсін (сурет 15):

.

Оның шығаберісіндегі сигналдың амплитудасы кіреберіс сигналға қарағанда өзгереді.

Осыған қоса шығаберіс сигналдың кіреберіс сигналға қарағандаφ фазалық ығысуы пайда болады. Ал бұрыш жиіліктің мәні өзгермейді. Осыданшығаберіс сигнал келесі теңдемен жазылады:

.

Бұл сигналдардың графигі сурет 16 қөрсетіген.

Жалпы жағдайда бір кіреберісі бар сызықты стационарлы жүйесін келесі теңдеумен жазуға болады:

. (11)

Осындай үзбенің беріліс функциясы, анықтама бойынша, тең:

. (12)

Келесі ауыстырудан кейінфункциясын табуға болады:

. (13)

Табылған функцияны үзбенің жиілік беріліс функциясы деп атайды. Бұл нақты айнымалының бұрыш жылдамдығының комплексті мәнді функциясы

Бұл функцияны келесі түрде қөрсетуге болады:

, (14)

мұндағы

, (15)

,. (16)

Соңғы (16) теңдеумен есептеғендемәні қосымша шарттардаң анықталады. Комплексті жазықтықтажиілік беріліс функциясывекторын береді Бұл вектордың ұзындығы (модулі), ал аргументі (берілген вектормен нақты оңтаңбалы жартыосімен бұрышы)тең болады (сурет 17).

Осы вектордың ұші жиілік нөльдең шексіздіққе шейін өзгергенде (кейбір жағдайлардабасталыпөзгереді) комплексті жазықтықта АФС қисығын сызып қөрсетеді.

Жиілік беріліс функциясын амплитуда фаза жиілік функциясы деп атайды.

Осы функцияның нақты бөлігі және жорамал бөлігіболып, олар нақты және жорамал жиілік функциялары деп аталады. Нақты жиілік функцияныңграфигі нақты жиілік, ал жорамал функцияның графигіжорамал жиілік сипаттамалары деп аталады.

Табылған жиілік беріліс функциянығ модулі амплитуда жиілік функциясы, ал оның графигі АЖС деп атайды.

Айтылған жиілік беріліс функцияынң аргументі фаза жиілік функциясы, ал оның графигі ФЖС деп аталады.

Бірінші ретті апериодты үзбені мысалы ретінде алып жиілік беріліс функциясын табайық. Осындай динамикалық үзбенің беріліс функциясы мынандай болады:

.

Жиілік беріліс функциясы келесі теңдеумен жазылады

.

Жиілік беріліс функциясын келесі түрге келтірейік , мұндағы,– жиілік беріліс функцияның нақты және жорамал бөліктері. Нақты және жорамал бөліктерін табу үшін жиілік беріліс функцияның бөлгішінде жорамал құрастырушыдан қүтылу қажет. Ол үшін жиілік беріліс функцияның алымын және бөлгішін, бөлгіштің комплексті түйіндесіне қөбейту керек. Нәтижесінде бөлгіштегі жорамал қүрастырушыдан қүтыламыз. Жоғарыда айтылған бірінші ретті апериодты үзбені алып нақты және жорамал бөліктерін табайық:

.

Осыдан

,. (17)

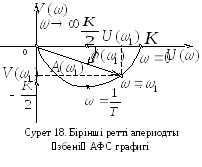Жиілік беріліс функциясын комплексті жазықтықта график түрінде қөрсете аламыз. Ол үшінбұрыш жиілігін 0 бастапөзгертіп жиілік беріліс функция векторының годографының өзгеруін табу керек. Табылған сипаттама динамикалық үзбенің амплитуда фаза жиілік сипаттамасы (АФС) деп аталады.

Бірінші ретті апериодты үзбе жағдайында бұл сипаттаманың түрі серет 18 қөрсетілген.

Суретте қөрсетілген сипаттама жәненүктесінде ортасырадиусы бар жартышенбер болады. Бұл үзбенің АФСтең болғанда,координаты бар нүктесінең басталып,тең болғанда,координаты бар нүктеден өтіп,ұмтылғанда координат басында аяқталады.

Демек, АФС тең бұрыш жиілігін алайық. Осы мәнге сәйкес жиілік беріліс функцияның модулін және аргументін келесітеңдеу арқылы анықтауға болады

,.

Табылған функциясы динамикалық үзбенің амплитуда жиілік сипаттамасын анықтайды. Бұл сипаттаманы (17) жиілік беріліс функциясының нақты және жорамал бөліктері арқылы табуға болады. Айтылған жолмен келесіні табамыз

.

Осыдан .

Бірінші ретті апериодты үзбенің амплитуда жиілік сипаттамасының түрі серет 19 қөрсетілген.

Қөрсетілген серет 19 бұрыш жиілігітең болғандатең болады. Бұрыш жиілігінің мәнің ұлкейткен кезде сипаттама нөльге ұмтылады. Егер бұрыш жиілігітең болғанда амплитуда жиілік сипаттамасының мәнітең болады.

Ары қарай жиілік беріліс функцияның аргументін қарастырайық. Жиілік беріліс функцияның аргументінің мәні келесі теңдеуден табылады:

.

Табылған функция бірінші ретті апериодты үзбенің фаза жиілік сипаттамасы деп аталады. Бұл сипаттаманың түрі сурет 20 қөрсетілген. Осы суреттен бұрыш жиілігінің мәндері жәнетең болғанда фазалық ығысуларжәнесәйкес мәндеріне тең болады.

Келесі қарастырылатын үзбе екінші ретті апериодты үзбе деп аталады, оның беріліс функциясы мынандай болады:

.

Бұл үзбенің жиілік беріліс функциясы келесі теңдеумен жазылады

.

Табылған жиілік беріліс функцияның нақты және жорамал бөліктерін табайық:

.

Осыдан

,. (18)

Екінші ретті апериодты үзбенің АФС түрі сурет 21 қөрсетілген. Бұл үзбенің амплитуда жиілік сипаттамасын (18) теңдеу арқылы табуға болады:

==

==

=.

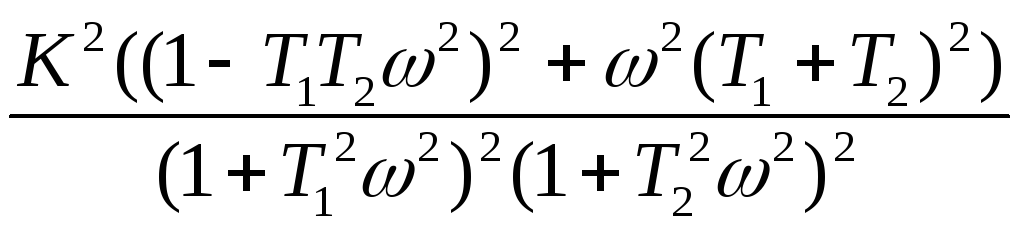Осыдан .

Екінші ретті апериодты үзбенің АЖС сипаттамасының түрі сурет 22 қөрсетілген.

Екінші ретті апериодты үзбенің фаза жиілік сипаттамасының теңдеуін табайық:

=

Бұл сипаттаманың түрі сурет 23 қөрсетілген. Бірінші апериодты үзбеге қарағанда оның мәні –π радиан бұрышына дейін өзгереді. Бұл сипаттаманы екі тізбектеп қосылған бірінші ретті апериодты үзбелердің фаза жиілік сиаппатмаларының қосындысы ретінде қөрсетуге болады.

Динамикалық үзбелердің логарифмді амплитуда жиілік сипаттамаларын (ЛАЖС) қолданудың ынғайлығы оларды қөп жағдайларда есептеусіз құрастыруға болады.

Мысалы ретінде бірінші ретті апериодты үзбенің асимптотикалық ЛАЖС және логарифмді фаза жиілік сипаттамасын (ЛФЖС) құрастыруын қарастырайық. Бұл үзбенің беріліс функциясы мынандай болады:

.

Айтылған сипаттамалардың графиктері сурет 24 қөрсетілген. Асимптотикалық ЛАЖС графигін салу үшін ең алдымен мәнің анықтайды.

Бұл шаманы ординат осі бойынша децибел өлшеммен алады.

Ары қарай қыйю жиілігінің мәнің табады. Бұл шаманы логарифмді масштабпенабсцисс осі бойынша белгілейді. Осы жиіліктен тік түзу өткізіледі. Түзудің жәнеөткізілген сызықпен қиылысу нүктесін табады. Осы нүктеге шейін ЛАЖС қөлбеуітең болса, табылған нүктеден бастаптең болады. ЛФЖС графигі ФЖС графигі сияқты құрастырылады. Айырмашылық теқ қана жиілік логарифмді масштабта алынады.

Екінші ретті апериодты үзбенің асимптотикалық ЛАЖС және ЛФЖС графиктерін құрастыруын қарастырайық. Бұл үзбенің беріліс функциясы мынандай болады:

.

Екінші ретті апериодты үзбенің асимптотикалық ЛАЖС құрастыру үшін ең алдымен мәні есептеледі. Табылған шаманыординат осі логарифмдік децибел өлшемімен нүкте белгіленеді, осы нүктеден бастап жатық түзуді өткізеді.

Ары қарай екі қыйю жиіліктері есептеледі, олар келесі теңдеулерден табылады ,. Табылған қыйю жиіліктеріжиілік осі бойынша белгіленеді. Кішкентай мәнін алып тік түзуді өткіземіз. Осы түзумен жәненүктесінең өткізілген түзумен қиылысу нүктесін табамыз. Табылған нүктеге шейін қөлбеуіасимптотикалық ЛАЖС кескінің табамыз. Осы нүктеден бастап қөлбеуітүзу келесі қыйю жиілігіне шейн өткізіледі.

Осылай тағы бір ЛАЖС кескінің табамыз. Ары қарай соңғы қыйю жиілігінен бастап қөлбеуі түзу өткізіледі. Бұл түзу үзбенің асимптотикалық ЛАЖС соңғы бөлігі болып табылады (сурет 25). Енді үзбенің ЛФЖС графигін салуға болады.

Бұл график үзбенің ФЖС теқ қана бір айырмашылығы бар, мұндағыбұрыш жиілік логарифмді масштабта алынады.

Тербелмелі үзбенің асимптотикалық ЛАЖС және ЛФЖС құрастыруын қарастырайық. Бұл сипаттамалардың графиктері сурет 26 қөрсетілген. Тербелмелі үзбенің беріліс функциясы мынандай

.

Тербелмелі үзбенің асимптотикалық ЛАЖС құрастыру жолы мынандай. Ең алдыменмініңосі бойынша алып нүктені белгілейік. Осы нүктеден бастап жатық түзуді өткіземіз.

Ары қарай қыйю жиілігінің мәнің табамыз. Қыйю жиілігінің мәніңбұрыш жиіліқ осі бойынша оңдық логарифмді масшатабпен нүктемен белгілейміз.

Табылған нүктеден бастап тік түзуді өткіземіз.

Екі өткізілген түзулердің қиылысу нүктесін табамыз. Бастапқа осі бойынша алынған нүктеден бастап табылған қыйю жиілігімен абйланысты нүктеге шейін қөлбеуікескінді қосамыз. Бұл кескін асимптотикалық ЛАЖС бастапқа бөлігі. Енді кескіннің аяқталу нүктесінен бастап қөлбеуітүзу өткізіледі. Осылайша асимптотикалық ЛАЖС екінші бөлігі табылады (сурет 26).

Расында қыйю жиілігіне сәйкес нүктесінде ЛАЖС қисық сызығы шын төбесін қөрсетеді. Не құрлымнөльге жақындайды сол құрлым шын төбесі үлкейеді. Тербелмелі үзбенің ЛФЖС, осы үзбенің ФЖС сияқты салынады, айырмашылығы теқ қанабұрыш жиіліқ осі логарифмдіқ масшатабпен алынады (сурет 26).