4.2 Әдістемелік ұсыныс.

Түйықталмаған жағдайдағы жүйенің беріліс функциясы келесі теңдеумен жазылсын

.

Келесі жәнетең болғанда,жәнешарттарды қанағаттандыратын тізбектеп қосылған қисындыратын құрылғыны таңдау қажет.

Ең алдымен теңестіріп, түйықталған жүйенің орнықтылығын зерттейік. Ол түйықталған жүйенің сипаттайтын теңдеуін табайық

.

Осыдан Гурвиц анықтаушы тең

,

онда түйықталған жүйе орнықты емес.

Есептеуді жүйенің өзгерілмейтін бөлігінің қалаулы ЛАЖС құрастыруынаң бастайды. Ол үшін жиілік тең болған жағдайдағы ордината мәнің табайық, қию жиіліктері тең,. Жүйеніңөзгерілмейтін бөлігінің ЛАЖС үш асимптотадан құрастырылады (сурет 20).

Ары қарай қалаулы ЛАЖС құрастырады. Жүйенің өзгерілмейтін бөлігінің астатикалығының реті және беріліс коэффицентінің мәндері қажетті талаптарға сәйкес келеді. Сол себептен қалаулы ЛАЖС төмен жиілік асимптотасы жүйенің өзгерілмейтін бөлігінің төмен жиілік асимптотасымен бірдей болады.

Берілген мәнге сәйкес сурет 18 номограмма бойынша табамыз

және.

Қалаулы ЛАЖС қию жиілігінің төмен шеқарасын табайық

.

Енді қию жиілігінің жоғары шеқарасын табайық

.

Осыдан деп таңдаймыз. Осы нүктеден қалаулы ЛАЖС орта жиілік асимптотасыненқеюмен өткіземіз (сурет 20). Осыдан кейін, сурет 19 номограмма бойыншатең болғандағыординатасыаралығында, фаза артықтығытең болу тиіс. Ординитасықылып түзуді өткізейік, қалаулы ЛАЖС орта жиілік асимптотасымен қиылысқан нүктеден, тексеру үшін арналған енқеюытең түйіндестіру асимптотасын өткізейік.

Демек, қалаулы ЛАЖС жоғары жиілікті асимптотасы ретінде жүйенің өзгерілмейтін бөлігінің жоғары жиілікті асимптотасын алайық. Онда қалаулы ЛАЖС орта жиілік асимптотасы жоғары жиілік асимптотасымен жиілік мәнінде түйіндестіріледі. Түйіндестіретін асимптотаны енқеюықлып өткіземіз. Осындай түйіндестіру қиыстыратын құрылғыныңжиілік кезінде ЛАЖС өзгертпейді.

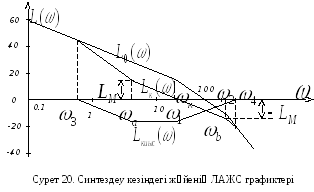
Ары қарай жәнебақылау жиіліктер кезіндегі фазаның артықтығын тексеру қажет. Артықтығы сәйкес болса, онда қалаулы ЛАЖС дұрыс таңдалды деп есептеуге болады.

Жүйенің қалаулы ЛАЖС,өзгерілмейтін бөлігінің ЛАЖС айырып,қисындыратын құрылғының ЛАЖС табамыз (сурет 20). ТабылғанЛАЖС бойынша қисындыратын құрылғының беріліс функциясыныңжәнеполиномдарын анықтауға болады. Олар тең

,

.

Өзгерілмейтін бөліктін кері байланыс енгілігенсон орнықтылығын бағалайық. Ол үшін MatLab ортасында келесі бұйырықтарын, программалау жолына енгізейік

>>w1=tf([200],[0.0005 0.06 1 200])

>>step(w1)

Нәтижесі сурет 21 қөрсетілген, расында зерттелетін жүйе орнықты емес, өтпелі процес амплитудасы өсетін тербелістер түрінде табылды.

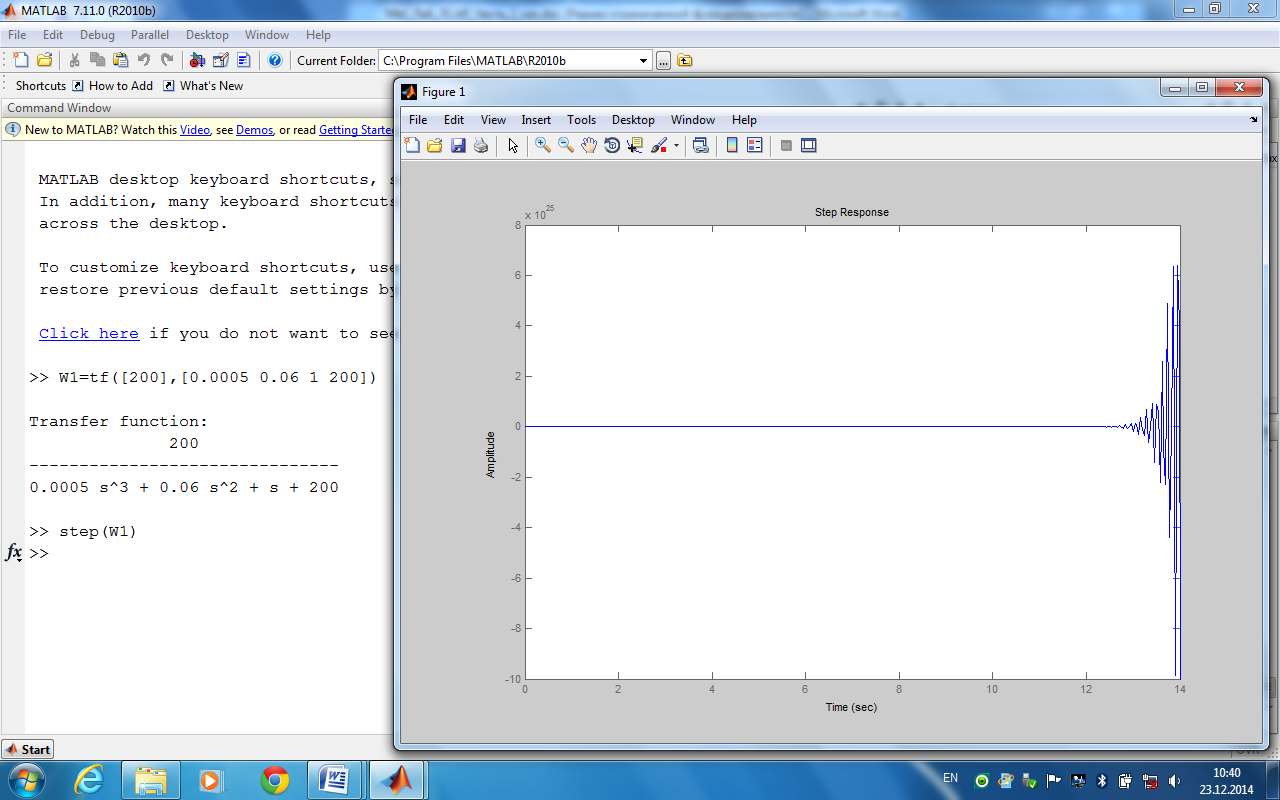
Сурет 21. Өзгерілмейтін бөлікті модельдеу нәтижелері

Қиыстыру құрылғыны тізбектеп қосқансон, түйықталмаған жүйенің беріліс функциясын былай , программалау жолына енгізіп амплитуда және фаза бойынша қорларын табайық

>>w1=tf([4 54 200],[0.00001 0.0022 0.1515 2.24 4 0])

>>margin(w1)

Сурет 22. Қиыстырылған жүйенің орнықтылық қорлары

Одан кейін, келесі бұйырықтарды енгізіп өтпелі процестің түрін табуға болады (сурет 23)

>>w1=tf([4 54 200],[0.00001 0.0022 0.1515 6.24 55 200])

>>step(w1)

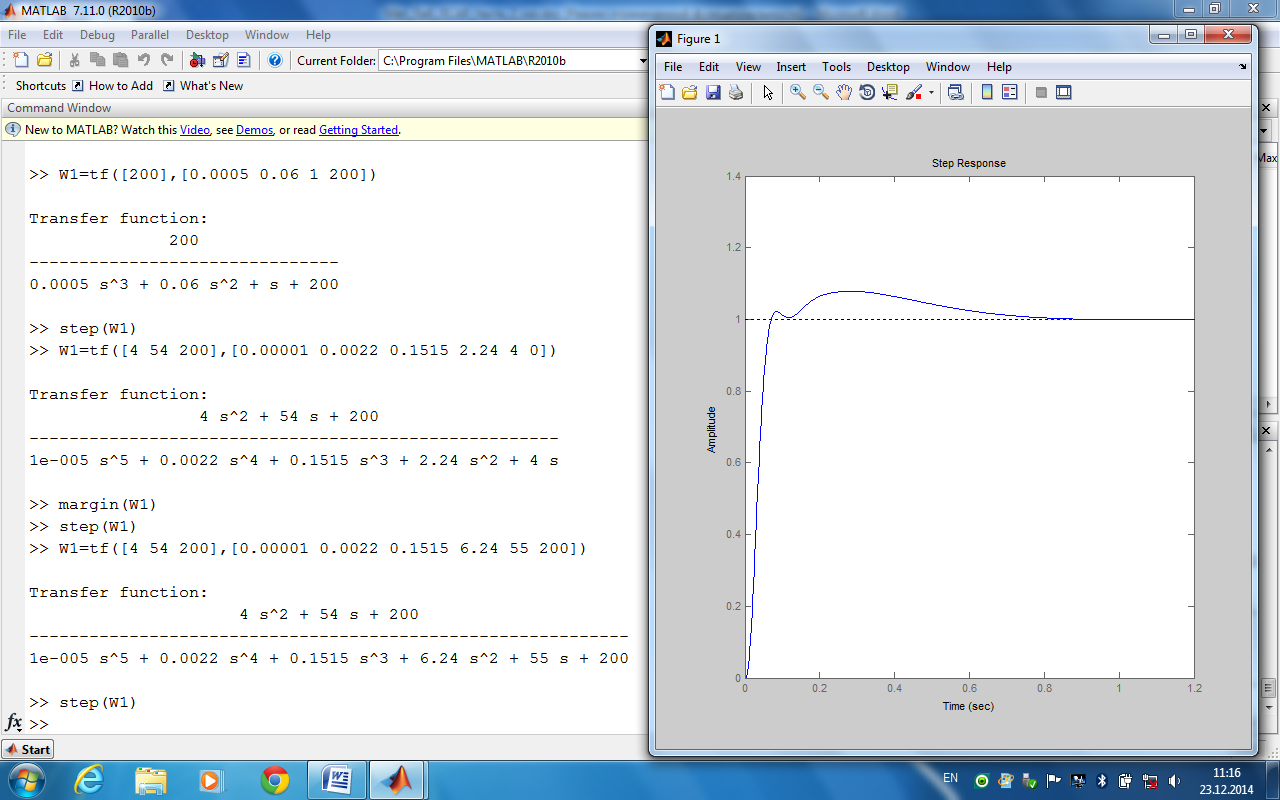
Сурет 23. Қиыстырылған жүйенің өтпелі процесі