
ТФКП
.docx
Задание №1.
Найти
все значения корня
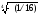 .
.
Решение:
Корень степени n комплексного числа z имеет n корней, который находятся по следующей формуле:
![]()
где φ=arg(z); k = 0, 1, …, n-1; z ≠ 0.
Т.о., подставляя различные значения k, мы найдем все значения данного корня:
1)
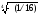 =
=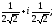 2)
2)
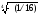 =
=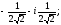
3)
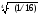 =
=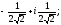 4)
4)
 =
=

Ответ:
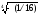 ={
={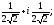
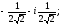
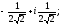
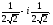 }.
}.
Задание №2.
Представить в алгебраической форме ch(1+πi/3).
Решение:
Перейдем к тригонометрическому косинусу:
ch(1+πi/3) = cos(1-π/3).
Разложив косинус по формуле косинуса разности получим:
cos(1-π/3) = cos(i)cos(π/3)+sin(i)sin(π/3);
Представим тригонометрическую функцию в виде показательных:
cos(i)cos(π/3)+sin(i)sin(π/3)
=
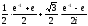 =
=
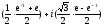 .
.
Ответ:
ch(1+πi/3)
=
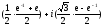 .
.
Задание №3.
Представить
в алгебраической форме Arctg( ).
).
Решение:
Т.к. функция arctg является многозначной и в общем виде определяется как
Arctg
z
=
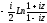 ,
,
То
при z
=
 получим:
получим:
Arctg( )
=
)
=
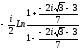 =
=
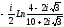 =
=
 .
.
Функция Ln(z), при z ≠ 0, определяется как функция , обратная показательной, при этом:
 =
=
 =
=
=
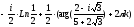 ≈
≈
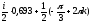 ,
где k=0,
±1, ±2,…
,
где k=0,
±1, ±2,…
Ответ:
Arctg(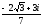 )
=
)
=
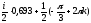 ,
k=0,
±1, ±2,…
,
k=0,
±1, ±2,…
Задание №4.

 Начертить
область, заданную неравенством |z|
≤ 1, arg(z+i)
>
Начертить
область, заданную неравенством |z|
≤ 1, arg(z+i)
>
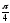 .
.

 Решение:
Решение:
0
1
Rez(z)
1
Im(z)
0


















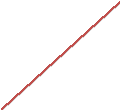

Задание №5.
Определить
вид кривой z
=
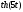 +
+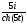 .
.
Решение:
Уравнение вида z = z(i) = x(t) + i*y(t) определяет на комплексной плоскости кривую, параметрические уравнения которой имеют вид x=x(t), y=y(t). Тогда:
x(t)
=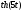 ,
y(t)
=
,
y(t)
=
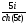 .
.
Выразим t:
x
=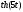 →
t
=
→
t
=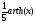 ;
;
y
=
 →
ch(5t)
=
→
ch(5t)
=
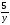 → t
=
→ t
=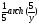 .
.
Получили уравнение кривой в виде F(x,y) = 0;
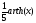 =
=
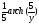 →
→
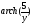 -
-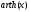 =
0.
=
0.
Ответ:
 -
-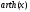 =
0.
=
0.
Задание №6.
Проверить, что v является мнимой частью аналитической функции. Восстановить аналитическую в окрестности точки z0 функцию f(z) по известной мнимой v(x, y) и значению f(z0).
v = 3x2y-y3; f(0)=1.
Решение:
Зная действительную часть аналитической функции узнаем её производную:
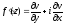
Найдем производную аналитической функции:
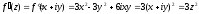 .
.
Т.к. производная существует, то v – мнимая часть данной функции. Теперь найдем саму функцию:
 .
.
Определим константу С:
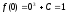 → С
= 1.
→ С
= 1.
Ответ: f(z) = z3 + 1.
Задание №7.
Вычислим интеграл от функции комплексной переменной по данной кривой:
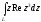 ;
L:
{|z|
= R,
Im
z
≥ 0}
;
L:
{|z|
= R,
Im
z
≥ 0}
Решение:
Изобразим кривую, по которой будет проходить интегрирование:
R
R
-R
-R
0






Перейдем к f(x, y) = u(x, y) + iv(x,y), где z = x + iy:
f(z) = (x+iy)Re(x2 +2ixy - y2) = x3 – xy2 + i(x2y - y3).
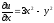 ,
,
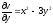 →
→
 ≠
≠ ;
;
Условие Коши-Римана не выполняются, значит, функция не является аналитической. Тогда представим кривую в параметрическом виде:
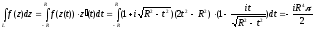
Ответ:
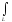
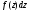
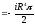 .
.
Задание №10.
Данную функцию разложить в ряд Лорена в окрестности z0:
f(z)
=
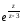 ,
z0
=3;
,
z0
=3;
Решение:
Перейдем
к новой переменной
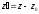 .
.
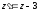 ;
;
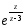 =
=
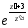 =
=
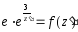 .
.
Теперь
остается найти разложение получившейся
функции от
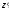 в
окрестности точки
в
окрестности точки
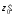 =
0. Для это используем разложение в ряд
Тейлора:
=
0. Для это используем разложение в ряд
Тейлора:
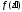 =
=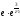 =
=
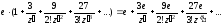
Возвратим переменные и получим разложение исходной функции в ряд Лорена:
f(z)
=
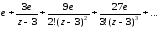
Ответ:
f(z)
=
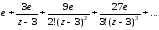
Задача №13.
Вычислить интеграл:
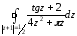 =
=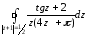 ;
;
Решение:
Найдем особые точки подынтегральной функции:
z = 0, z = -π/4;
Т.к. z = 0 не входит в ограниченную область контуром, то её можно не рассматривать.
Точка z = -π/4 является простым полюсом, поэтому найдем её вычет:
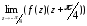 =
=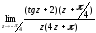 =
=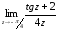 =
=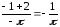 ;
;
Отсюда следует:
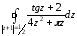 =
=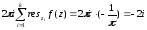 ;
;
Ответ:
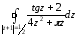 =
-2i.
=
-2i.
Задача №14.
Вычислить интеграл:
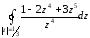 ;
;
Решение:
У данной функции существует только одна особая точка z = 0. Определим тип этой особой точки:
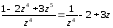
Считая данное выражение рядом Лорена по степени z, т.е. в окружности z= 0, мы приходим к тому, что точка z = 0 является полюсом 4-го порядка. В соответствие с этим, найдем вычет в данной точке:
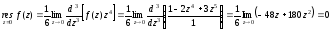 .
.
По основной теореме Коши о вычетах:
 ;
;
В данном случае:
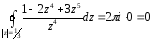 ;
;
Ответ:
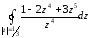 = 0.
= 0.
Задача №16.
Вычислить интеграл:
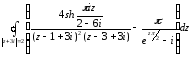 ;
;
Решение:
Разобьём данный интеграл на сумму двух интегралов:
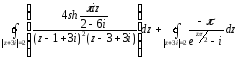
-
Для первого интеграла используем вычеты:
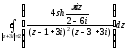
Подынтегральная функция имеет 2 особые точки: z1 = 1-3i и
z2 = 3(1-i). При этом точка z2 не охвачена контуром, по которому происходит интегрирование, поэтому не рассматривается.
Что качается z1, то она является полюсом второго порядка. Найдем вычет в ней:
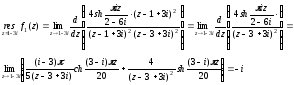 ;
;
Таким образом:
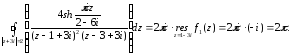
-
Рассмотрим второй интеграл:
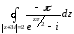 ;
;
Найдем особые точки подынтегральной функции, решив уравнение:
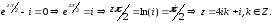
Из
всего полученного множества точек
только одна охвачена контуром
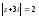 .
Точка z
= -3i
является простым полюсом. Найдем вычет
в этой точке (используем правило
Лопиталя):
.
Точка z
= -3i
является простым полюсом. Найдем вычет
в этой точке (используем правило
Лопиталя):
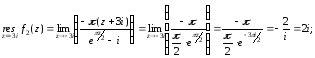
Таким образом:
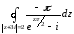 =
= 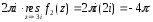 ;
;
-
Теперь найдем исходный интеграл как сумму составляющих его интегралов:
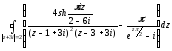 =
=
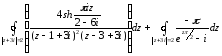 =
2π - 4π = 2π.
=
2π - 4π = 2π.
Ответ:
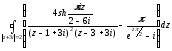 =
2π.
=
2π.
Задача №17.
Вычислить интеграл:
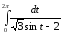
Решение:
Преобразуем данный интеграл в контурный, используя следующие выражения:
z = ek; cos t = (z+1/z)/2; sin t = (z - 1/z)/2i; dt = dz /iz;
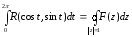 .
.
Перейдем к контурному интегралу:
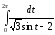

Подынтегральная
функция имеет 2 особые точки: z1
=
i/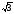 ,
z2
=
i
,
z2
=
i .
Точка z2
не попадает в область, ограниченную
контуром интегрирования. Точка z1
является простым полюсом, поэтому
следует вычислить в ней вычет:
.
Точка z2
не попадает в область, ограниченную
контуром интегрирования. Точка z1
является простым полюсом, поэтому
следует вычислить в ней вычет:
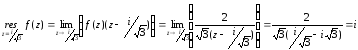 По
основной теореме Коши о вычетах:
По
основной теореме Коши о вычетах:
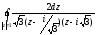 =
= ;
;
Ответ:
 =
=
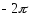 .
.
Задача №18.
Вычислить интеграл:
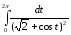
Решение:
Преобразуем данный интеграл в контурный, используя следующие замены:
z = ek; cos t = (z+1/z)/2; sin t = (z - 1/z)/2i; dt = dz /iz;
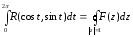
Теперь воспользуемся этими данными и перейдем к контурному интегралу:
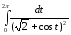 =
=
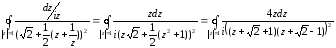 ;
;
Подынтегральная
функция имеет 2 особые точки: z1=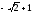 и z2
=
и z2
=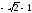 .
Точка
z2
не попадает в область ограниченную
контуром интегрирования. Точка z1
является
полюсом второго порядка. Вычислим вычет
в этой точке:
.
Точка
z2
не попадает в область ограниченную
контуром интегрирования. Точка z1
является
полюсом второго порядка. Вычислим вычет
в этой точке:
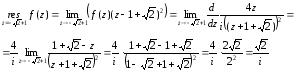
По основной теореме Коши о вычетах:
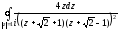 =
=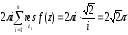
Ответ:
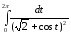
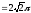 .
.
