Числовые характеристики непрерывных случайных величин

Определения числовых характеристик дискретных случай­ных величин распространяются и на непрерывные величины. Разница состоит в том, что вместо сумм в формулах (18.5) и (18.10) берутся их интегральные аналоги.

Определение 4. Математическим ожиданием непрерывной случайной величины X, возможные значения которой находят­ся на отрезке [а, b], называется определенный интеграл:

В том случае, когда возможные значения случайной вели­чины Х заполняют всю ось Ох, пределы интегрирования а и b бесконечны: а = -,b = . Возможны также случаи, ког­да один из пределов интегрирования бесконечен (возможные значенияХ лежат на полупрямой).

Определение 5. Дисперсией непрерывной случайной величины Х называется математическое ожидание квадрата ее отклонения:

Все сказанное выше о случаях бесконечных пределов интегрирования остается справедливым и для дисперсии.

Среднее квадратичекое отклоенние непрерывной случайной величины определяется, как и прежде, по формуле (18.15):

σ(Х) = .

Для вычисления дисперсии употребляется более удобная фор­мула, которая выводится из (18.37):

Пример 4. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X, заданной плотностью распределения на отрезке [0, 1]:

Решение. Согласно формулам (18.36), (18.38) и (18.15) по­следовательно вычисляем искомые величины:

Пример 5. Найти основные числовые характеристики непре­рывной случайной величины X, заданной функцией распреде­ления на положительной полуоси Ох:

Решение. Найдем сначала плотность распределения:

Затем, как и в предыдущем примере, вычисляем соответствуцющие интегралы; при их вычислении применяем правило интегрирования по частям для определенного интеграла. В итоге получаем искомые величины:

18.5. Основные распределения непрерывных случайных величин Равномерное распределение

Определение 1. Распределение вероятностей называется рав­номерным, если на интервале возможных значений случайной величины плотность распределения является постоянной.

Пусть на интервале (a, b) плотность распределения являет­ся постоянной величиной: f(x) = С. Определим значение С из условия (18.35):

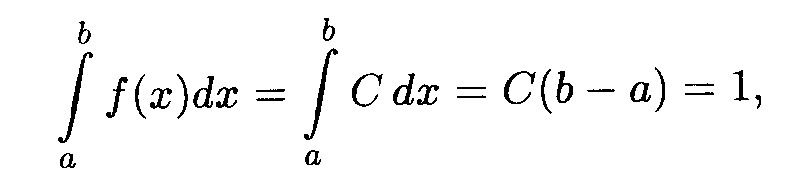
откуда получаем, что f(x) = С = 1/(b - а). Значит, искомая плотность равномерного распределения дается формулой

График плотности равномерного распределения указан на рис. 18.5.

Пример 1. Найти среднеквадратическое отклонение случай­ной величины X, распределенной равномерно на интерва­ле (1, 5).

Решение. Согласно формуле (18.39), плотность распреде­ления указанной случайной величины является ненулевой и равна 0,25 на интервале (1, 5). По формулам (18.36) и (18.38) последовательно вычисляем:

Пример 2. Радиус круга измерен приближенно на интервале (а, b). Полагая, что радиус является случайной величиной X, распределенной равномерно в этом интервале, найти матема­тическое ожидание и дисперсию площади круга.

Решение. Площадь круга также является случайной ве­личиной, вычисляемой по формуле Y = πX²; она имеет то же равномерное распределение, что и случайная величина X. По формулам (18.36) и (18.38) получаем