Среднее квадратическое отклонение

Одной из основных оценок рассеяния возможных значе­ний случайной величины служит среднее квадратическое от­клонение.

Определение 4. Средним квадратическим отклонением слу­чайной величины Х (стандартом) называется квадратный ко­рень из ее дисперсии:

Согласно этому определению, из свойства 3 и формулы (18.13) следует, что в случае суммы взаимно независимых слу­чайных величин справедлива формула

Пример 9. Найти дисперсию и среднее квадратическое отклонение случайной величины X, заданной следующим распределением:

Решение. Имеем М(Х) = 2,6. Составим таблицу распре­деления случайной величины X²:

Отсюда получаем, что М(Х²) = 14,4. По формулам (18.11) и (18.15) окончательно получаем искомые значения D(X) и. σ(Х):

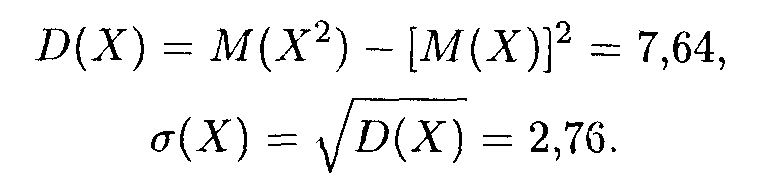
Пример 10. Законы распределения независимых случайных величин Х и Y приведены соответственно в таблицах:

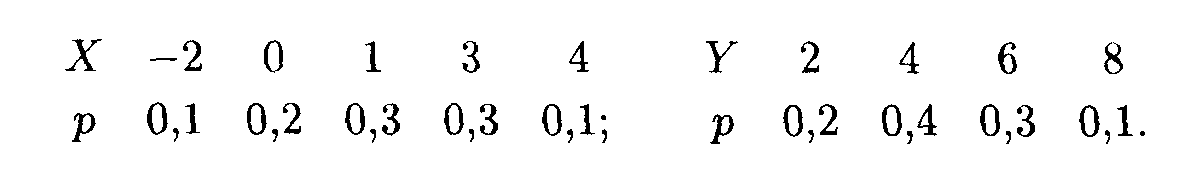
Найти дисперсию и среднее квадратическое отклонение слу­чайной величины Z = 2Х + 3Y.

Решение. Согласно свойствам 2 и 3 дисперсии (формулы (18.12) и (18.13)), имеем

Для вычисления дисперсий D(X) и D(Y) составляем соответ­ствующие таблицы — законы распределения случайных вели­чин Х² и Y²:

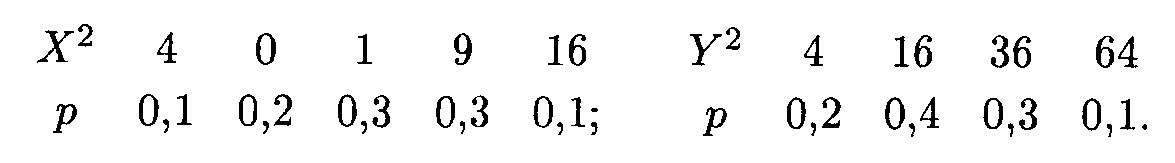
Отсюда получаем

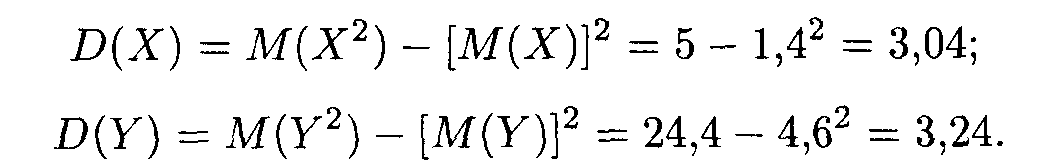
Искомые дисперсия и среднее квадратичное отклонение слу­чайной величины Z равны:

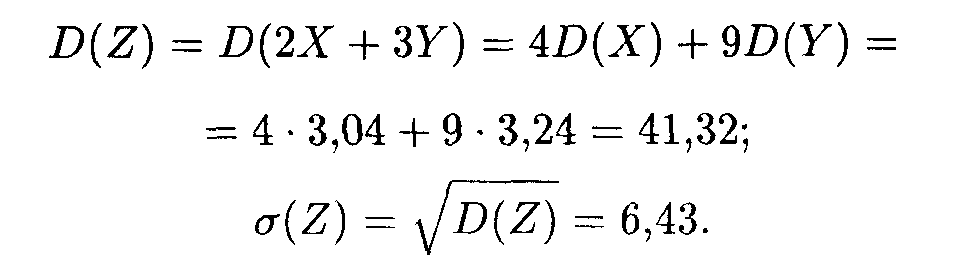
Пример 11. В условиях примера 8 найти математическое ожи­дание и среднее квадратическое отклонение прибыли при п = 1000, р = 0,8, S = 100 тыс. р. и r = 30%.

Решение. Ставка ссудного процента удовлетворяет усло­вию, чтобы математическое ожидание прибыли было положи­тельным: 30 > 100 (1 - 0,8) / 0,8. Математическое ожидание при­были:

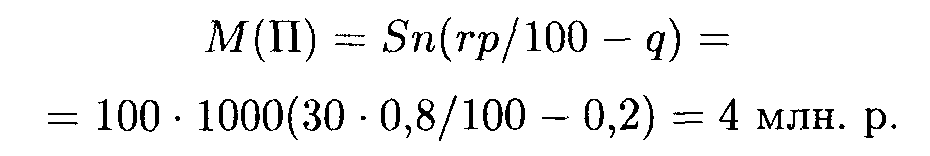
Среднее квадратическое отклонение прибыли:

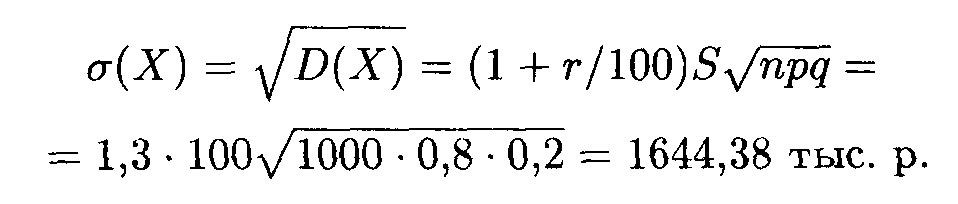
Начальные и центральные моменты

Определение 5. Начальным моментом порядка k случай­ной величины Х называется математическое ожидание вели­чины Х^k:

В частности,

и тогда формула (18.11) для вычисления дисперсии принимает вид

Определение 6. Центральным моментом порядка k случай­ной величины Х называется математическое ожидание k-й сте­пени отклонения:

В частности, согласно формуле (18.9), μ₁ = 0, а дисперсия слу­чайной величины Х является центральным моментом второго порядка:

Соотношения, связывающие начальные и центральные мо­менты, также могут быть легко получены. Приведем их здесь для моментов третьего и четвертого порядков (они наряду с моментами первого и второго порядков широко применяются в статистике):

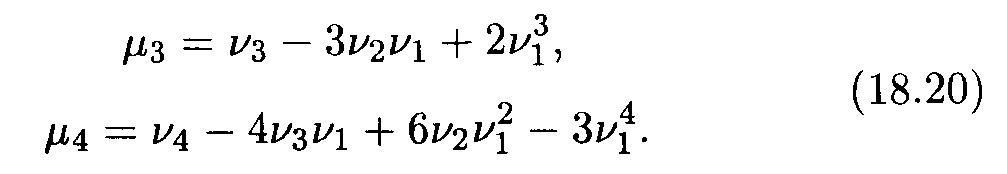
Моменты более высоких порядков применяются крайне редко.

Моменты, рассмотренные в этом разделе, называют те­оретическими. В отличие от них моменты, вычисляемые по данным наблюдений в математической статистике, называют эмпирическими.

18.3. Система двух случайных величин Двумерная случайная величина

До сих пор мы рассматривали дискретные случайные ве­личины, которые называют одномерными: их возможные зна­чения определялись одним числом. Кроме одномерных вели­чин рассматривают также величины, возможные значения ко­торых определяются несколькими числами. Двумерную слу­чайную величину обозначают через (X, Y); каждая из величин X и Y называется компонентой (составляющей). Обе величи­ны Х и Y, рассматриваемые одновременно, образуют систему двух случайных величин. Например, при штамповке стальных пластинок их длина и ширина представляют собой двумерную случайную величину.

Определение 1. Законом распределения двумерной случай­ной величины (X, Y) называют множество возможных пар чи­сел (x_i, y_j) и их вероятностей p(x_i, y_j). Двумерную случайную величину можно трактовать как случайную точку А(Х, Y) на координатной плоскости.

Закон распределения двумерной случайной величины обыч­но задается в виде таблицы, в строках которой указаны воз­можные значения x_i случайной величины X, а в столбцах — возможные значения y_j случайной величины Y, на пересече­ниях строк и столбцов указаны соответствующие вероятности p_ij. Пусть случайная величина Х может принимать п значе­ний, а случайная величина Y - т значений. Тогда закон рас­пределения двумерной случайной величины (X, Y) имеет вид

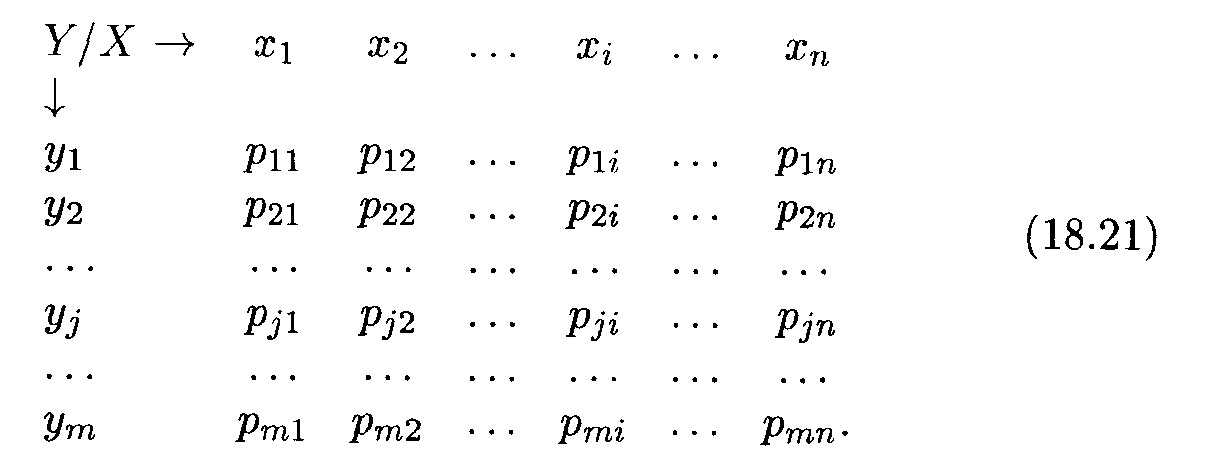
Из этой таблицы можно найти законы распределения каждой из случайных компонент. Например, вероятность того, что слу­чайная величина Х примет значение х_k, равна, согласно тео­реме сложения вероятностей независимых событий,

Иными словами, для нахождения вероятности Р(х_k) нужно просуммировать все т вероятностей по k-му столб­цу таблицы (18.21). Аналогично получается вероятность то­го, что случайная величина Y примет возможное значение у_r: Р(у_r) получается суммированием всех n вероятностей r-й стро­ки таблицы (18.21) (r = 1, 2, ... ,m). Отсюда следует, что сумма всех вероятностей в законе распределения (18.21) равна единице:

Пример 1. Задано распределение двумерной случайной вели­чины:

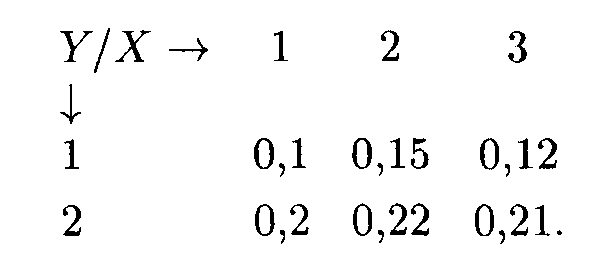
Найти распределения Х, Y и Х + Y.

Решение. В нашем случае возможные значения случайной величины X: х₁ = 1, х₂ = 2, x₃ = 3. Тогда, согласно формуле (18.22), имеем P(x₁) = 0,1 + 0,2 = 0,3, P(x₂) = 0,15 + 0,22 = 0,37, Р(x₃) = 0,12 + 0,21 = 0,33. Отсюда получаем закон распреде­ления X:

Аналогично получаем и для распределения Y: у₁ = 1, y₂ = 2; P(y₁) = 0,1 + 0,15 + 0,12 = 0,37, P(y₂) = 0,2 + 0,22 + 0,21 = 0,63;

Теперь найдем распределение X+Y. Возможные значения этой случайной величины: 2, 3, 4 и 5. Соответствующие вероятнос­ти Р(2) = 0,1, Р(3) = 0,15 + 0,2 = 0,35, Р(4) = 0,12 + 0,22 = 0,34, Р(5) = 0,21. Отсюда находим искомое распределение:

В случае системы двух случайных величин используются кроме математических ожиданий и дисперсий еще и другие числовые характеристики, описывающие их взаимосвязь.