
metod1_KI_dlya_studentov
.pdf
Построенный тетраэдр проецируется в правильную область D , расположенную
вплоскости XOY , и любая прямая, проходящая через внутреннюю точку D перпендикулярно этой области, пересекает граничные поверхности тетраэдра в двух точках, в одной нижней и одной верхней. Т.е. тетраэдр занимает
впространстве правильную область V .
V x, y, z x, y Dxy , 0 z 1 x y
Рисунок 5. 7
При этом |
|
|
|
|
|
|
|
1 x y |
|
|
. |
|
|
dxdydz |
|
|
|
||||||
|
f |
|
x, y, z |
|
|
dxdy |
|
f |
|
x, y, z dz |
|
V |
|
|
|
|
|
D |
|
0 |
|
|
|
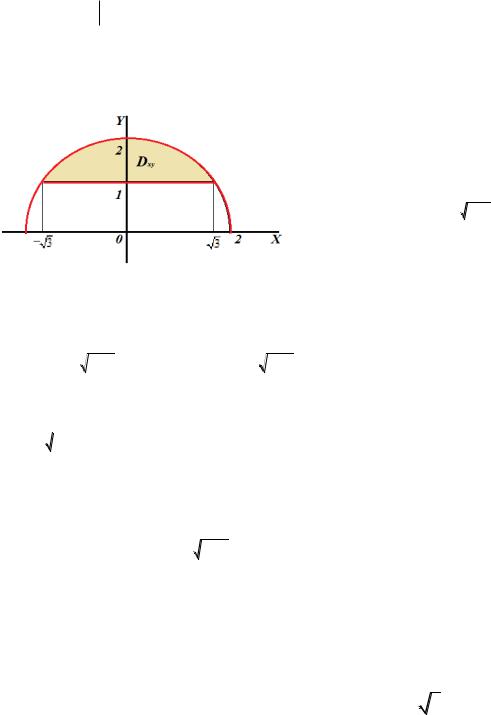
Область D является y -правильной. Для всех её точек 0 x 1,0 y 1 x . Переходя к повторному интегралу, расставляем пределы интегрирования.
|
1 |
1 x |
1 x y |
|
|
f x, y, z dxdydz dx |
dy |
|
f x, y, z dz . |
||
V |
0 |
0 |
|
0 |
|
Самостоятельно измените порядок интегрирования, спроецировав тетраэдр в другую координатную плоскость.
Пример 5.2 Вычислим объём тела, ограниченного поверхностями:
z x2 y2 , z 4, y 1, |
y 1 . |
||||
Решение. |
Построим заданные |
||||
поверхности и выделим тело, объём |
|||||
которого требуется вычислить. (См. |
|||||
рис.5.3) |
|
|
Полученное |
||
тело проецируем в плоскость XOY и |
|||||
получаем область Dxy - сегмент круга. |
|||||
Определим границы сектора. Плоскость |
|||||
z 4 пересекает параболоид по |
|||||
окружности, которая проецируется в |
|||||
часть границы |
области D : |
||||
|
|
y |
x2 |
y2 4 . |
|
z x |
2 |
|
|||
|
|
2 |
|
|
|
Рисунок 5. 3 |
z 4 |
|
|
|
31 |
Область V , занимаемая в пространстве телом T , является правильной и
V x, y, z x, y Dxy , x2 y2 z 4
Для удобства дальнейших рассуждений построим область Dxy на отдельном
рисунке 5.4. Заметим, что область и само тело являются симметричными относительно плоскости YOZ .
Рассматривая область Dxy как x- правильную, с учётом симметрии,
расставим пределы |
в |
повторном |
|
|
|
|
|
2 |
4 y2 |
|
4 |
интеграле: V 2 dy |
|
dx |
dz . |
1 |
0 |
|
x2 y2 |
Рисунок 5.4
Ниже приведено подробное вычисление данного интеграла.
|
|
|
2 |
|
4 y2 |
|
|
4 |
|
|
|
|
2 |
4 y2 |
z |
|
4x2 y2 dx |
|
|
|
|
|
|
|
|
|
|||||||||||||||
V 2 dy |
|
dx |
dz 2 dy |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
1 |
0 |
|
x2 y2 |
|
|
|
1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
4 y2 |
4 y2 x2 dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
2 dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
|
|
|
|
|
|
|
x3 |
|
4 y2 |
|
4 |
|
2 |
|
|
|
|
3 |
|
|
y 2sin t |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
2 |
4 y2 x |
|
|
|
|
|
|
|
|
|
|
dy |
|
|
|
4 y2 |
|
|
dy dy 2costdt |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||||||||||||||||||||||||||
3 |
|
3 |
|
||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
; |
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|||
|
64 2 |
cos4 tdt |
16 3t |
|
sin 2t |
|
sin 4t |
2 |
|
3 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
3 . |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
3 |
2 |
|
|
|
|
|
|
|
8 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32
Занятие 6.
Замена переменных в тройном интеграле. Цилиндрические, сферические координаты. Якобиан для цилиндрических и сферических координат. Вычисление тройного интеграла в цилиндрических и сферических координатах. Вычисление объемов тел с помощью тройного интеграла. 1. Замена переменных в тройном интеграле.
Пусть в пространстве OUVW задана область V . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Теорема. Если непрерывно дифференцируемые функции |
|
|
|
|
|
||||||||||||||||||
x x u,v, w , y y u,v, w , z z u,v, w взаимно однозначно отображают |
|||||||||||||||||||||||
область V |
пространства OUVW на область V в пространстве OXYZ и |
||||||||||||||||||||||
|
|
|
|
|
|
x |
y |
|
z |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x, y, z |
|
|
u |
u |
|
u |
|
|
|
|
|
|
|
|||||||
якобиан отображения V ' V |
J |
|
|
x |
y |
z |
|
|
отличен от нуля, |
||||||||||||||
|
v |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
u,v, w |
v |
v |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
x |
|
y |
|
|
z |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
w |
|
w |
|
|
w |
|
|
|
|
|
|
|
|||||
то справедлива формула |
x u,v, w , y u,v, w , z u,v, w |
|
|
|
|
||||||||||||||||||
f x, y, z dxdydz f |
|
J |
|
dudvdw (6.1) |
|||||||||||||||||||
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
V |
V ' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.Цилиндрическая система координат.
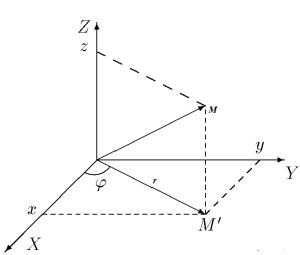
В цилиндрической системе координат положение точки M в пространстве
|
|
|
|
|
характеризуется тремя координатами: |
||
|
|
|
|
|
r -расстояние от начала координат до |
||
|
|
|
|
|
проекции точки M на плоскость XOY , |
||
|
|
|
|
|
-угол поворота радиус-вектора |
||
|
|
|
|
|
проекции точки на эту же плоскость |
||
|
|
|
|
|
относительно оси OX , z -аппликата |
||
|
|
|
|
|
точки. (Первые две координаты точки |
||
|
|
|
|
|
совпадают с полярными координатами |
||
|
|
|
|
|
её проекции на плоскость XOY - см. |
||
|
|
|
|
|
рис 6.1). |
Связь между |
|
|
|
|
|
|
цилиндрическими и декартовыми |
||
|
Рисунок 6.9 |
|
|
координатами выглядит следующим |
|||
|
|
|
|
|
образом: |
|
|
x r cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y r sin |
|
0 |
2 , |
0 r , |
z . (6.2) |
||
|
, где |
||||||
|
|
|
|
|
|
||
z z |
|
|
|
|
|
|
|
33
|
|
|
r . |
|
|||||||||
Самостоятельно вычислите Якобиан и убедитесь в том, что |
J |
|
|||||||||||
Следовательно, переходя к цилиндрическим координатам, имеем |
|
||||||||||||
f x, y, z dxdydz f r cos ,r sin , z rd drdz |
(6.3) |
||||||||||||
V |
|
|
|
|
V |
|
|
|
|
|
|
|
|
Замечание 1. Целесообразно переходить к цилиндрической системе |
|
||||||||||||
координат, если уравнения поверхностей, ограничивающих тело, или |
|
||||||||||||
подынтегральная функция зависят от |
x2 |
y2 |
, т.к. при этом переходе |
||||||||||
x2 y2 r2 . |
Если область V правильная и |
|
|
||||||||||
V x, y, z |
|
|
x, y D , |
z x, y |
z z |
2 |
x, y |
|
|
||||
|
|
|
|||||||||||
|
|
|
|
|
xy |
1 |
|
|
, то |
|
|
||
|
|
|
|
|
|
2 |
r , |
|
|
|
|
|
|
f x, y, z dxdydz rd dr |
|
f r cos ,r sin , z dz , |
(6.3а) |
||||||||||
V |
|
|
|
|
Dxy |
1 r , |
|
|
|
|
|
|
|
где z1 x, y 1 r, , z2 x, y 2 x, y . |
|
|
|
|
|
|
|||||||
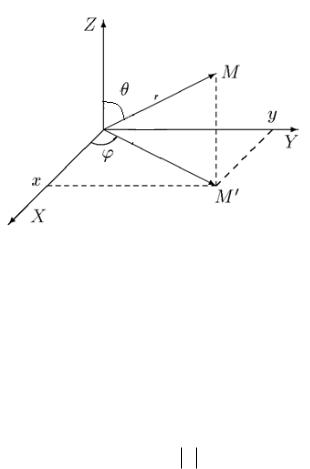
3.Сферическая система координат. |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
В сферической системе координат положение |
|||||||
|
|
|
|
|
|
|
точки в пространстве характеризуется |
||||||
|
|
|
|
|
|
|
тоже тремя координатами: r - |
|
|||||
|
|
|
|
|
|
|
расстояние от начала координат до |
||||||
|
|
|
|
|
|
|
самой точки M , -угол поворота |
||||||
|
|
|
|
|
|
|
радиус-вектора проекции M точки |
||||||
|
|
|
|
|
|
|
M на плоскость XOY относительно |
||||||
|
|
|
|
|
|
|
оси OX , -угол между радиус- |
||||||
|
|
|
|
|
|
|
вектором точки M и осью OZ |
( см. |
|||||
|
|
|
|
|
|
|
рис. 6.2). Связь между сферическими |
||||||
|
|
|
|
|
|
|
и декартовыми координатами |
|
|||||
|
|
|
|
|
|
|
выглядит следующим образом: |
||||||
Рисунок 6.10 |
|
|
|
|
|
|
|
|
|
||||
x r sin cos |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y r sin sin |
, |
|
|
(6.4) |
|
где |
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z rco s |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 2 , |
0 , |
0 r . При этом |
x2 y2 z2 r2 . |
|
|
||||||||
Самостоятельно вычислите Якобиан и убедитесь в том, что при переходе к сферической системе J r2 sin . Следовательно, переходя к сферическим
координатам, имеем:
34
f x, y, z dxdydz f r sin cos ,r sin sin ,rcos r2 sin d d dr (6.5)
V V
Замечание 2. В сферических координатах уравнение сферы x2 y2 z2 R2 принимает вид r R , уравнение кругового конуса k 2 x2 y2 z2
принимает вид arctgk . Поэтому целесообразно переходить к этим координатам, если в условии задачи присутствуют конусы и сферы. Замечание 3. Чтобы преобразовать тройной интеграл в сферической системе координат в повторный, можно поступить следующим образом. Пересечём тело, занимающее область V , полуплоскостью, проходящей через ось OZ , и выделим площадку D , которая при этом получится. Через ось OZ построим две полуплоскости, которые образуют двухгранный угол , внутри которого заключено тело. Для этого двухгранного угла, а значит, и для области V
1 2 . |
И тогда |
|
|
2 |
|
f x, y, z dxdydz d f r sin cos ,r sin sin ,r cos r2sin d dr |
||
V |
1 |
D |
|
|
(6.5а) |
В двойном интеграле по области D пределы расставим как в полярной системе координат с той разницей, что переменная меняется от вертикальной оси, где она равна нулю, возрастая против часовой стрелки.
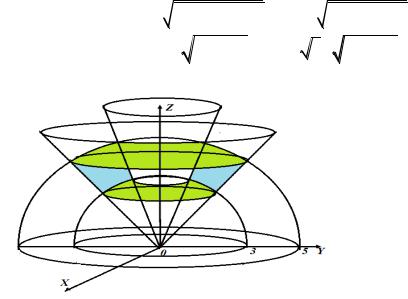
Пример 6.1. Вычислим объём тела, заключённого между двумя
полусферами z 
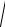 25 x2 y2 и z
25 x2 y2 и z 
 9 x2 y2 и двумя коническими
9 x2 y2 и двумя коническими
|
|
|
|
|
|
|
|
поверхностями z |
x2 y2 |
и z |
3 |
x2 y2 . |
|
||
|
|
|
|
|
Решение. Согласно |
||
|
|
|
|
|
вышесказанному, уравнения сфер |
||
|
|
|
|
|
в сферических координатах |
||
|
|
|
|
|
примут вид r 5 и r 3 . |
||
|
|
|
|
|
Уравнения конусов, являющихся |
||
|
|
|
|
|
телесными углами, примут вид |
||
|
|
|
|
|
|
и соответственно, в |
|
|
|
|
|
|
4 |
6 |
|
чём легко убедиться,заменив в уравнениях поверхностей
Рис.6.3 |
декартовы переменные |
|
сферическими (см. (6.4)). |
||
|
||
|
Тогда по формуле (6.5) можно |
|
|
составить тройной интеграл для |
|
|
вычисления объёма в сферической |
|
|
системе координат, считая |
35
подынтегральную функцию равной единице.
V 1 r2 sin d d dr
V
Чтобы преобразовать тройной интеграл в сферической системе координат в повторный (см. замечание 3), пересечём тело, занимающее область V , полуплоскостью, проходящей через ось OZ , и выделим площадку D , которая при этом получится (на рис. 6.3 эта площадка справа выделена синим). Для того, чтобы получить всё тело, площадку D надо провращать вокруг оси OZ на угол 2 . Тогда
2
V d r2sin d dr
0D
Вдвойном интеграле по области D пределы расставим как в полярной системе координат с той разницей, что переменная меняется от вертикальной оси, где она равна нулю, возрастая против часовой стрелки.
Т.е. D |
|
|
|
|
,3 |
r |
5 |
|
. |
И окончательно, получаем |
|||
, r | |
|
|
|
||||||||||
|
|
6 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
4 |
|
5 |
|
|
|
|
|
|
|
|
|
|
V d sin d r2dr 39 |
|
|
|
|
|
. |
|||||||
3 |
2 |
||||||||||||
0 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
Пример 6.2. Найдём объём тела, заданного системой неравенств
x |
|
y |
|
z |
|
2z |
|
2 |
|
2 |
|
2 |
|
|
|
y2 |
z |
, с помощью тройного интеграла. |
||
x2 |
|
|||||
|
|
|
|
|
|
|
Решение. Построим сферу и параболоид, заданные в условии, и выделим тело, ограниченное ими.
|
Замечание. Уравнения обеих |
|
|
поверхностей имеют вид f x2 y2 , z 0 , |
|
|
что говорит о том, что это поверхности |
|
|
вращения вокруг оси OZ . Поэтому тело |
|
|
вращения, ограниченное ими, можно |
|
|
построить следующим образом. Строим |
|
|
линии пересечения поверхностей с |
|
|
полуплоскостью x 0, y 0 , выделяем |
|
|
область D , ограниченную этими линиями |
|
|
(на рис. 6.4 эта область справа выделена |
|
|
жёлтым цветом), и вращаем D вокруг оси |
|
|
OZ . Получаем заданное в условии задачи |
|
Рисунок 6.4 |
||
|
||
|
36 |
|
|

тело, которое в пространстве занимает область V (см. рис. 6.4).
1 способ. Рассмотрим решение задачи в цилиндрической системе координат. Заданное тело заключено внутри цилиндра с образующей, параллельной оси OZ , проходящей через линию пересечения сферы и параболоида. Чтобы составить его уравнение, которое совпадёт с уравнением границы области Dxy (см. рис. 6.4), необходимо из системы уравнений этих поверхностей
исключить переменную z .
x |
|
y |
|
z |
|
2z |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
2 |
|
|
|
2 |
|
|
2 |
|
|
x2 |
y2 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 z |
|
|
|
|
|
|
|
|
|
|
||||||
x2 y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Область Dxy , на которую проектируется тело, представляет собой круг |
|
|||||||||||||||||||||
x |
2 |
|
y |
2 |
|
1. |
|
Область |
V |
x, y, z |
|
|
x, y D , |
z x, y z z |
2 |
x, y |
||||||
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
xy |
1 |
|
|
|||||||
является правильной. Перейдём к цилиндрической системе координат. |
|
|||||||||||||||||||||
После замены переменных (см. (6.2)) получим: |
|
|
|
|
||||||||||||||||||
уравнение границы области Dxy - |
r 1, |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
уравнение нижней части сферы- z 1 1 r2 , |
|
|
|
|
||||||||||||||||||
уравнение параболоида- |
z=r2. |
|
|
|
|
|
|
|
|
|
||||||||||||
Обратите внимание на прямую линию в левой части рисунка 6.4. Мы видим, что при возрастании переменной z сферическая поверхность ограничивает тело снизу, а параболическая – сверху.
Объём тела вычислим как тройной интеграл, где f x, y, z 1 (см. свойства).
|
|
2 |
r , |
|
V dxdydz rd dr |
|
dz |
(см. (6.3а)). |
|
V |
D |
1 r , |
|
|
Область D ,r | 0 2 ,0 r 1 является радиально правильной.
Расставим пределы в повторном интеграле и вычислим его.
|
|
|
|
|
2 |
1 |
|
|
|
r2 |
1 |
|
|
|
||||||
V rd drdz d rdr |
|
|
dz 2 (r2 |
1 r 2 1)rdr |
||||||||||||||||
V |
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
||
|
|
|
|
|
|
|
|
1 |
1 r2 |
|
|
|
||||||||
|
|
4 |
|
|
|
3 |
|
|
2 |
|
|
1 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
r |
|
|
1 |
1 r2 2 |
|
r |
|
|
|
|
|
|
|
|||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
4 |
|
3 |
|
|
2 |
|
|
0 |
|
6 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 способ. Рассмотрим решение этой же задачи в сферической системе координат.
V dxdydz r2 sin d d dr .
V V
Преобразуем уравнения поверхностей. Уравнение сферы примет вид: r 2cos .
37
Уравнение параболоида: r |
|
cos |
. |
|
|
|
|
|
|
|
|||
|
|
sin2 |
|
|
||
Чтобы расставить пределы интегрирования в повторном интеграле, |
|
|||||
пересечём область V полуплоскостью, проходящей через ось OZ . Получим |
||||||
плоскую область D (на рис. 6.3 она справа закрашена жёлтым цветом). Так |
||||||
как область V была получена при вращении этой площадки D вокруг оси |
||||||
OZ , для всех точек V переменная 0,2 . |
|
|
||||
2 |
|
|
|
|
||
И тогда V dxdydz |
d r2sin d dr . |
(см. (6.5а)) |
|
|||
V |
0 |
D |
|
|
||
Область D является радиально правильной и для всех её точек |
, а |
|||||
|
|
|
|
|
4 |
2 |
переменная r меняется от r параболоида до r |
сферы. (Обратите внимание на |
||||||||||||||||||||
прямую линию в правой части рисунка 6.3) |
|
|
|
|
|
|
|
||||||||||||||
В соответствии с данными рассуждениями составим повторный тройной |
|||||||||||||||||||||
интеграл в сферической системе координат и вычислим его: |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
2cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
V d sin d r2dr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
0 |
|
|
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
sin2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
2 |
|
|
|
2 |
2 |
|
cos3 |
|
d |
|
|
|
|
|
|
|
|||
|
|
cos3 sin d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3 |
3 |
|
sin |
3 |
|
|
sin |
2 |
|
3 |
6 |
6 . |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
4 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
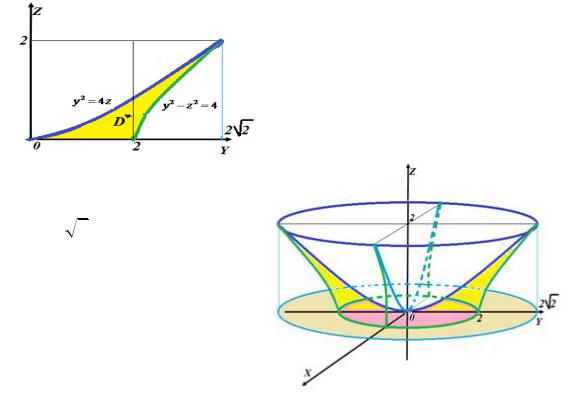
Пример 6.3. Найдём объёма тела, ограниченного поверхностями |
|||||||||||||||||||||
x2 y2 z2 4, |
x2 y2 4z, |
|
z 0. |
|
|
|
|
|
|
|
|
|
|
||||||||
Решение. Построим тело, ограниченное данными поверхностями, учитывая то, что оно является телом вращения, поскольку уравнения всех
поверхностей зависят от x2 y2 . Для этого
пересечём поверхности полуплоскостью x 0, y 0 и выделим
область D , ограниченную полученными линиями, а менно, гиперболой y2 z2 4 и параболой y2 4z . (см. рис. 6.5) Найдём
точку
пересечения этих кривых. Она имеет координаты
y 2
 2, z 2.
2, z 2.
При вращении этой области вокруг оси OZ получим (рис. 6.6)
38

Р
и
с
у
н
о
к
6
.
6
пространственную область V , которую занимает заданное тело. Эта область не является правильной, так как снизу ограничена двумя поверхностями, параболоидом и плоскостью z 0 . Поэтому для вычисления требуемого объёма придётся разбить область на две правильные и тогда V V1 V2 ( см.
рис. 6.6). В этом случае
|
|
|
|
|
|
|
1 |
x |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
V |
x, y, z |
|
x, y D , 0 |
z |
|
|
|
y |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Область D1 на рис. 6.6 выделена тёмным сиреневым цветом. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
x |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
2 |
|
2 |
|
|||||
V |
x, y, z |
|
x, y D , |
x |
|
y |
|
4 |
z |
|
|
y |
|
|
. |
||||||
|
|
|
|
|
|||||||||||||||||
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
Область D2 выделена светлым сиреневым цветом. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Перейдём в цилиндрическую систему координат (см. (6.2)) |
|
|
и составим оба |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 r , |
|
|
|
|||||
интеграла. |
Из формулы |
V dxdydz rd dr |
|
|
dz следует: |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
1 r , |
|
|
|
||||||||
|
|
1 |
r |
2 |
|
|
|
|
|
|
|
|
1 |
|
r |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V d |
rdr |
|
|
d rdr |
|
|
|
dz 8 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
dz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
2 |
2 |
4 |
|
|
2 |
8 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
0 |
|
0 |
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
r2 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
2-ой способ.Искомый объём можно найти иначе, а именно как V V3 V4 . |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
x |
2 |
|
|
2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
(См. рис. (6.6)) |
Здесь V |
x, y, z |
|
x, y D, 0 z |
|
|
|
|
y |
|
|
, причём |
|||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
область D - круг x2 y2 |
8 , а V4 x, y, z |
|
x, y D2 , 0 z |
|
|
|
|
. |
|||||||||||||||||||||||||||||
|
|
x2 y2 |
4 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
r |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
r2 4 |
|
|
8 |
|
||||||||
|
|
|
|
|
8 |
|
|
|
4 |
|
|
|
|
8 |
|
|
|
|
|
|
|||||||||||||||||
И в этом случае |
|
|
V d rdr |
dz d |
rdr |
|
|
|
|
|
dz |
. |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
0 |
0 |
|
|
|
|
0 |
0 |
|
2 |
|
|
|
|
0 |
|
|
|
|
|
3 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
3-ий способ.Наконец, можно изменить порядок интегрирования и составить повторный интеграл следующим образом:
2 |
2 |
2 |
|
4 z2 |
|
8 |
|
|
|
||
V d rdrdz d dz |
|
|
|
|
rdr |
. (В этом случае вращаем область |
D |
||||
|
3 |
||||||||||
0 D |
0 |
0 |
2 z |
|
|
|
|
||||
вокруг оси OZ так, что 0 2 , а интеграл |
rdrdz представляем как |
|
|||||||||
D
повторный по r -правильной области D r, z | 0 z 2, 2
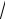 z r
z r 
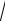 4 z2
4 z2
(см. рис.6.6, жёлтая область справа).
39
Занятие 7.
Приложение тройных интегралов (вычисление массы тела переменной плотности; статических моментов тел относительно координатных плоскостей; координат центра масс тел и их моментов инерции относительно осей координат. Несобственный двойной интеграл 1-го рода. Вычисление интеграла Пуассона
1.Механические приложения тройного интеграла. Следующие формулы аналогичны соответствующим формулам для двумерного случая.
Масса тела объёма V с переменной плотностью x, y, z .
M x, y, z dxdydz |
(7.1) |
V |
|
Статические моменты тела относительно координатных плоскостей.
K yz |
x x, y, z dxdydz |
|
|||||||||
|
|
|
|
|
|
V |
|
|
|
||
Kxz |
y x, y, z dxdydz |
(7.2) |
|||||||||
|
|
|
|
|
|
V |
|
|
|||
|
|
|
|
|
|
|
|
|
|||
Kxy |
z x, y, z dxdydz |
|
|||||||||
|
|
|
|
|
|
V |
|
|
|
||
|
|
Координаты центра масс тела. |
|||||||||
|
|
|
|
|
|
M |
|
|
|
||
x |
|
|
1 |
|
|
|
x x, y, z dxdydz |
|
|||
|
|
|
|
|
|
||||||
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
y |
|
|
1 |
|
|
y x, y, z dxdydz |
|
||||
|
M |
(7.3) |
|||||||||
|
c |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
M |
|
|
|
|||
z |
|
|
1 |
|
|
z x, y, z dxdydz |
|
||||
c |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
Моменты инерции тела относительно осей координат. |
|||
Ix |
y2 |
z2 |
x, y, z dxdydz |
|
V |
|
|
I y |
x2 |
z2 x, y, z dxdydz |
|
|
V |
|
(7.4) |
Iz |
x2 |
y2 |
x, y, z dxdydz |
V
Момент инерции тела относительно начала координат.
I0 x2 y2 z2 x, y, z dxdydz |
Ix I y Iz |
. |
|
||
|
(7.5) |
||||
V |
|
2 |
|
|
|
|
|
|
|
|
|
Пример 7.1 Вычислим массу прямоугольного параллелепипеда |
|
||||
0 x a, |
0 y b, |
0 z c с плотностью x, y, z x y z |
|||
40
