metod1_KI_dlya_studentov

Московский государственный технический университет имени Н.Э. Баумана

Факультет «Фундаментальные науки» Кафедра «Математическая физика и вычислительная математика»

Б.Т. Добрица, И.В. Дубограй, О.В. Скуднева.

Кратные интегралы и их приложения.

Москва

1

Модуль 1.

Занятие 1. Определение двойного интеграла. Геометрический смысл двойного интеграла. Теорема существования. Свойства

двойного интеграла. Сведение двойного интеграла к повторному и вычисление его в декартовых координатах. 1.Определение двойного интеграла. Теорема о его

существовании.

i 1

Эта сумма называется интегральной .

Определение. Двойным интегралом f x, y d от функции f(x,y) по

D

области D называется предел интегральной суммы (1.1) при неограниченном возрастании числа разбиений n области D и стремлении наибольшего из диаметров разбиения к нулю (если этот предел существует).

Область D называется областью интегрирования.

Теорема существования двойного интеграла. Если функция f(x,y)

непрерывна в замкнутой ограниченной области D (с кусочно-гладкой границей), имеющей конечную площадь и диаметр, то она интегрируема по этой области, то есть существует предел интегральной суммы (1.1) при

n и max di 0 , не зависящий от способа разбиения D на элементарные области и от выбора точек Pi .

2

D , ограниченного цилиндрической поверхностью с образующей, параллельной оси OZ, и поверхностью z f x, y . См. рис. 1.2

Рассмотрим пример непосредственного вычисления двойного интеграла. Пример 1.1. Вычислим двойной интеграл по области D от функции z xy ,

0 y 1

если D : .

0 x 1

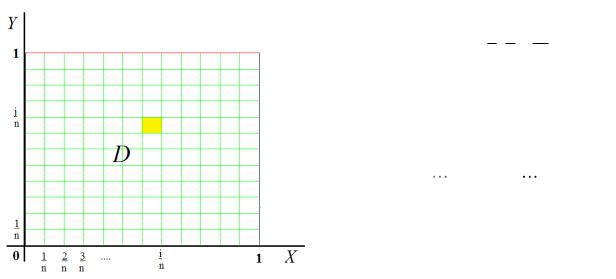
Решение. Разобьём квадрат на n2 частей. Тогда i 1n 1n n12 .

Выберем точки в правой верхней вершине каждого квадрата. (См.рис.1.3). Значение функции z xy в этих точках будет равно

По определению (см. (1.2)) имеем

Рис. 1.3

В подавляющем большинстве случаев вычисление пределов интегральных сумм представляет собой сложную и трудновыполнимую задачу. Для достижения результата эффективнее использовать повторный интеграл.

4. Повторный интеграл.

4

Область, ограниченная слева и справа прямыми

x x1 и x x2 , а сверху и снизу - кривыми y y1 x и y y2 x , такими, что любая прямая x x0 x1 x0 x 2 , проведённая через область D, пересекает каждую из кривых y y1 x и y y2 x в одной точке,

называется y-правильной. При этом точку А называют точкой входа в область, а точку В – точкой выхода из области.

(см.рис 1.4) То есть область D является y-

правильной, если

D x, y | x1 x x2 , y1 x y y2 x

Определив пределы изменения переменных по области D, расставляем пределы интегрирования в повторном интеграле:

Пример 1.3. Расставим двумя способами пределы интегирования в двойном

интеграле f x, y dxdy , где D – треугольник с вершинами O(0,0),

D

A(0,1),В(1,1).

Рисунок 1.5 Решение. Построим область D. Она одновременно является как

y-правильной, так и x-правильной. Поэтому первый способ расстановки пределов при переходе к повторному интегралу выглядит следующим образом.

Для всех точек данной области переменная x изменяется между x1 0 и x2 1, а переменная y для любого из этих x меняется

от y y1 x 0 до y y2 x x , т.е.

Рис. 1.6

6

D x, y | 0 x 1,0 y x .

Определив пределы изменения переменных по области D, расставляем пределы интегрирования в повторном интеграле:

Изменим порядок интегрирования, то есть расставим пределы интегрирования в повторном интеграле вторым способом (См.(1.4б)). Из рис. 1.6 следует, что для всех точек данной области переменная y

Пример 1.4. Изменим порядок интегрирования в повторном интеграле

Решение. Из данного интеграла следует, что область интегрирования ограничена прямыми x 0 , x 2 и кривыми y 2x x2 , y 2x .

Построим область D (См. рис. 1.7). Она является y-правильной, но не является x-правильной (См. рис .1.4). Для получения x-правильных областей придётся разбить область D на три части. Определим пределы, в которых меняются переменные по каждой из трёх областей для повторных интегралов

вида (1.4б).

0 y 1

D1 : y2 x 1 1 y2 ,4

7

Рис. 1.7

Занятие 2

Криволинейные координаты на плоскости. Замена переменных в двойном интеграле. Геометрический смысл модуля и знака Якобиана. Двойной интеграл в полярных координатах. Вычисление площади плоской фигуры с помощью двойного интеграла.

Ауд.: ОЛ-6 №№ 2160, 2162, 2164, 2166, 2171, 2177, 2183 или ОЛ-5 №№ 8.43,

44, 46, 48, 50, 56, 62.

1.Замена переменных в двойном интеграле.

Вычисление двойного интеграла может оказаться затруднительным, и тогда ищут другую систему координат, в которой интегрирование упростилось бы. При этом происходит преобразование переменных, а также и области интегрирования.

Рисунок 2.1

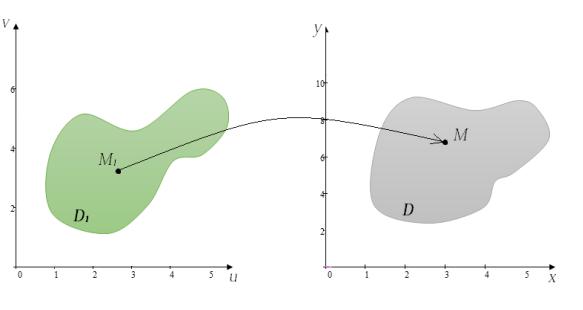
Пусть взаимно однозначное отображение области D' плоскости UOV

причём обе функции непрерывно дифференцируемы в области D' . (см. рис 2.1) При этом отображении площадь элементарной части

1i ui vi области D1 и площадь i xi yi соответствующей части

9