metod1_KI_dlya_studentov

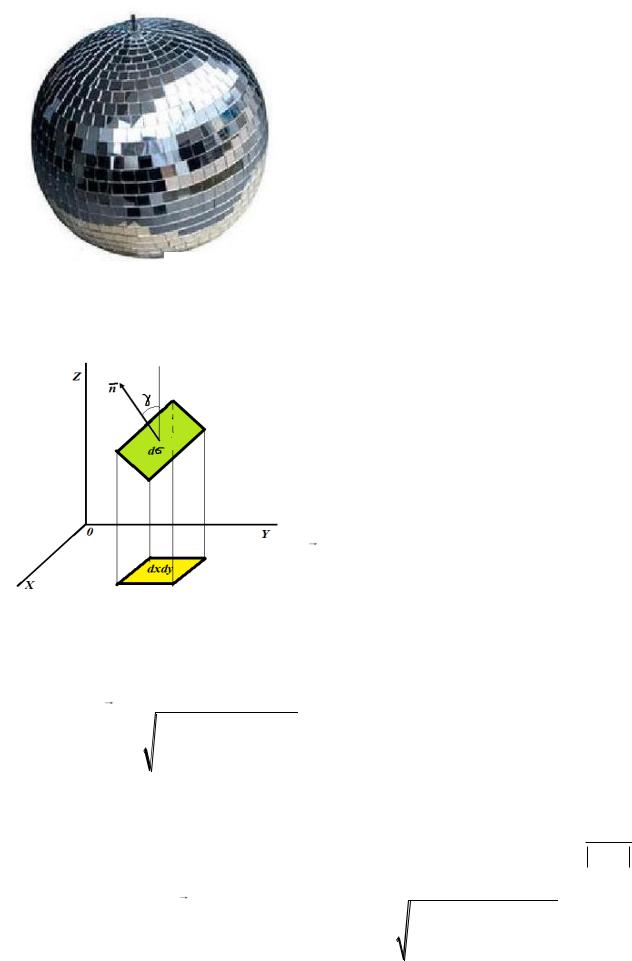
сумма площадей пластинок стремится к площади поверхности шара (см. рис. 3.7).

Рисунок 3.7

Пусть z f x, y - уравнение поверхности G и f x, y - непрерывная

дифференцируемая функция. Напомним, что каждый участок поверхности аппроксимируется участком касательной

нормированного вектора градиента

являются направляющими косинусами углов , , , которые градиент образует с осями координат.

21

части поверхности, которая однозначно проецируется в область D плоскости

Выберем способ его вычисления. В данном случае удобнее перейти к полярным координатам и учесть симметрию относительно плоскости XOZ . Половина области D1 является радиально правильной, где

22

Пример 3.5 В условиях предыдущего примера вычислим площадь боковой поверхности части цилиндра, заключённой между полусферой и плоскостью

XOY .

Решение. На рис. 3.10 зелёным цветом выделена половина заданной части цилиндра x2 y2 ax . Очевидно, что эта часть удобно, без наложения, проецируется только на координатную плоскость XOZ . Граница области D2 ,

в которую проецируется при этом зелёная часть цилиндра, состоит из трёх частей. Две из них очевидны, это x 0 и z 0. Третья часть является проекцией линии пересечения полусферы и цилиндра. Чтобы спроецировать линию пересечения на плоскость XOZ , необходимо построить проецирующий цилиндр, направляющей которого является эта линия, с образующей, параллельной оси OY . Уравнение этого цилиндра совпадёт с уравнением проекции линии пересечения двух поверхностей на плоскость

XOZ . (См. замечание 1)

Из системы уравнений

Эта формула получена из формулы (3.3), в которой роль функции играет y f x, z , а переменными интегрирования являются x и z .

23

Рисунок 3.11

Занятие 5.

Тройной интеграл. Определение тройного интеграла и его свойства. Формулировка теоремы существования тройного интеграла. Сведение тройного интеграла к повторному и его вычисление в декартовой системе координат.

1.Определение тройного интеграла.

Если существует предел последовательности этих сумм при условии, что количество разбиений неограниченно растёт, а максимальный из всех диаметров элементарных частей d стремится к нулю, то он называется

тройным интегралом по области V от функции f(x,y,z).

который не зависит от способа разбиения V на части и от выбора точек Pi .

3.Свойства тройного интеграла.

28

Свойства тройных интегралов аналогичны свойствам двойных интегралов от функций, непрерывных в рассматриваемых областях.

1.Линейность. Если функции интегрируемы по области V , то и их линейная комбинация интегрируема.

f1 x, y, z f2 x, y, z dxdydz

V

f1 x, y, z dxdydz f2 x, y, z dxdydz.

V V

2.Аддитивность. Если область V разбита на две области V1 и V2, не имеющие общих точек, то

f x, y, z dxdydz f x, y, z dxdydz f x, y, z dxdydz

Примечание. Свойства 1 и 2 верны для любого фиксированного числа слагаемых.

3.Сохранение знака. Если в области V f x, y, z 0 , то f x, y, z dV 0 .

V

4. Интегрирование неравенств . Если в области V f1 x, y, z f2 x, y, z ,

5.Для знакопеременной функции f(x,y,z) справедливо неравенство:

7.Теорема об оценке. Если функция интегрируема по области T и в этой области m f x, y, z M , то mV T f x, y, z dxdydz MV T , где

29

8.Теорема о среднем. Если функция f(x,y,z) непрерывна в замкнутой области V, то в этой области существует точка M , , , такая, что

f x, y, z dxdydz f , , V ,

V

где V – объем данной области.

4.Вычисление тройного интеграла.

Пусть замкнутая ограниченная область V проецируется на координатную

плоскость XOY в правильную область D и любая прямая, перпендикулярная этой области D , пересекает граничную поверхность области V в двух точках (одна нижняя и одна верхняя).

непрерывные функции в области Dxy . Такая область V называется

правильной.

Теорема. Если V - правильная область с кусочно-гладкой границей, f x, y, z - непрерывная функция, то тройной интеграл

Если область Dxy является y- правильной, то двойной интеграл в свою очередь сводится к повторному и

В тройном интеграле, так же, как в двойном можно менять порядок интегрирования.

Пример 5.1 (2240) Расставим пределы интегрирования в тройном интеграле,

f x, y, z dV f x, y, z dxdydz , где V – тетраэдр, ограниченный

Решение. Построим данные в условии плоскости и выделим тетраэдр, объём которого требуется вычислить (см. рис. (5.2)).

30