Методичка_Пределы (все части)

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный технический университет им. H.Э.Баумана

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

loga b = logc b

, получаем следствия второго замечательного предела:

.pdf

Скачиваний:

122

Добавлен:

23.03.2016

Размер:

8.48 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 74 5 6 7 > Следующая >>>

	x +3		x		∞	∞
Решение.	x +3				∞	.
	A = lim			=
	A = lim	x		=
	x→∞	x			∞

Получили комбинированную неопределенность. Избавимся сначала, используя

правило 1, от неопределенности ∞∞ .

		3	x	∞
A = lim 1	+			= [1	].
A = lim 1	+	x		= [1	].
x→∞		x

Преобразованное выражение при подстановке x = ∞ дает неопределенность , от которой можно избавиться, построив второй замечательный предел (См.

(3б)).

Сравнив наш предел с (3), видим, что роль α =α(x)

играет

И тогда

A = lim 1

= lim 1+

= lim 1

= e

x→∞

Ответ.

A = e3 .

Замечание. Рассмотренный в примере 25 предел позволяет сделать следующий вывод (следствие второго замечательного предела):

		k x		k	.	(4)
A = lim 1	+		= e

x→∞		x

Формула (4) останется справедливой, если заменить предел функции пределом последовательности.

Пример 26. Вычислим A = lim 5x + 2 x−2 .

x→2 3x + 6

.Решение. Подставим в функцию x = 2 :

A = lim 5x + 2 x−2 = [1∞ ]. x→2 3x + 6

Получили неопределенность, от которой можно избавиться, применив правило 5, т.е. выделив второй замечательный предел. Чтобы выяснить, что в данном примере играет роль α(x)→ 0 , преобразуем его следующим образом.

5x + 2

x−2

2x − 4

x−2

A = lim 1

−1

= lim 1

3x + 6

x→2

3x + 6

x→2

2x − 4

Теперь ясно, что при

x → 2

α(x)=

→ 0 . Продолжим построение

(1+α

)α с

3x + 6

полученным α(x)=

2x − 4

3x + 6

xlim→2

− 4

2x −

3x+6

2x−4

2x − 4

3x+6

−2

2x−4 3x+6

x−2

2x−4

= e12 .

A = lim 1+

3x + 6

= lim 1

3x +

= lim 1

3x + 6

x→2

Ответ.

A = e6 .

Пример 27. Вычислим

3x +1 x

= lim

3x −5

Решение.

x→∞

3x +1

∞

Воспользуемся

правилом 1,

чтобы избавиться от

A = lim

3x −5

∞

x→∞

неопределенности ∞

∞

3 +

1 x

3x +1

∞

A = lim

= lim

= [1

x→∞ 3x −5

x→∞

3 −

Далее применяем правило 5.

Заметим, что при x → ∞ числитель и знаменатель похожи на следствие второго замечательного предела (4).Исходя из этого, вынесем в числителе и знаменателе за скобку тройку и получим

1 x

1/ 3

lim 1+

A = lim

x→∞

= e3+

3 e2 .

−5 / 3 x

x→∞

1−

−

lim 1

x→∞

Ответ.

A = e2 .

πx

Пример

28.

Вычислите

(x−1)2

самостоятельно, отвечая

= lim sin

последовательно на вопросы.

x→1

Решение. 1) Что	получается при непосредственной подстановке x =1, ответ или
неопределенность?	(неопределенность типа [1∞ ])

2) Какое правило можно применить, чтобы избавиться от этой неопределенности? (правило 5)

3) Преобразуйте данное выражение так, чтобы в основании сложнопоказательной функции выделилось выражение (1+α).Что играет роль α(x)→ 0 ?

( α = sin π2x −1 )

4) Постройте второй замечательный предел. Как выглядит выражение после применения этого предела?

		sinπx −1
	lim	2
	( A = ex→1		(x−1)2 )
			sin πx −1
5) Рассмотрите отдельно	B = lim		2	.	Что получается при
5) Рассмотрите отдельно	B = lim		(x −1)2	.	Что получается при
непосредственной подстановке	x→1		(x −1)2
непосредственной подстановке	x =1, ответ или неопределенность, и какое
правило можно применить, чтобы избавиться от этой неопределенности?
((неопределенность типа 0					, правило 4)
				0

6) Что необходимо предпринять, чтобы в новом пределе выделить первый

замечательный предел?

(замену переменной x −1 = t → 0 )

7) Как будет выглядеть предел

после выбранного преобразования и что

получится после подстановки x −1 = t ?

π t

1−cos

( B = −lim

)

x→1

8)Что

можно

сделать для избавления от получившейся неопределенности?

(удобнее

всего

воспользоваться

следствием

первого

замечательного

предела,

(см.(2)), а именно lim

1−cosα = 1

при α =

π t

)

α→0

α2

и дайте

9)Преобразуйте необходимым образом выражение,

вычислите B

окончательный ответ.

( B = −π 2 , A = eB )

π 2

Ответ.

A = e−

8 .

Задачи для самостоятельной работы.

Вычислите следующие пределы.

13)

3x +1

ctgπx

A = lim

, 14)

, 15) A = lim

A = lim

−3

x→∞ 3x

−1

x→∞

x→1 x

16)

A = lim(cosπx)1/(

−2)2 ,

17) A = lim(cos

)1/ x .

x+2

x→2

x→0

Ответы. 13)0 , 14) e2 , 15) e−1/ 2π , 16) e−8π 2

, 17) e−1/ 2 .

Помимо формулы (4), существуют и другие следствия второго замечательного предела. Они будут выведены в следующих двух примерах.

Предварительно заметим, что если существует lim f (x)> 0 , то

x→

limloga f (x)= loga lim f (x) в силу непрерывности логарифма (теоремы 3 и 4).
x→	x→
Пример 29.	Вычислим	lg(1+ x)
		A = lim	x	.
		x→0
.Решение. Подставим в функцию			x = 0

	lg(1+ x)		0
A = lim			=		.
		x		0
x→0

Получили неопределенность, от которой нельзя избавиться известными нам способами из-за наличия в выражении логарифмической функции. Преобразуем данную функцию, используя свойство логарифмов k loga b = loga bk .

	lg(1+ x)			1			1		1	∞
A = lim			= lim		lg(1	+ x)= limlg(1		= lg lim(1		= lg[1 ].
		x		x			+ x)x		+ x)x
x→0			x→0			x→0		x→0

Получили выражение, содержащее второй замечательный предел. (см.3).

Теперь A = lg lim(1+ x)= lg e .

x→0

Ответ. A = lg e .

Замечание. Обобщая результат примера 29, в котором был использован второй замечательный предел, и учитывая еще одно свойство логарифмов

log	a	(1	+α)		1	.	(5)
lim				=
		α			ln a
α→0

Пример 30. Вычислим A = lim a x −1 .

x→0 x

.Решение. Подставим в функцию x = 0

		x	−1	0
	a
				=		.
A = lim			x		0
x→0

.Получили неопределенность, от которой нельзя избавиться известными нам способами из-за наличия в выражении показательной функции. Преобразуем выражение так, чтобы появилась возможность использовать какой-либо из уже разобранных приемов. Для этого заменим числитель новой переменной

a x −1 = t → 0 .

−1

= t

→ 0

= lim

A = lim

log

+t)

loga (1

+t)

x→0

t→0

= loga (1+t)

lim

t→0

Появилась возможность применить одно из следствий второго замечательного предела (см.5).

Замечание. Получили результат, который тоже является следствием второго замечательного предела:

−1

lim

= ln a

α→0

(6)

lim

eα

−1

α→0

Пример 31. Вычислим A = lim

5x −ex

log5 (x +5)−1

x→0

.Решение. Подставим в функцию

x = 0

A = lim

e5x −ex

= 0

log5 (x +5)−1

x→0

Преобразуем данное выражение, используя свойства показательной и логарифмической функций, и воспользуемся известными пределами (5) и (6).

A = lim

e5x −ex

= lim

ex (e4x −1)

= lime

lim

e4x −1

log5 (x +5)−log

5 5

5 + x

x→0

log5

x→0

log

Теперь в числителе можно построить предел (6)

при α = 4x , а в знаменателе

предел (5) при α =

A = lim

(e4x −1)4x

= lim1 4x

5ln 5

= 20ln 5 .

x→0

log

Ответ.

A = 20ln 5 .

Задачи для самостоятельной работы.

Вычислите следующие пределы.

(3x − 2)

18) A = lim x(ln(x +3)−ln x), 19)

log

, 20)

A = lim

e4x −e−4x

A = lim

x→+∞

x→1

x −1

x→0

21) A = lim

arcsin 4x

, 22)

A = lim(1−ln(1+ x3 ))3 / x2 arcsin x .

x→0 2x

−1

x→0

Ответы. 18) 3

, 19)

, 20)

, 21)

, 22) e−3 .

ln 2

ЧАСТЬ 4.ОДНОСТОРОННИЕ ПРЕДЕЛЫ ФУНКЦИИ.

Кроме

ранее

рассмотренных

вариантов

поведения функции при

x → возможны и другие.

4.1. Односторонние пределы функции при стремлении аргумента к бесконечно удаленной точке.

Функция может вести себя различным образом в зависимости от того, стремится ли аргумент к бесконечно удаленной точке (+ ∞) или (−∞). Например,

известная функция y = arctgx такова, что

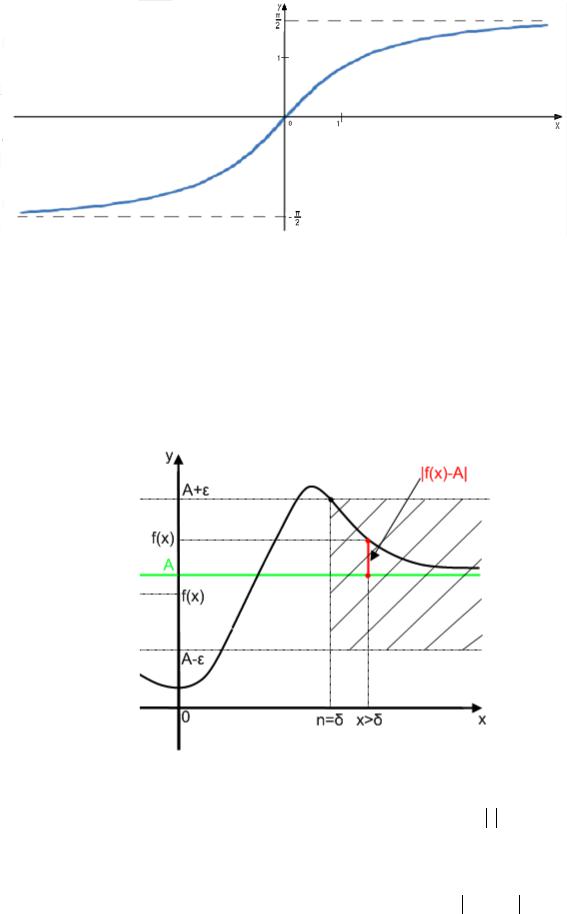
lim arctgx = π		,
x→+∞	2		Рис.14
		π
lim arctgx = −
x→−∞		2

Рассмотрим один из возможных вариантов поведения функции при стремлении аргумента к бесконечно удаленной точке и, используя результаты, полученные в части 2.3, сформулируем соответствующее определение.

Пусть при x → +∞ существует A = lim f (x).Рассмотрим геометрическую

x→+∞

интерпретацию, взяв правую часть рис.11.

Рис.15 Определение 5 остается в силе, но только для достаточно больших

положительных значений переменной x .Откуда следует, что x = x , т.к. x > 0. Определение 8. Число A называется пределом функции y = f (x) при x → +∞,

т.е. lim f (x)= A , если для любого ε > 0 найдется δ > 0, такое что для всех x ,

x→+∞

удовлетворяющих условию x > δ , выполняется неравенство f (x)− A < ε . Или в символах:

x = a , иллюстрация которого

def

• A = lim f (x)=

x→+∞

def

• A = lim f (x)=

x→+∞

ε>0		δ>0: x>δ		∞	ε	ε
ε	>0	δ	δ
		>0: x		\|f(x)-A\|< .
			Ů (+ )		f(x) U (A).

Рассмотрим теперь другой вариант. Пусть предел функции равен числу А при x → −∞,

Рис.16

Определение 7. Предел функции

y = f (x)

равен числу А при

x → −∞,

т.е.

lim f (x)= ∞ , если для любого ε > 0

найдется δ > 0 , такое что

для всех

x ,

x→−∞

f (x)− A

удовлетворяющих условию x < −δ , выполняется неравенство

< ε .

Или в символах.

•

def

>0: x<-

|f(x)-A|< .

A = lim f (x)=

x→−∞

ε>0

δ>0: x

Ůδ(- )

f(x) εU (A).

•

def

A = lim f (x)=

x→∞

∞

4.2.Определение односторонних пределов функции при x → a .

Рассмотрим поведение функции около точки приведена на рис. 17.

Число A , к которому стремится значение функции при приближении точки к x = a , слева, называется левосторонним пределом этой функции, а число B - ее правосторонним пределом.

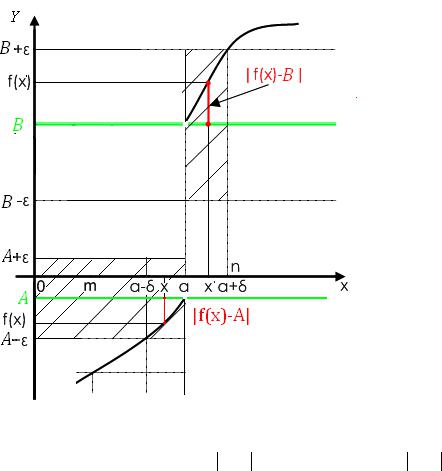
Рис. 17

Чтобы четко сформулировать определения этих пределов, возьмем за основу определение 4 и отметим, что x − a = x − a при x > a и x − a = a − x при x < a .

Определение 10.Число

называется

левосторонним пределом функции

y = f (x) при x → a −0 , если для любого ε > 0

найдется δ > 0 , такое что для всех x ,

удовлетворяющих условию a −δ < x < a , выполняется неравенство

f (x)− A

< ε .

Символическая запись:. A

x→a−0 f

def

ε>0 δ>0: а-δ<x<a |f(x)-A|<ε.

(

lim

Определение 11.Число

называется

правосторонним пределом функции

y = f (x) при x → a + 0 , если для любого ε 0

найдется δ(ε) 0 , такое что для всех

x , удовлетворяющих условию a x a +δ , выполняется неравенство									f (x)− A	ε .

	= lim		(		def	ε>0	δ>0: а<x<a+δ \|f(x)-A\|<ε.
Символическая запись:. A		f		x	)=
	x→a+0
Пример 32. Постройте	графическую иллюстрацию для lim							f (x)= −∞ и
							x→a−0

сформулируйте определение этого предела, отвечая последовательно на поставленные вопросы.

Решение.

1)Какой из приведенных в пособии рисунков ближе всего к требуемому? (Рис.12)

2)Как преобразовать исходный рисунок, чтобы получить требуемый? (Стереть часть рисунка справа от прямой х=а. Отразить то, что останется, относительно оси ОХ.)

3) По аналогии с каким из основных определений главы 2 можно дать определение для заданного в условии предела?

(Определение 6) 4) Чему в данном случае будет равен x − a ?

(

x − a

= a − x )

5) Чему в данном случае будет равен

f (

(

f (x)

= − f (x), т.к. f (x)< 0 )

6) Сформулируйте определение и запишите его в символах.

lim

def

ε>0

δ>0: а-δ<x<a -f(x)>ε.).

f (x)= −∞ =

( x→a−0

Вычисление односторонних пределов уже встретилось нам в примере 14. Приведем еще несколько примеров.

Пример 33а). Вычислим пределы функции

f (x)=

x2 + 4

2x +3

x → +∞.

x, x ≥ 0

Решение. Отметим, что

− x, x <

− x

+ 4

∞

Поэтому A =

lim

= lim

= −

x→−∞

∞

x→−∞

2 +

∞

B = lim

= lim

2x +3

x→+∞

∞

→+∞

2 +

Ответ.

A = −

, B =

1 .

Пример 33б). Вычислим односторонние пределы функции

при x → ±0 .

arctgx, x ≥ 0

Решение. Отметим, что

arctgx

− arctgx, x < 0

И тогда A = lim

= lim

− arctgx = −1,

(см.(2)).

arctgx

x→−0

→−0

B = lim

= lim arctgx =1.

x→+0

Ответ.

A = −1,

B =1.

при x → −∞ и

f (x)= arctgxx

Заметим, что в этих примерах двусторонних пределов нет.

Теорема 5 (о связи односторонних пределов с двусторонним)

Двусторонний предел существует тогда и только тогда, когда существуют оба односторонних предела, и они равны друг другу.

Задачи для самостоятельной работы. Дайте определения следующих пределов функции.

def

ε>0

δ>0: x < < f(xδ -

lim

f (x)= +∞.

Отв. A = lim f (x)=

>0: а-

x a

f(x)>

x→a−0

x→−∞

f(xε)>

x→+∞

f (x)= −∞.

x→−∞

f (x)

def

>δ

lim

Отв.

lim

= −∞ = ε

>0 δ

>0: аδ<x <a+

x→a+0

lim f (x)= +∞.

Отв.

lim

def

f (x)= −∞ =

Вычислите следующие односторонние пределы.

lim (

+ x)

Отв. A = −

(напоминание: при x<0 |x|=- x)

+ 7x −1

x→−∞

A = lim

, B

= lim

Отв. A = −∞, B = +∞

x2 −5x

+ 6

−5x + 6

→2−0

x→2+0 x2

A = lim

2 x

B = lim

2 x

Отв.

A = 0 , B =1

→−0 2 x −1

x→+0 2 x −1

5.ПРАВИЛОЛОПИТАЛЯ-БЕРНУЛЛИ.

При вычислении пределов, содержащих различные неопределенности, не всегда можно воспользоваться ранее разобранными правилами. Тогда при выполнении необходимых условий можно применить правило Лопиталя-

Бернулли.

Вэтой главе предполагается, что читатель уже знаком с таблицей производных

иправилами дифференцирования. Читатель может повторить этот материал по задачнику [Ефимов, т.1], начало главы 5.

ПРАВИЛО 6. Если функции	f (x)	и ϕ(x)				непрерывны и дифференцируемы в
окрестности точки x = , то lim	f (x)	=	0	,	∞	= lim	f ′(x)	. Т.е. предел отношения
	ϕ(x)		0		∞
							ϕ (x)
x→						x→	′

двух функций, стремящихся одновременно к нулю или к бесконечности, равен пределу отношения их производных (если последний существует).

Пример 34. Вычислим A = lim log2 x .

x→+∞ x

.Решение.	log		2	x		∞
	A = lim				=	.
		x
	x→+∞					∞

Получили неопределенность, от которой нельзя избавиться известными нам способами, применяя правила с 1-ого по 5-ое. Используем правило 6.

<<< < Предыдущая 1 2 34 / 74 5 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
09.02.2015895.51 Кб40Методичка ПТМ №27.docx
#
27.04.2019115.11 Кб4Методичка Технологическая карта.docx
#
13.08.20191.13 Mб24Методичка Численные методы решения дифур.doc
#
09.02.20152.47 Mб75МЕТОДИЧКА.doc
#
09.11.20195.63 Mб14Методичка_(версия_для_печати).doc
#
23.03.20168.48 Mб122Методичка_Пределы (все части).pdf
#
23.03.2016158.48 Кб24Методичка_Пределы_1_Оглавл.pdf
#
23.03.2016373.58 Кб8Методичка_Пределы_2_Предел_послед_и_Опр_пред_функц.pdf
#
23.03.2016312.03 Кб11Методичка_Пределы_4_Сравн_Функц.pdf
#
09.02.20156.67 Mб119Методички по физике 2 курс.doc
#
05.05.2019224.26 Кб0МетодУк_пр_зан_2012.doc