Проекции многогранников

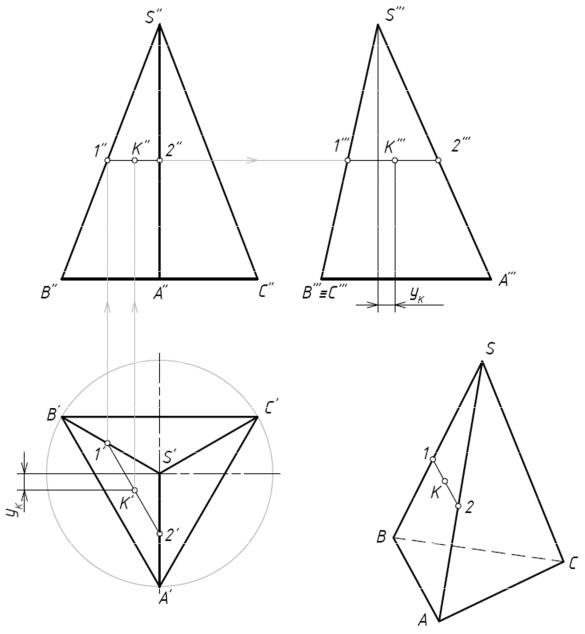
11

строим фронтальную проекцию 1ʹʹ2ʹʹи по линии связи найдемKʹʹ. Профильную проекцию

Kʹʹʹпостроим, проведя горизонтальную линию связи и определив координату уК точкиK.

Рис. 3

Оглавление

Т.Л. Белобородова, Е.Ю. Кичигина. Проекции многогранников.

12

Пересечение пирамиды проецирующей плоскостью

Задача 1

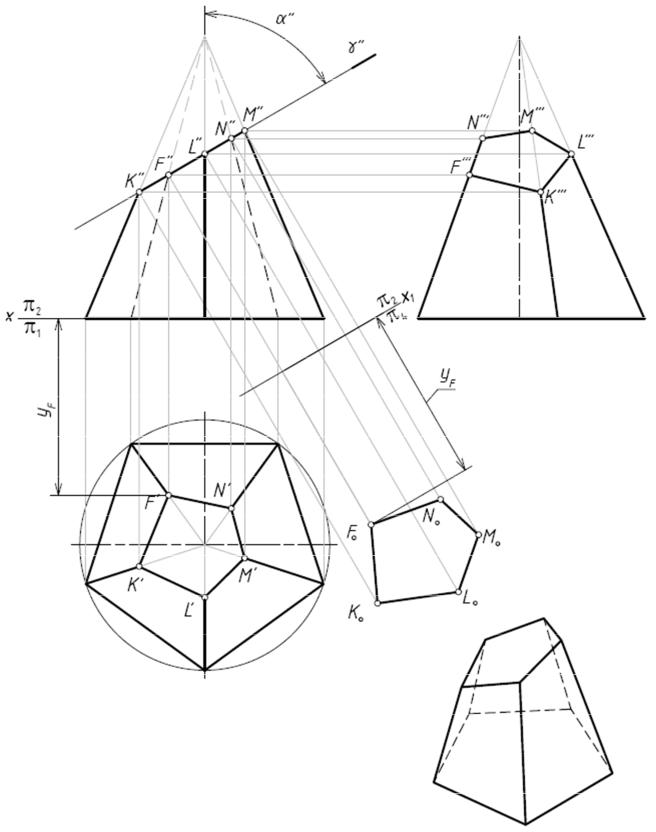
Рассмотрим построение проекций правильной пятиугольной пирамиды, усеченной фронтально-проецирующей плоскостьюγ, наклоненной к оси пирамиды под углом α° (Рис.4).

Секущая плоскость пересекает ребра пирамиды в точках K, L, M, N, F, а боковые грани по прямым, соединяющим эти точки. Сечением пирамиды плоскостью γ является пятиуголь-

ник, проекция которого на фронтальную плоскость есть прямаяKʹʹMʹʹ, совпадающая с фрон-

тальной проекцией плоскости γ. Проекция сечения на горизонтальную плоскость – пяти-

угольник Kʹ, Lʹ,Mʹ,Nʹ,Fʹ, вершины которого принадлежат соответствующим ребрам и нахо-

дятся с помощью вертикальных линий связи. Проекция сечения на профильную плоскость – пятиугольникKʹʹʹLʹʹʹMʹʹʹNʹʹʹFʹʹʹ, вершины которого находятся с помощью горизонтальных линий связи. Истинный вид пятиугольника сечения построим способом замены плоскостей проекций.

Рассмотрим подробнее это построение. Введем плоскость проекций π4, параллельную плоскости сечения γ на произвольном расстоянии от нее. Таким образом, получим новую систему плоскостей π2 /π4, в которой не изменилось положение плоскости π2 , а, следователь-

но, остались неизменными координаты у.

Через фронтальные проекции точек Kʹʹ,Lʹʹ,Mʹʹ,Nʹʹ,Fʹʹпроводим линии связи, перпенди-

кулярные оси х1. На этих линиях связи от оси x1 откладываем расстояния, равные расстояни-

ям от оси x до горизонтальных проекций точек Kʹ, Lʹ,Mʹ,Nʹ,Fʹ исходной системы, т.е. коорди-

наты у этих точек.

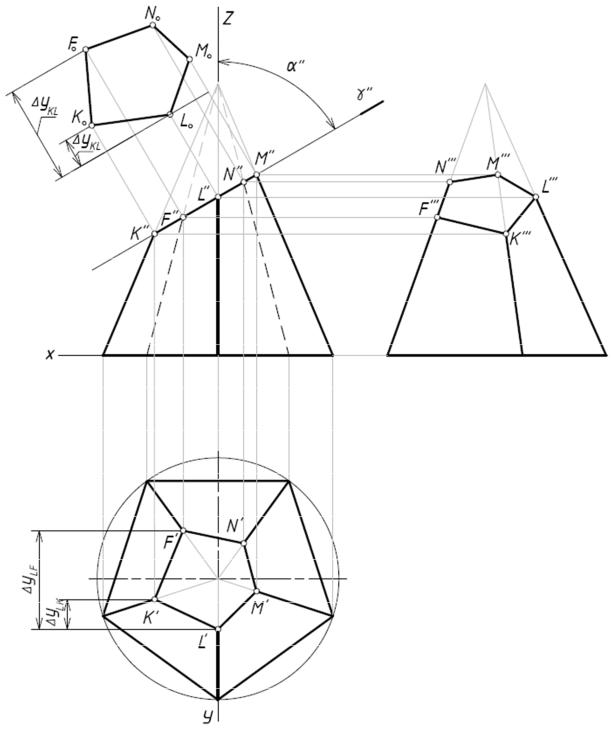
Построение истинного вида пятиугольника сечения можно выполнить, не используя оси проекций, а используя разности координат у (Рис. 4а). Построение при этом можно выполнить в любом месте, откладывая разности координат (в данном случае ∆у) на прямых линиях,

перпендикулярных проекции плоскостиγʹʹ.

Оглавление

Т.Л. Белобородова, Е.Ю. Кичигина. Проекции многогранников.

13

Рис. 4

Оглавление

Т.Л. Белобородова, Е.Ю. Кичигина. Проекции многогранников.

14

Рис. 4а

Оглавление

Т.Л. Белобородова, Е.Ю. Кичигина. Проекции многогранников.

15

Задача 2

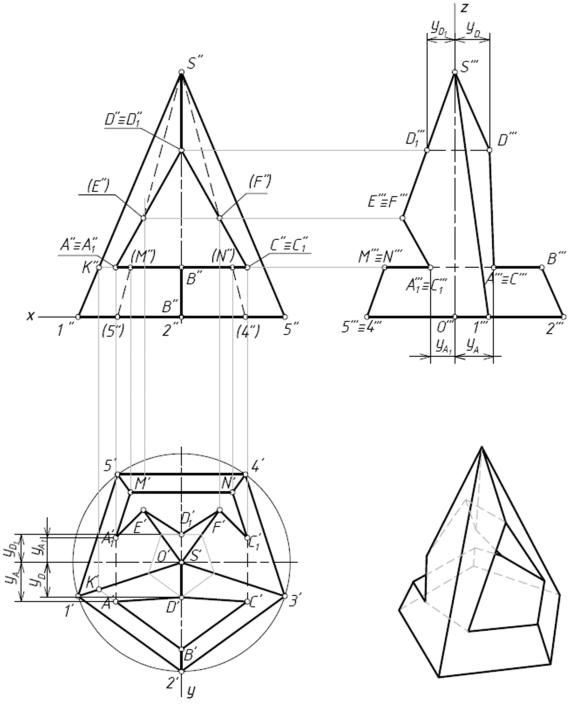
Рассмотрим пример построения проекций пирамиды со сквозным отверстием, обра-

зованным фронтально проецирующими плоскостями (Рис. 5). Задача сводится к построе-

нию линий пересечения плоскостей, одна из которых занимает проецирующее положение.

Плоскости отверстия пересекают ребра в точках, а грани – по прямым, соединяющим эти точки. Так как плоскости отверстия перпендикулярны фронтальной плоскости проекции, то фронтальная проекция линии пересечения совпадает со сторонами треугольника.

Построим горизонтальную проекцию. Горизонтальная плоскость отверстия парал-

лельна основанию пирамиды, поэтому и горизонтальные проекции линий пересечения этой плоскости с гранями пирамиды параллельны соответствующим сторонам основания пира-

миды. Горизонтальные проекции этих линий пересечения построены с помощью точки К и

вертикальных линий связи. Плоскости треугольного отверстия пересекают рёбра пирамиды в точках B, D1, M, N, E, F. Горизонтальные проекции всех точек, кроме точки D1, построим с помощью вертикальных линий связи.

Горизонтальную проекцию точки D1, а также точки Dпостроим, используя горизон-

тали соответствующих плоскостей, с помощью точек LиL1 соответственно.

Построения завершим, соединив проекции точекAʹ,Bʹ, Cʹ,Dʹ, Aʹи точек A1ʹ,Mʹ, Nʹ, C1ʹ, Fʹ, D1ʹ, Eʹ, A1ʹи удалив часть ребра между точками Dʹ иBʹ.

Построим профильную проекцию.

Заметим, что грань S45 – профильно-проецирующая плоскость, профильные проек-

ции точек D1, M, N, E, F, лежащих в этой плоскости, проецируются на прямую

Sʹʹʹ5ʹʹʹ=4ʹʹʹ(профильную проекцию плоскости S45).

Точки BʹʹʹиDʹʹʹ находим с помощью горизонтальных линий связи до пересечения с профильной проекцией ребра S2. Профильные проекции точекA, A1, C, C1получим, опреде-

лив координаты этих точек (принимаем при этом за начало координат основание высоты пирамиды – точка О) и отложив их на горизонтальных линиях связи.

Для нахождения горизонтальных проекций точек Dи D1 можно использовать исполь-

зуем профильные проекции этих точекDʹʹʹ,D1ʹʹʹ. Горизонтальные проекции находим с по-

мощью вертикальных линий связи, определив координаты у этих точек.

Соединяем полученные проекции точек и удаляем часть ребра между точками Bʹʹʹ, Dʹʹʹ и часть грани между точками Mʹʹʹ=Nʹʹʹ, Eʹʹʹ=Fʹʹʹ.

Проводим все линии невидимого контура.

Оглавление

Т.Л. Белобородова, Е.Ю. Кичигина. Проекции многогранников.

16

Рис. 5

Оглавление

Т.Л. Белобородова, Е.Ю. Кичигина. Проекции многогранников.

17

Построение разрезов

Задача 3

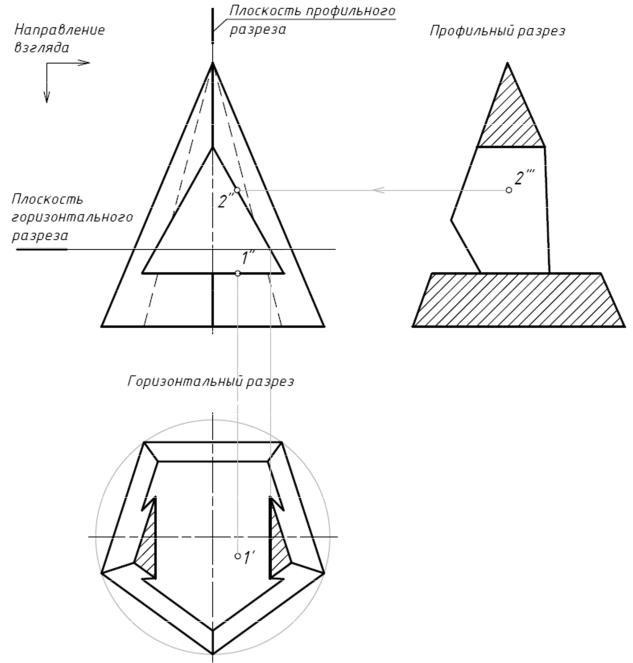
Для того, чтобы сделать видимыми внутренние поверхности отверстия в пирамиде, выпол-

ним разрезы (Рис. 6). Горизонтальный разрез выполняем плоскостью, параллельной гори-

зонтальной плоскости проекций, и строим его на месте горизонтальной проекции пирами-

ды. Часть пирамиды, расположенная выше этой плоскости, мысленно удаляют.

Рис. 6

Оглавление

Т.Л. Белобородова, Е.Ю. Кичигина. Проекции многогранников.

18

Таким образом, горизонтальная плоскость отверстия стала видимой. Точка 1 рас-

полагается на этой плоскости. Заштрихованы фигуры, по которым плоскость разреза разде-

лила пирамиду. Профильный разрез выполнен плоскостью, которая является плоскостью симметрии пирамиды и параллельна профильной плоскости проекций. Строим разрез на месте профильной проекции пирамиды. Половину пирамиды, расположенную перед плос-

костью разреза, мысленно удаляем. На профильном разрезе стала видна боковая плоскость отверстия, точка 2 принадлежит этой плоскости, теперь она видна. Заштрихованы фигуры,

по которым разделены части пирамиды.

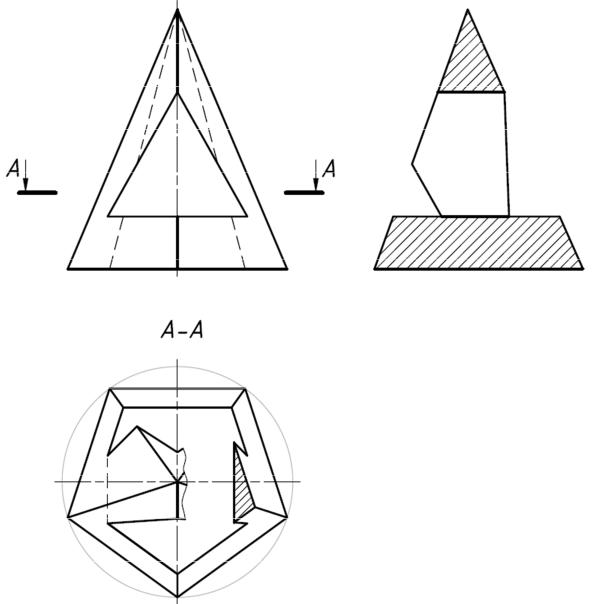
С учетом правил стандарта ГОСТ 2.305-2008 «Изображения – виды, разрезы, сече-

ния» по выполнению и обозначению разрезов выполним чертеж правильной пятиугольной пирамиды (рис. 7).

Рис. 7

Оглавление

Т.Л. Белобородова, Е.Ю. Кичигина. Проекции многогранников.

19

Чертеж содержит главный вид, горизонтальный разрез А-А, совмещенный с видом сверху (так как и вид сверху, и горизонтальный разрез являются симметричными фигура-

ми) и профильный разрез. Границей вида сверху и горизонтального разреза служит сплош-

ная волнистая линия, расположенная правее оси симметрии изображения. Это сделано для того, чтобы границей между разрезом и видом не оказалась линия контура. Согласно пра-

вилам стандарта границей между разрезом и видом должна быть или линия осевая или ли-

ния обрыва.

В отличие от горизонтального разреза профильный разрез не обозначен, так как се-

кущая плоскость профильного разреза совпадает с плоскостью симметрии фигуры.

Оглавление

Т.Л. Белобородова, Е.Ю. Кичигина. Проекции многогранников.

20

Заключение

Решение представленных домашних задач дает возможность перейти к рассмотрению более сложных задач на построение изображений по стандартам ЕСКД в курсе «Инженерная графика».

Вопросы для самоконтроля

1.Что называется многогранником?

2.Как проецируется плоскость, если она перпендикулярна плоскости проекций?

3.Какие признаки указывают на то, что на чертеже изображена призма, пирамида?

4.Какая призма (пирамида) называется правильной, прямой?

5.Какое изображение называется видом, разрезом, сечением?

6.Сформулируйте общее правило построения проекций точки, принадлежащей плоскости.

7.Поясните последовательность построения изображений способом замены плоскостей проекций.

Оглавление

Т.Л. Белобородова, Е.Ю. Кичигина. Проекции многогранников.