
6-1-воротников
.pdf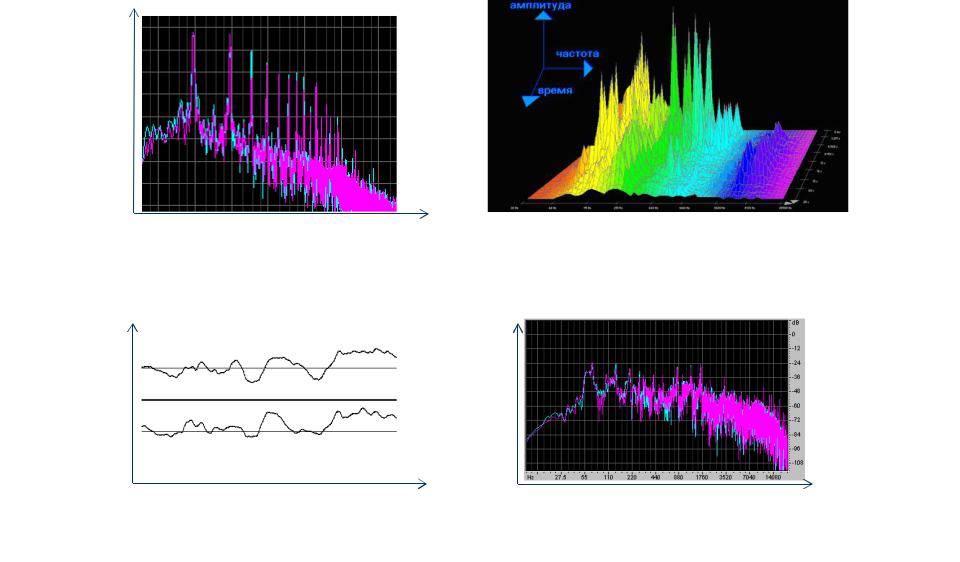
Элементы спектрального анализа
Спектр звука – это график зависимости его амплитуды от частоты (рис. 33, а).
Сонограмма (спектрограмма) – это изображение, показывающее зависимость спектральной
плотности мощности сигнала от времени (рис. 33, б). Применяется для идентификации речи, анализа звуков и в других областях.
Амплитуда
а |
Частота |
б |
|
||
Рис. 33. |
Спектр сигнала (а ) и его сонограмма (б ) |
|
Спектральная плотность мощности – это функция, задающая распределение мощности сигнала
по частотам.
Амплитуда |
|
Амплитуда |
|
а |
Время |
б |
Частота |
Рис. 34. Стереозапись мелодии (а ) и и ее спектр (б ) |
|
||
|
|
|
|
Локационные системы роботов |
Способы записи и анализа звука |
|
|
Динамическая спектрограмма
Динамическая спектрограмма в каждый момент времени показывает громкости (мощности)
составляющих звук тонов.
Анализ звукового сигнала осуществляется с помощью следующих устройств:
анализатора частот;
динамического спектрографа (сонографа).
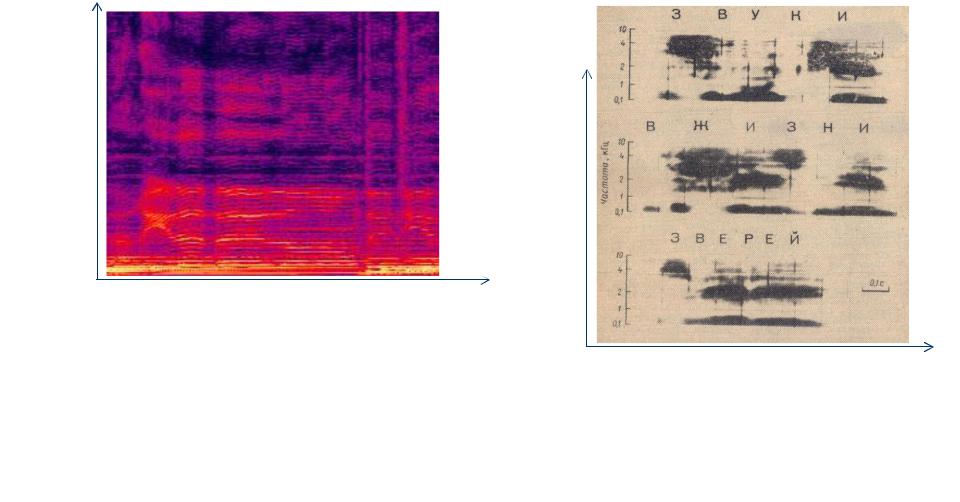
Интенсивность звука показана на динамической спектрограмме степенью затемнения (рис. 35, а,
б).
Частота Частота
а |
Время |
|
б |
Время |
Рис. 35. Пример спектрограммы сигнала (а), динамическая спектрограмма текста (б)
Спектральная плотность мощности имеет размерность мощности деленной на частоту, т.е.
энергии.
Локационные системы роботов |
Особенности распространения звука |

Спектрограмма голоса Марии Каллас (до STFT)
Локационные системы роботов |
Модуляция сигналов |
Оконное преобразование Фурье
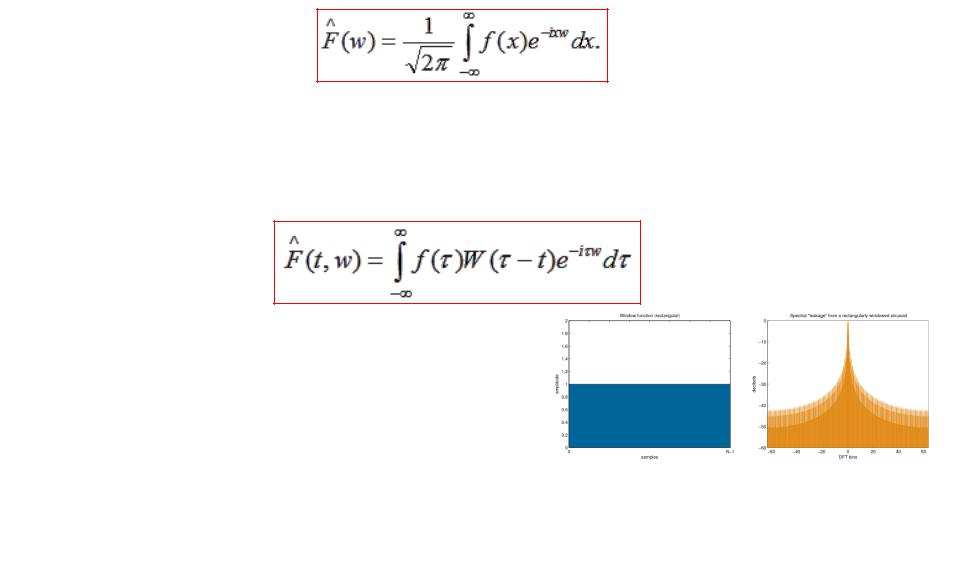
Математической основой спектрального анализа является преобразование Фурье, которое
связывает пространственный или временной сигнал с его представлением в частотной области.
Преобразование Фурье функции f (x) является интегральным представлением и задается следующей формулой:
Недостатком преобразования Фурье является то, что оно дает информацию только про частоту
сигнала и не дает никаких данных про то, в какой промежуток времени эта частота присутствует в сигнале.
Другим инструментом спектрального анализа является оконное преобразование Фурье (Shorttime Fourier transform), которое является разновидностью преобразования Фурье и определяется
следующим образом:
где W ( -t) — некоторая оконная функция. Обычно в
качестве оконной функции используется прямоугольное
окно (рис. 36, а), окно Гаусса, окно Хемминга, окно Ханна или окно Кайзера.
Результатом |
оконного |
преобразования |
Фурье |
|
|
|
является не |
спектр исходного сигнала, а |
спектр |
а |
|
||
произведения сигнала и оконной функции (рис. 36, |
б |
|||||
|
||||||
б). |
|
|
Рис. 36. |
Функция прямоугольного окна (а), |
||
|
|
|
спектр свертки синусоидального сигнала с |
|||
|
|
|
прямоугольным окном (б) |
|
||
|
|
|
|
|||
|
Локационные системы роботов |
Особенности распространения звука |
|
|||
Примеры преобразования Фурье
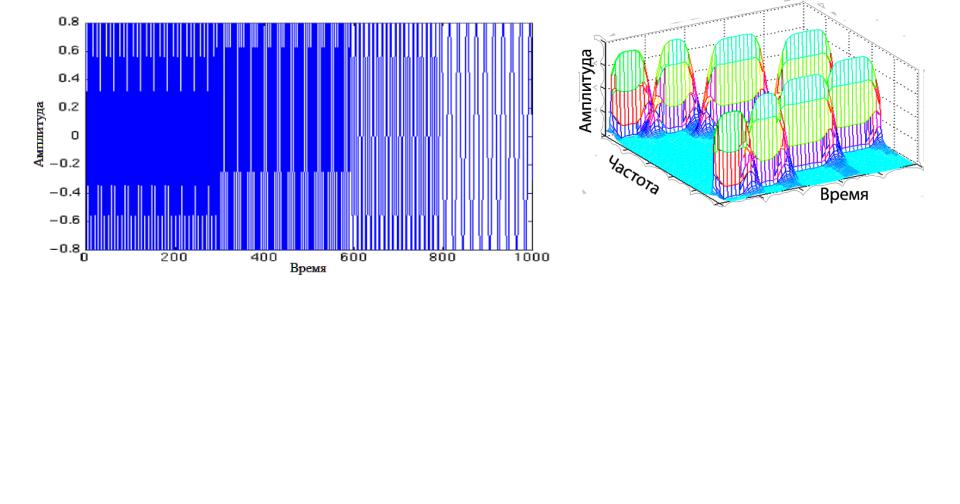
Рассмотрим следующий нестационарный сигнал (рис. 37, а). Его можно считать стационарным на
участках по 250 мс (на первом отрезке он имеет частоту 300 Гц, на втором — 200 Гц, на третьем —
100 Гц и на четвертом — 50 Гц).
Трехмерный (время, частота и амплитуда) график оконного преобразования Фурье будет иметь следующий вид (рис. 37, б). На трехмерном графике присутствуют четыре ярко выраженных максимума, которые соответствуют частотам, присутствующим в сигнале.
б
а
Рис. 37. Пример спектра нестационарного сигнала (а), график оконного преобразования Фурье (б)
Главной проблемой в использовании оконного преобразования Фурье является принцип
неопределенности Гейзенберга, который возникает для параметров времени и частоты сигнала.
Невозможно сказать точно какая частота присутствует в сигнале в данный момент времени (можно говорить только про диапазон частот) и невозможно сказать в какой точно момент времени частота присутствует в сигнале (можно говорить лишь про период времени).
Локационные системы роботов |
Особенности распространения звука |
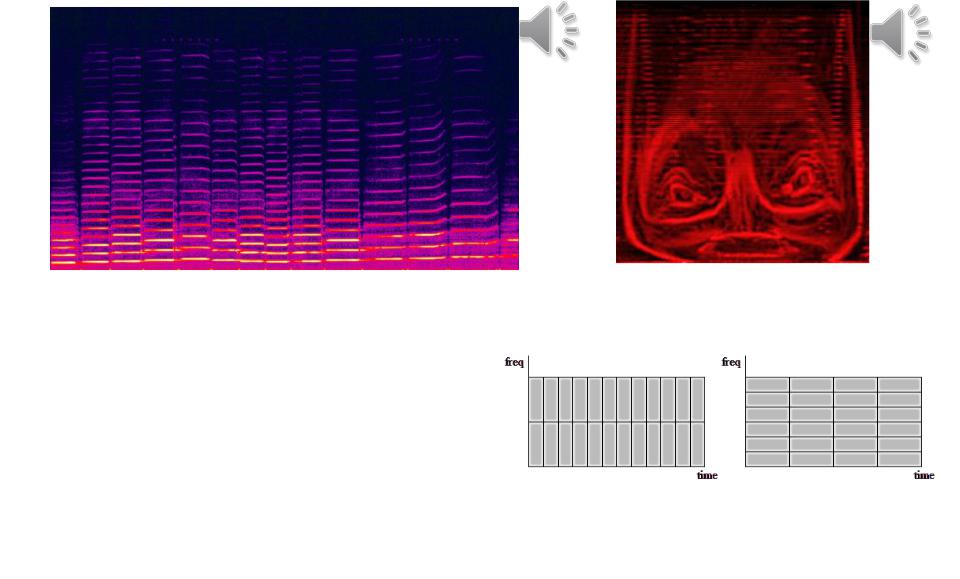
«Оконное преобразование» звука
Сонограмма представляет собой развертку спектра сигнала во времени (рис. 38). Поскольку каждый звук характеризуется спектром, сонограмма является полной характеристикой длящегося звукового сигнала.
а |
б |
Рис. 38. Сонограмма звуков: скрипки (а), синтезированного сигнала (б)
При построении сонограммы звука используют |
|
|
|
|
|
оконное преобразование Фурье, при котором |
|
|
|
|
|
сигнал анализируют на конечном временном |
|
|
|
|
|
интервале. |
|
|
|
|
|
В таком случае невозможно одновременно |
|
|
|
|
|
обеспечить хорошее разрешение по времени и |
|
|
|
|
|
|
|
|
|
|
|
по частоте (рис. 39). Чем уже окно, тем выше |
|
|
|
Ширина окна |
|
|
|
|
|
||
разрешение по времени и ниже разрешение по |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
частоте (принцип неопределенности). |
Рис. 39. Иллюстрация оконного преобразования Фурье |
||||
|
|
|
|
|
|
Локационные системы роботов |
Особенности распространения звука |
||||
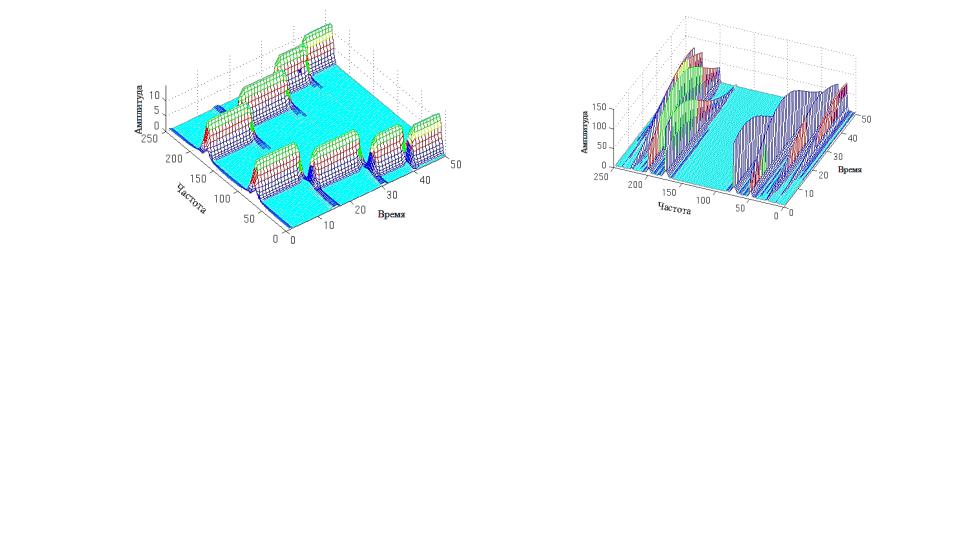
Разрешающая способность оконного преобразования
Разрешающую способность оконного преобразования Фурье можно регулировать с помощью
ширины окна.
Так, преобразования с узким окном в форме Гауссиана с масштабом (обратная величина к
ширине окна) 0.01 имеет следующий вид (рис. 40, а). Преобразование имеет хорошую точность по времени и плохую точностью по частоте (каждый максимум занимает некоторый диапазон частот).
а |
б |
Рис. 40. Оконные преобразования Фурье: с узким окном (а), с широким окном (б)
При использовании более широкого окна в форме Гаусианна с масштабом 0.00001 оконное
преобразование будет иметь вид (рис. 40, б). В данном случае мы получаем высокую точность относительно частоты, но при этом очень низкую точность относительно времени.
Можно считать, что обычное преобразование Фурье является оконным преобразованием Фурье с окном шириной в бесконечность.
Таким образом, при увеличении ширины окна (уменьшении его разрешающей способности) мы
увеличиваем точность относительно частоты и уменьшаем точность относительно времени. Значения ширины окна, при которой достигается оптимальное соотношение точностей находится методами вейвлет-преобразования.
Локационные системы роботов |
Особенности распространения звука |
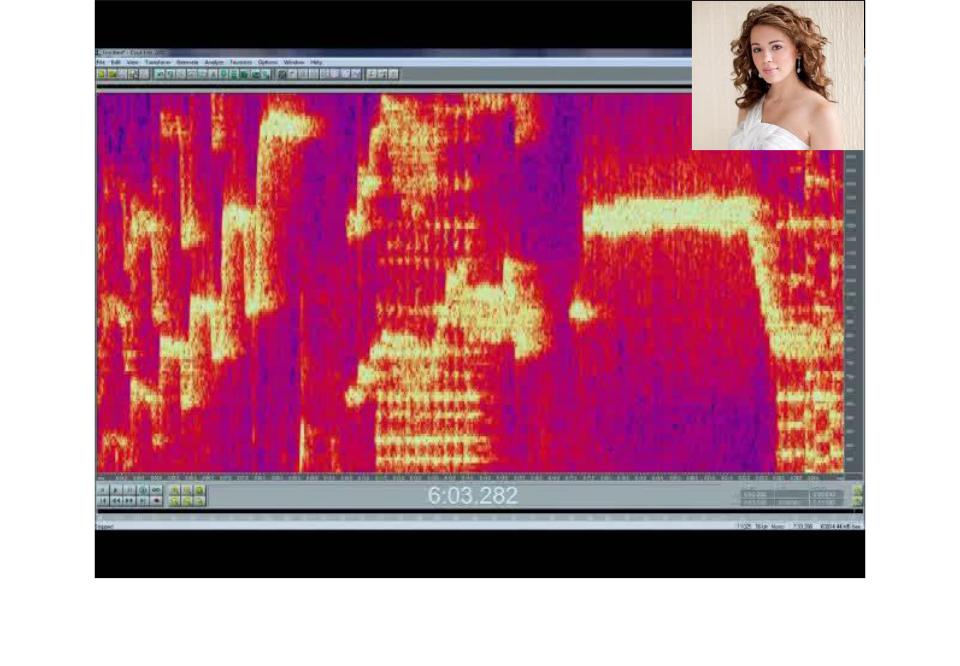
Спектрограмма голоса Рейчел Гилмор (после STFT)
Локационные системы роботов |
Модуляция сигналов |

Спектрограмма песни Beatles «All You Need Is Love»
Локационные системы роботов |
Модуляция сигналов |
Законы распространения звука
|
отражения и преломления |
дифракции и рассеяния звука |
закон волноводного |
|||||||||||
|
звука на границах сред |
|
при наличии препятствий |
распространения в |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ограниченных участках |
|
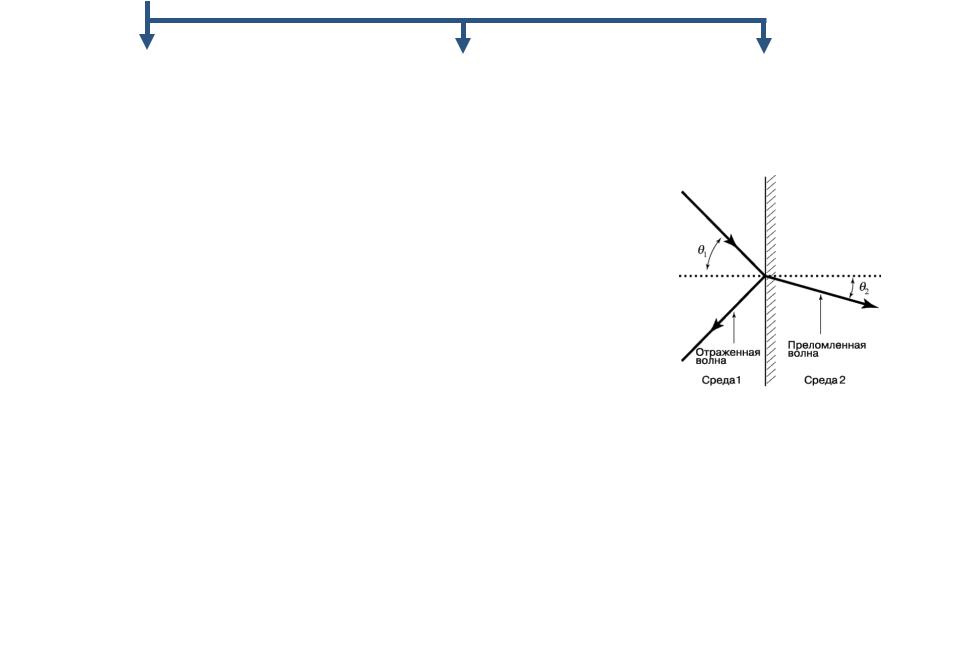
В звуковой локации наиболее важен закон Снеллиуса — закон отражения и преломления |
|||||||||||||
звуковых волн (рис. 41): |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
1 |
|
c |
|
|
sin |
|
|
|
|
|
|
|
|
|
|
1 |
|
или |
|
|
|
const, |
|
|
|
|
|
|
sin 2 |
c2 |
|
c |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|||||||||||
где 1 и 2 — соответственно угол падения и угол преломления, |
|
|||||||||||||
c1 |
и c2 — скорости распространения волн в первой и второй |
|
||||||||||||
средах. |
|
|
|
|
|
|
|
|
|
|
|
|||
При 1 > arcsin c1/c2 возникает полное внутреннее отражение (падающий луч полностью отражается от границы раздела сред).
Интенсивность звука при отражении и прохождении зависит от акустического импеданса и угла падения волны.
Рис. 41. Прохождение волны на границе двух сред
Коэффициенты отражения и прохождения звуковой волны определяются выражениями:
|
Jотр |
|
c |
c |
2 |
|
Z |
|
Z |
2 |
|
|
Jпр |
|
4 c |
c |
|
|
|
4Z Z |
2 |
|
|
|
kотр |
|
|
2 2 |
1 1 |
|
|
|
2 |
1 |
, |
kпр |
|
1 1 |
2 2 |
|
|
1 |
|
|
, |
||||
Jпад |
2c2 |
1c1 |
Z1 Z2 |
Jпад |
1c1 2c2 |
|
2 |
Z1 Z2 |
|
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
где J — интенсивности соответствующих волн, 1 |
и |
2, Z1 |
и |
Z2 — |
плотности и волновые |
|||||||||||||||||||
сопротивления материалов сред, соответственно. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Локационные системы роботов |
Особенности распространения звука |
