Выводы (по резонансу в шд):

При работе двигателя с номинальными токам наблюдается потеря устойчивости из-за резонанса на широкой полосе частот (39-47 Гц и 67-115 Гц). Для борьбы с резонансом был выбран метод: использование микрошагового режима, по следующим причинам:

1. Метод считается наиболее эффективным в решении проблемы резонанса в ШД.

2. При дроблении шага одновременно получаем более точное позиционирование ротора – что увеличивает точность системы.

3. Не требуется вносить каких-либо конструктивных изменений.

Анализ показал, что в ¼-шаговом режиме исчезает зона неустойчивости, влияние резонанса сильно уменьшилось, по сравнению с полношаговым режимом. Но наблюдается потеря точности на частоте 22-24 Гц, поэтому следует избегать подачу управляющего сигнала на ШД с этой частой.

Примечание: для ускорения вычислений к обмоткам был подключён добавочный резистор, чтобы стабилизировать ток в обмотках без использования ШИМ. Поэтому требуется дополнительно провести анализ динамики изменения тока в обмотках.

2.7 Форсирование тока в обмотках.

Индуктивность обмоток определяет время нарастания и спада тока. Поэтому если к обмотке приложено напряжение прямоугольной формы, форма тока не будет прямоугольной. При низких скоростях (рис. 16а) время нарастания и спада тока не способно сильно повлиять на момент, однако на высоких скоростях момент падает. Связано это с тем, что на высоких скоростях ток в обмотках двигателя не успевает достигнуть номинального значения (рис. 16б).

Рис. 2.7.1. Форма тока в обмотках двигателя на разных скоростях работы.

Для того, чтобы момент падал как можно меньше, необходимо обеспечить высокую скорость нарастания тока в обмотках двигателя, что достигается различными методами при использовании ШИМ:

1. Подключение добавочного сопротивления к обмоткам. При этом нужно увеличивать максимальный уровень ШИМа. При полном увеличении добавочного сопротивления до уровня ШИМ равным 100% источник напряжения практически превращается в источник тока и скорость изменения тока в обмотках значительно увеличивается, ценой падения КПД.

2. Программные методы. Эти методы предполагаю сохранение КПД, а вся корректировка управляющего сигнала находиться в микроконтроллере. Здесь возможны 2 подметода:

   1. Проводиться синтез корректирующего устройства, которое в дискретной форме вноситься в микроконтроллер.

   2. Импульсное форсирование. В начале каждого шага подаётся 100% - шим того или иного знака, иначе говоря импульс напряжения (в дальнейшем будем называть его форсирующий импульс), который приводит к быстрому изменению тока.

Следует рассмотреть все эти методы, чтобы выявить наилучший.

Для полноценного анализа создадим модель, которая будет иметь обмотку со всеми её параметрами, и логической схемой которая будет выводить время, когда ток достигнет уровня Inom с 5%-й погрешностью. Данную модель вы можете посмотреть в файле steping_motors_v8_p, сохраненный на диске:

Рис. 2.7.2

Желаемый результат.

Какое время нарастания мы будем считать приемлемым. По проведённому ранее анализу было решено использовать режим микрошага с делением шага 1/4 . (Далее 1/4-шаговый режим). Требуемая скорость по техническому заданию 70 мм/сек. С запасом возьмём 75 мм/сек. Переведём в шаги за секунду (из расчёта того что один шаг соответствует 0.236мм): получаем 75/0.236 = 318 шагов в секунду. Следовательно частота изменений тока в процессе работы будет в 4 раза больше: 318*4 = 1272 импульсов в секунду. Период изменения тока 1/1272 = 786 мкс. Это минимальное время, за которое ток должен достичь требуемого уровня (с некоторой погрешностью разумеется), потому что в противном случае момент ШД начнёт сильно снижаться. На практике даже уложиться в это время недостаточно, нужно в несколько раз быстрее делать спад/нарастание тока. Поэтому формируется следующее требование к скорости измения тока: чем быстрее тем лучше, но не менее 780 мкс.

Время нарастания без коррекции.

На вход обмотки подаём ШИМ с такой скважностью (Kd), чтобы получить установившееся значение тока 2.8 ампер:

Рис. 2.7.3

В результате получаем время возрастания тока 7121 мкс. Что крайне неудовлетворительно, применительно к тем требованиям, которые были сформулированы ранее.

Рис. 2.7.4.

Необходима коррекция, для увеличения скорости изменения тока в обмотке.

Использование добавочного сопротивления.

Посмотрим, каких результатов можно добиться подключив добавочное сопротивление. Возьмём крайний случай, использовав максимальное значение сопротивления для номинального тока. Оно вычисляется по формуле (21) и было получено во время исследования резонанса (7.67 Ом). Кроме того само это исследование базировалось на этом методе форсирования токов добавочным сопротивлением.

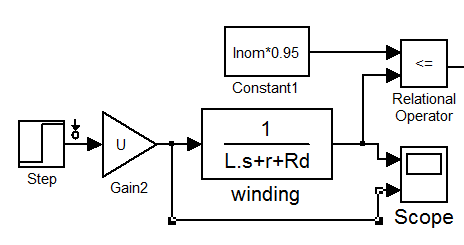
Рис. 2.7.5.

Схема заметно упростилась, потому что уровень ШИМа равен 100%, и поэтому драйвер не нужен вовсе. Время нарастания составляет теперь 870 мкс, что на порядок больше прошлого результата, но не подходит по требованиям к системе. На графике масштабирование шкалы времени осталось прежним, чтобы можно было сравнить с Рис. 2.7.4.

Рис. 2.7.6.

Следует заметить, что метод весьма неэкономичен. Поскольку на каждом двигателе находиться по 2 резистора с сопротивлением 7,67 Ома. И по каждому течёт ток 2.8 ампера. Следовательно тепловые потери на резисторах огромны: 2*7,67*2.8*2.8 = 120 Вт. Это сравнимо с мощным паяльником или среднестатистическим феном для волос. Причём данная мощность выделяется при питании одного двигателя, который сам потребляет около 60 Вт.

Корректирующие устройство в форме передаточной функции.

Требуется провести синтез системы, с целью добиться быстродействия. В начале построим ЛАЧХ неизменяемой части, то есть обмотки. У неё передаточная функция:

Для построения ЛАЧХ делаем входы и выходы из передаточной функции:

Далее заходим в меню Tools -> Control Design -> Linear Analysis… и производим линеаризацию модели:

Рис. 2.7.7.

Здесь нужно поднять амплитуду на средних частотах, когда отставание по фазе составляет 45 градусов. Для этого была подобрана следующая передаточная функция корректирующего устройства:

Руководствуясь данными из Рис 2.7.7 взяты приближённые коэффициенты, а затем, методом подбора они были уточнены.

Рис. 2.7.7.

Здесь время возрастания тока почти такое же как при использовании добавочного сопротивления 810 мкс. Чего по прежнему недостаточно. Далее приведены временные графики возрастания тока, и управляющие сигналы, что даёт наглядное представление того, как работает корректирующие устройство:

Рис. 2.7.8.

Корректирующее устройство проще всего реализовать в микроконтроллере. Кроме того цифровая или дискретная коррекция весьма интересна с практической точки зрения в силу конструктивной универсальности устройств и гибкости настройки. Чтобы перейти от непрерывной ПФ корректирующего устройства W_к(s) к эквивалентной дискретной W_к(z) необходимо сделать замену:

где: T_ц - период выполнения программы касательно корректирующего устройства.

В результате получим следующую передаточную функцию:

(22)

Чтобы зашить эту функцию в микроконтроллере, нужно реализовать в нём следующий алгоритм (Рис 2.7.9), выполнение которого займёт около 50-ти тактов работы микроконтроллера.

Рис. 2.7.9.

Но как было выше сказано время возрастания/спада не удовлетворяет требованиям к системе, поэтому нужно искать другие, более эффективные методы решения этой задачи.

Использование форсирующего импульса.

В начале каждого шага подаётся 100% - шим того или иного знака, иначе говоря форсирующий импульс, который приводит к быстрому изменению тока. Здесь важно точно рассчитать длительность этого импульса, потому что, если он превысит допустимые пределы ток может вырасти выше номинального в несколько раз, что приведёт к перегоранию обмоток.

Выведем формулу для расчета длительности форсирующего импульса от напряжения питания (U = 24 в) и от тока, который следует получить в результате. В самом общем случае, это не ток, а разность токов между нынешним и будущим током после воздействия импульса. Поэтому обозначим его dI, чтобы подчеркнуть что эта переменная может использоваться как разница токов.

Начнём вывод с общеизвестной функции тока от времени в катушке индуктивности при подключении к источнику напряжения:

(23)

Далее выводим из формулы время t:

(24)

Вносим полученную формулу и m-файл и реализуем метод на математической модели.

Tf = L*log(U/(U-Inom*(Rd+r)))/(Rd+r)

%время форсирующего импульса [с]

Рис. 2.7.9.

В модели на Рис. 2.7.9 блок FORS формирует форсирующий импульс, требуемой длины. И далее этот сигнал поступает на драйвер. Результаты полученные в результате моделирования:

Рис. 2.7.10.

Здесь сигнал, который называется – управляющий сигнал на выходе корректирующего устройства назван так, потому что формирователь форсирующего звена по сути и есть корректирующее звено. Оно может находиться в микроконтроллере в виде затабулированной таблицы. В ней указанны длительности форсирующих импульсов для каждого такта. В результате (см. Рис 2.7.10.) Получаем время нарастания тока 296 мкс, что более чем в 2 раза выше требуемой величины и в несколько раз превышает раннее полученные результаты.

В этой главе было проделано большое количество анализов для различный методов форсирования токов, подведём итоги:

Выводы по выбору способов форсирования токов.

Осветим численные результаты для различных методов. В качестве тестовой задачи требуется увеличить ток в обмотке ШД с нуля до Inom = 2.8 А, имея в наличии источник напряжения 24 в.

1. Без коррекции. Время нарастания тока: 7121 мкс.

2. С использованием добавочного сопротивления. Время нарастания тока: 870 мкс. Недостатком метода являются большие тепловые потери: 120 Вт для одного двигателя.

3. С использованием корректирующего устройства в виде передаточной функции. Время нарастания тока: 810 мкс. Недостатки метода: высокая загруженность микроконтроллера.

4. С использованием форсирующего импульса напряжения. Время нарастания тока: 296 мкс. Явных недостатков нет.

Из предложенных методов только последний показал удовлетворительные результаты: время нарастания 296 мкс. по сравнению с требуемым значением 780 мкс.

Реализация метода форсирующих импульсов в микрошаге (MATLAB).

В микрошаговом режиме существуют переходы между уровнями токов, но они меньше чем в полношаговом режиме. Например для выбранного ¼-шагового режима самый большой переход равен 0.39*Inom. Поэтому и форсирующие импульсы будут заметно меньше. Микроконтроллер способен очень быстро извлекать данные из стека (около 2 МГц), поэтому длительность импульсов можно задать с точностью 0.5 мкс.

Для каждого такта (а их 16) требуется вычислить длительность импульса. Если это делать в MATLAB потребуется 2 матрицы:

1. Ms(16,4) – амлитудные точки: для каждого такта их 4.

2. Mt(16,4) – временные точки: для каждого такта их также 4.

Освещаем алгоритм вычисления точек:

Ms=ones(16,4);

Mt=ones(16,4);

for i=1:16

Ms(i,1)=1;

Ms(i,2)=1;

Ms(i,3)=Kd*sin((i-1)*pi/8);

Ms(i,4)=Kd*sin((i-1)*pi/8);

if i>1

if Ms(i,3)>Ms(i-1,3)

Ms(i,1)=1;

Ms(i,2)=1;

else

Ms(i,1)=-1;

Ms(i,2)=-1;

end;

else

Ms(i,1)=1;

Ms(i,2)=1;

end;

t1=L*log(1/(1-(sin((i-2)*pi/8)-sin((i-1)*pi/8))*Kd))/(Rd+r)

t1=abs(t1);

Mt(i,1)=(i-1)*Tt+Tvt;

Mt(i,2)=(i-1)*Tt+t1;

Mt(i,3)=(i-1)*Tt+t1+Tvt;

Mt(i,4)=i*Tt;

end;

В результате получаем числовую матрицу точек, готовых для занесения в стек микроконтроллера. Но для этого конечно их нужно привести к соответствующему базису, но об этом позже.

Таблица: “точки для форсирующих импульсов”

Ms =

1.0000 1.0000 0 0

1.0000 1.0000 0.0491 0.0491

1.0000 1.0000 0.0907 0.0907

1.0000 1.0000 0.1186 0.1186

1.0000 1.0000 0.1283 0.1283

-1.0000 -1.0000 0.1186 0.1186

-1.0000 -1.0000 0.0907 0.0907

-1.0000 -1.0000 0.0491 0.0491

-1.0000 -1.0000 0.0000 0.0000

-1.0000 -1.0000 -0.0491 -0.0491

-1.0000 -1.0000 -0.0907 -0.0907

-1.0000 -1.0000 -0.1186 -0.1186

-1.0000 -1.0000 -0.1283 -0.1283

1.0000 1.0000 -0.1186 -0.1186

1.0000 1.0000 -0.0907 -0.0907

1.0000 1.0000 -0.0491 -0.0491

Mt =

0.0000 0.0001 0.0001 0.0042

0.0042 0.0043 0.0043 0.0083

0.0083 0.0084 0.0084 0.0125

0.0125 0.0126 0.0126 0.0167

0.0167 0.0167 0.0167 0.0208

0.0208 0.0209 0.0209 0.0250

0.0250 0.0251 0.0251 0.0292

0.0292 0.0293 0.0293 0.0333

0.0333 0.0334 0.0334 0.0375

0.0375 0.0376 0.0376 0.0417

0.0417 0.0418 0.0418 0.0458

0.0458 0.0459 0.0459 0.0500

0.0500 0.0500 0.0500 0.0542

0.0542 0.0542 0.0542 0.0583

0.0583 0.0584 0.0584 0.0625

0.0625 0.0626 0.0626 0.0667

В MATLAB используем блок Repeating Sequence Interpolated1. В нем есть специальные поля для массивов имплитудных и отдельно для временных точек. Заносим туда данные из выше выведенной таблицы, и получаем:

Рис. 2.7.11.

Это управляющий сигнал для обмотки A, аналогичным образом строиться сигнал для обмотки B с той разницей что он сдвинут по фазе на 90 градусов. Теперь блок микроконтроллера пополнился корректирующим устройством:

Рис. 2.7.12.

Для анализа данных будем использовать общую модель всей системы, где задействованные все устройства:

Рис. 2.7.12.

Сейчас нас интересуют следующие осциллографы: control signal (управляющие сигналы), pwm signal (сигнал ШИМ-а с драйвера) и current (ток в обмотках).

Требуемая скорость по техническому заданию составляет 70 мм/сек, что в переводе примерно равно 300 шагам в секунду. Сравним графики токов с форсированием и без него, на этой скорости. (см. на чертеже). Видно что без форсирования ток отстаёт по фазе на примерно 30 градусов, при этом ошибка может составлять до 50% от требуемой величины. С применением форсирующего импульса ошибка не превышает 5% - что вполне допустимо.