
Лабораторная работа 119
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВНУТРЕННЕГО ТРЕНИЯ
ЖИДКОСТИ ПО МЕТОДУ СТОКСА
Цель работы: ознакомиться с понятием внутреннего трения и с теорией метода (см. введение); измерить коэффициент вязкости касторового масла.
Приборы и принадлежности: стеклянный цилиндр на подставке; микрометр; секундомер; миллиметровая линейка; шарики.
Описание установки
и методики измерений.
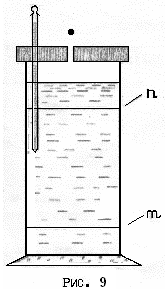
Экспериментальная установка состоит
из широкого стеклянного цилиндра
(рис.9), наполненного касторовым маслом.
Сверху цилиндр закрывается крышкой, в
центре которой имеется отверстие для
опускания шариков в исследуемую жидкость.
На цилиндре имеются две кольцевые
горизонтальные метки
![]() ,
расположенные друг от друга на расстоянииl.
Верхняя метка нанесена на том месте,
где движение шарика становится равномерным
(примерно на 5-8 см ниже уровня жидкости).
Диаметры шариков измеряются микрометром,
расстояние между метками – линейкой.
Время падения шарика измеряется с
помощью секундомера. Температура
жидкости измеряется термометром,
опущенным в жидкость через отверстие
в крышке.
,
расположенные друг от друга на расстоянииl.
Верхняя метка нанесена на том месте,
где движение шарика становится равномерным
(примерно на 5-8 см ниже уровня жидкости).
Диаметры шариков измеряются микрометром,
расстояние между метками – линейкой.
Время падения шарика измеряется с
помощью секундомера. Температура
жидкости измеряется термометром,
опущенным в жидкость через отверстие
в крышке.
Скорость шарика
в формуле 5 определяется из закона
равномерного движения
![]() .
Если заменить радиус на диаметр шарикаd,
то формула
.
Если заменить радиус на диаметр шарикаd,
то формула
(5) примет более удобный вид
![]() (5)
(5)
Измерения и обработка результатов измерения
1. Ознакомиться с методикой измерения микрометром.
2. С помощью микрометра измерить диаметры трех шариков. Диаметр каждого шарика измерить три раза в трех различных направлениях (винт микрометра закручивать без усилия!)
3. Опустить шарики через отверстие в крышке цилиндра и секундомером измерить время движения t каждого шарика между метками.
4. Измерить расстояние между метками.
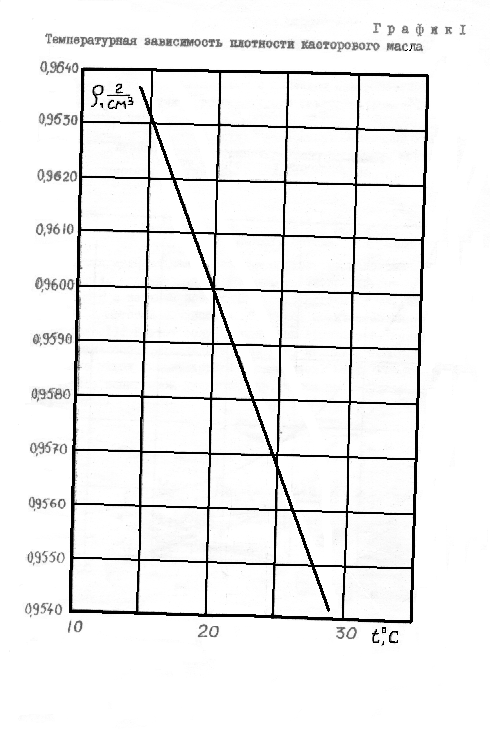
5. По графику I (см. приложение) определить плотность касторового масла при температуре опыта. Плотность материала шарика 10,96 г/см3.
6. Рассчитать из результатов каждого опыта коэффициент динамической вязкости касторового масла в пуазах.
7. Результаты измерений и вычислений занести в таблицу.
Таблица
|
№ шарика |
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
1 2 3 dср |
|
|
|
|
|
|
|
|
2 |
1 2 3 dср |
|
|
|
|
|
|
|
|
3 |
1 2 3 dср |
|
|
|
|
|
|
|
Оценить погрешность определения вязкости:
а) найти среднее
арифметическое значение
![]() ;
;
б) найти погрешности отдельных измерений
![]() ;
;
в) определить среднюю квадратичную погрешность среднего значения
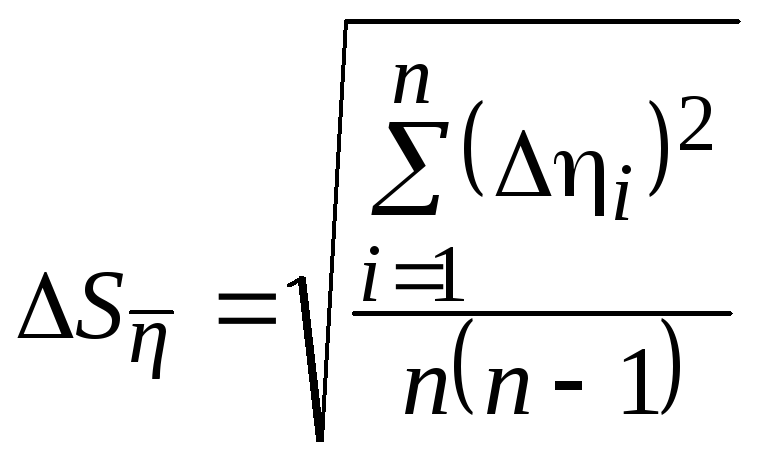 ;
;
г) задаться
доверительной вероятностью
![]() (например, 0,95);
(например, 0,95);
д) по числу измерений
и величине доверительной вероятности
определить коэффициент Стьюдента
![]() ;
;
е) найти границы доверительного интервала
![]() ;
;
ж) окончательный результат записать в виде
![]() ;
;
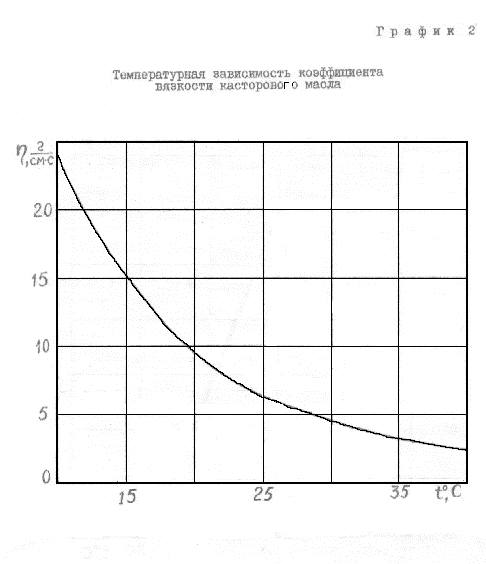
з) сравнить найденное
значение
![]() со значением
со значением![]() ,
найденным из графика 2 (см. приложение).
,
найденным из графика 2 (см. приложение).
Контрольные вопросы
Что называется коэффициентом динамической вязкости? Каков его физический смысл? В каких единицах он измеряется?
В чем состоит сущность метода Стокса?
Как изменяется скорость движения шарика с увеличением его диметра?
Почему формула Стокса справедлива при медленном равномерном движении шарика в безграничной среде? Что означает «безграничная среда»?
Литература
[1, с.218-220]; [2, с.296-297]; [3, с.143-145]; [4, с.149-152]; [5, c.138-139].
П р и л о ж е н и е
Микрометрический винт. Микрометр
Микрометрический винт применяется в точных измерительных приборах (в микрометре, микроскопе) и позволяет произвести измерения до сотых долей миллиметра. Он представляет собой стержень, снабженный винтовой нарезкой. Высота подъема винтовой нарезки на один оборот называется шагом микрометрического винта.
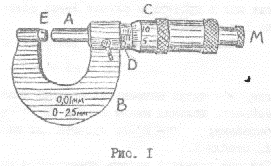
Микрометр (рис.1 и 2) состоит из двух основных частей: скобы В и микро-
метрического винта А. Микрометрический винт А проходит через отверстие скобы В с внутренней резьбой. Против микрометрического винта, на скобе, имеется упор Е. На нем закреплен полый цилиндр (барабан) С с делениями по окружности. При вращении микрометрического винта барабан скользит по линейной шкале, нанесенной на стебле Д.
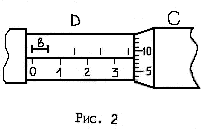
Наиболее распространен микрометр, у которого цена делений линейной шкалы стебля b равна 0,5мм. Верхние и нижние риски шкалы сдвинуты относительно друг друга на полмиллиметра: цифры проставлены только для делений нижней шкалы, то есть нижняя шкала представляет собой обычную миллиметровую шкалу (см.рис.2).
Для того, чтобы микрометрический винт А передвинулся на 1 мм, необходимо сделать два оборота барабана С. У такого микрометра на барабане С имеется шкала, содержащая 50 делений. Так как шаг винта b равен 0,5 мм, а число делений барабана т равно 50, то точность микрометра
![]() (1)
(1)
Для измерений микрометром предмет помещают между упором Е и микро-метрическим винтом А (см. рис.1) и вращают винт А за головку М до тех пор, пока измеряемый предмет не будет зажат между упором Е и концом винта А (вращение винта А производится только за головку М, так как в противном случав легко сбить совпадение нулей шкалы стебля Д и барабана С).
Числовое значение L измеряемого предмета находят по формуле
![]()
где k – число наименьших делений шкалы стебля Д; b – цена наименьшего деления шкалы стебля Д; m – число всех делений на шкале барабана; n номер отсчета по шкале С, совпадающий с осью шкалы стебля Д.
Так как в данной
работе применяется микрометр, у которого
![]() ,
то формула (1) принимает вид:
,
то формула (1) принимает вид:
![]() ,
мм
,
мм
На рис.2 отсчет по микрометру показывает
![]() .
.
ЛИТЕРАТУРА
1. Савельев И.В. Курс общей физики, т.I. М.: Наука,1970, 512 с.
2. Яворский Б.М., Детлаф А.А., Милковская Л.Б. и др. Курс физики, т,1. Высш. школа, 1965, 376 с.
3. 3исман Г.А.. Тодес 0.М.. Курс общей физики, т. I. М.: Наука. 1972. 340 с.
4.Кортнев А.В. , Рублев Ю.В., Куценко А.Н. Практикум по физике. М.: Высш.школа, 1963. 516 с.
5.Майсова Н.Н. Практикум по курсу общей физики. М.: Высш. школа, 1970, 448 с.
