№282. Диденко И. С., Гераськин В. В. Кристаллофизика

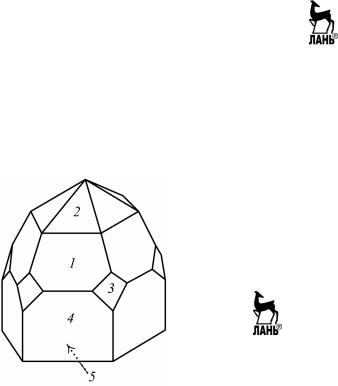
Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум

2.Спроектировать все грани кристаллического многогранника в гномостереографической проекции. Обозначить одинаковыми циф- рами грани, принадлежащие одной простой форме.

3.Выделить единичную грань (если имеется).

4.Определить соотношение a : b : c.

5.Определить по модели многогранника отрезки, отсекаемые гра- нями.

6.Определить индексы Миллера (символы) граней.

7.Определить индексы направлений, совпадающих с осями сим- метрии, и нескольких ребер, указанных преподавателем.

Пример 5.1. Кристаллический многогранник, показанный на рис. 5.9, представляет комбинацию трех гексагональных пирамид (грани 1, 2, 3), гексагональной призмы (грани 4) и моноэдра (грань 5).

Рис. 5.9. Многогранник гексагональной сингонии

Перпендикулярно моноэдру, через его середину проходит ось симметрии 6. Имеются шесть вертикальных плоскостей симметрии, которые проходят через ребра или середины граней гексагональной призмы. Формула симметрии многогранника L66Р, интернациональ- ный символ точечной группы симметрии многогранника 6mm.

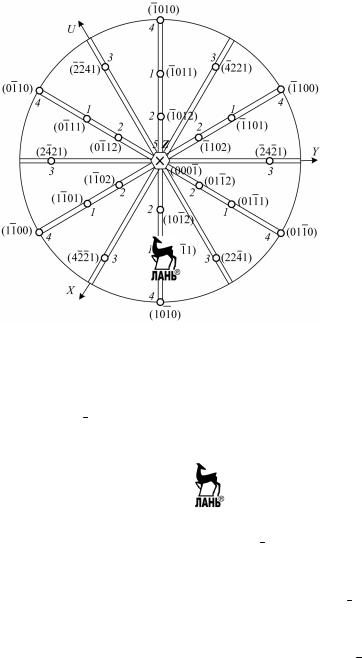
За ось Z принимается единственное единичное направление – ось симметрии 6, а оси Х, Y и U являются нормалями к вертикальным плоскостям симметрии. Проекции элементов симметрии и граней кристалла показаны на рис. 5.10 (1, 2 и 3 – грани гексагональных пи- рамид, 4 – грани гексагональной призмы, 5 – моноэдр).

71

Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум

Рис. 5.10. Стереографическая проекция элементов симметрии и гномостереографическая проекция граней многогранника, представленного на рис. 5.9

Если принять за единичную грань гексагональной призмы 1, то

индексы ее будут {0111} , так как они параллельны одной горизон-

тальной оси, а по всем остальным координатным осям отсекают еди- ничные параметры. Грани пирамиды 2 отсекают по оси Z отрезок более короткий, чем единичная грань, следовательно, четвертый индекс должен быть больше. Если, например, после параллельного переноса грани 2 и 1 отсекают одинаковые отрезки по осям Y и U, а отрезок, отсекаемый единичной гранью, в два раза больше отрезка,

отсекаемого гранью 2, то индексы граней 2 – {0112} . Так как грани

гексагональной призмы 4 вертикальны (четвертый индекс равен ну- лю) и их проекции лежат на стереографической проекции вертикаль-

ной плоскости вместе с гранями 1 и 2, то индексы граней 1 – {0110} .

Если грани пирамиды 3 (грани более вертикальные, чем единич- ная грань) после параллельного переноса будут отсекать по коорди-

натным осям отрезки а, а, – а/2, 2с, то индексы граней 3 – {2241} .

72

Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум

Горизонтальная грань 5 имеет индексы (0001) , так как она парал-

лельна осям Х, Y и U.

Ось симметрии шестого порядка совпадает с направлением оси Z и ее индекс [0001] Вертикальные ребра призмы 4 совпадают с на- правлением оси Z и индексы [0001], а горизонтальные ребра мно- гогранника, являющиеся пересечением граней призмы 4 и моноэд- ра 5, совпадают с направлением осей Х, Y и U и их индексы –

< 1010 > .

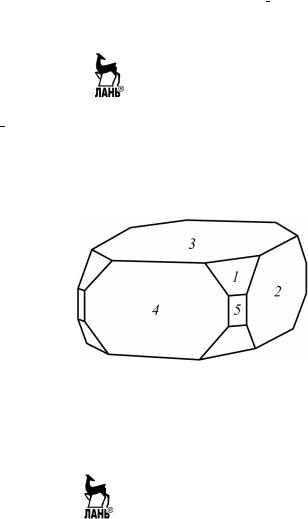
Пример 5.2. Многогранник ромбической сингонии, показанный на рис. 5.11, представляет собой комбинацию ромбической дипира- миды 1, ромбической призмы 5 и трех пинакоидов – 2, 3, 4.

Рис. 5.11. Многогранник ромбической сингонии

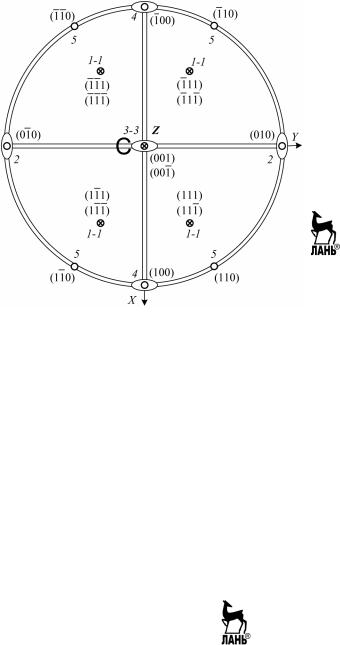
Перпендикулярно граням пинакоидов (через их середины) прохо- дят оси симметрии второго порядка, которые принимаются за на- правления осей координат. Через середины граней пинакоидов про- ходят три взаимно перпендикулярных плоскости симметрии (коор- динатные плоскости У многогранника есть центр симметрии С. Формула симметрии многогранника 3L23РС, интернациональный символ mmm. Проекция элементов симметрии и граней кристалла показаны на рис. 5.12 (1 – грани ромбической дипирамиды, 5 – грани ромбической призмы, 2, 3 и 4 – грани пинакоидов).

Если принять за единичную грань ромбической дипирамиды 1, то ее индексы – {111}. Грани ромбической призмы 5 вертикальны и от- секают по осям X и Y отрезки, прямо пропорциональные отрезкам, отсекаемым единичной гранью, и, следовательно, их индексы {110}. Грани пинакоидов 2, 3 и 4 параллельны двум координатным осям и их индексы – {100}.

73

Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум

Рис. 5.12. Стереографическая проекция элементов симметрии и гномостереографическая проекция граней многогранника, представленного на рис. 5.11

Оси второго порядка имеют индексы <100>, так как совпадают с координатными осями. Ребра многогранника, образованные пересе- чением граней пинакоидов с гранями ромбической призмы, совпа- дают с направлениями осей координат и имеют индексы <100>. Рeбpa многогранника, образованные пересечением граней ромбиче- ской дипирамиды с другими гранями кристалла, лежат в координат- ных плоскостях и имеют индексы <110>, так как эти направления параллельны линиям пересечения единичной грани с координатными плоскостями.

5.5. Требования к отчету

Отчет о работе должен содержать:

1)учебный и международный символы симметрии многогранников;

2)стереографическую проекцию элементов симметрии много- гранников;

3)гномостереографическую проекцию граней многогранников с выделением граней, принадлежащих одной простой форме;

74

Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум

4) индексы Миллера (символы) граней многогранника и символы нескольких ребер многогранника, указанных преподавателем.

Литература

К.М. Розин, В.С. Петраков. Кристаллография и кристаллохимия. Раздел: Индицирование плоскостей и направлений в кристаллах. Учеб. пособие. – М.: МИСиС, 2001. – 88 с.

Розин К.М., Петраков В.С. Кристаллофизика: Учеб. пособие. –

М.: МИСиС, 2006. – 249 с.

Розин К.М. Практическая кристаллография. – М.: МИСиС, 2005. – 487 с.

Контрольные вопросы

1.Как определить индекс Миллера грани?

2.Каково соотношение единичных параметров у кристаллов ром- бической сингонии?

3.Каково соотношение единичных параметров у кристаллов тет- рагональной сингонии?

4.Где расположена гномостереографическая проекция единичной грани тетрагонального кристалла?

5.Какие индексы может иметь единичная грань гексагонального кристалла?

6.Где расположена гномостереографическая проекция единичной грани ромбического кристалла?

7.Каково соотношение единичных параметров у кристаллов гек- сагональной сингонии?

8.С какой целью вводится четвертая ось (U) в кристаллографиче- скую систему координат для кристаллов тригональной и гексаго- нальной сингоний?

9.Записать символ горизонтальной грани тетрагонального кристалла.

10.Каким свойством обладает «четырехиндексный» символ кри- сталлов гексагональной и тригональной сингоний?

11.Определить символ грани кубического кристалла, если нормаль к

ней составляет с координатными осями углы: λ = 42,03°; μ = 68,20°;

ν= 56,15°.

12.Определить углы λ, μ, ν между нормалью к грани (110) и ося- ми координат в кристалле симметрии mm2, соотношение единичных

75

Диденко И.С., Гераськин В.В. Диденко И.С., Гераськин В.В. — Кристаллофизика. Симметрия кристаллических многогранников. Лабораторный практикум

Учебное издание

Диденко Ирина Сергеевна Гераськин Валерий Васильевич

КРИСТАЛЛОФИЗИКА

Симметрия кристаллических многогранников

Лабораторный практикум

Редактор И.Е. Оратовская

Компьютерная верстка М.А. Шамариной

Национальный исследовательский технологический университет «МИСиС», 119049, Москва, Ленинский пр-т, 4

Издательский Дом МИСиС, 119049, Москва, Ленинский пр-т, 4

Тел. (495) 638-45-22

Отпечатано в типографии Издательского Дома МИСиС 119049, Москва, Ленинский пр-т, 4

Тел. (499) 236-76-17, тел./факс (499) 236-76-35

76